Интенсивность поступающей нагрузки

113. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (2-ая формула Эрланга) предполагает, что коммутационная схема:

Однозвенная

114. Вероятность потерь в графе, состоящем из α параллельно включенных дуг, при вероятности занятости i-ой дуги wi определяется по следующей формуле:

Правильный ответ:

115. В соответствии с методом вероятностных графов функция потерь для двухзвенной схемы в режиме линейного искания запишется в виде следующей формулы:

*

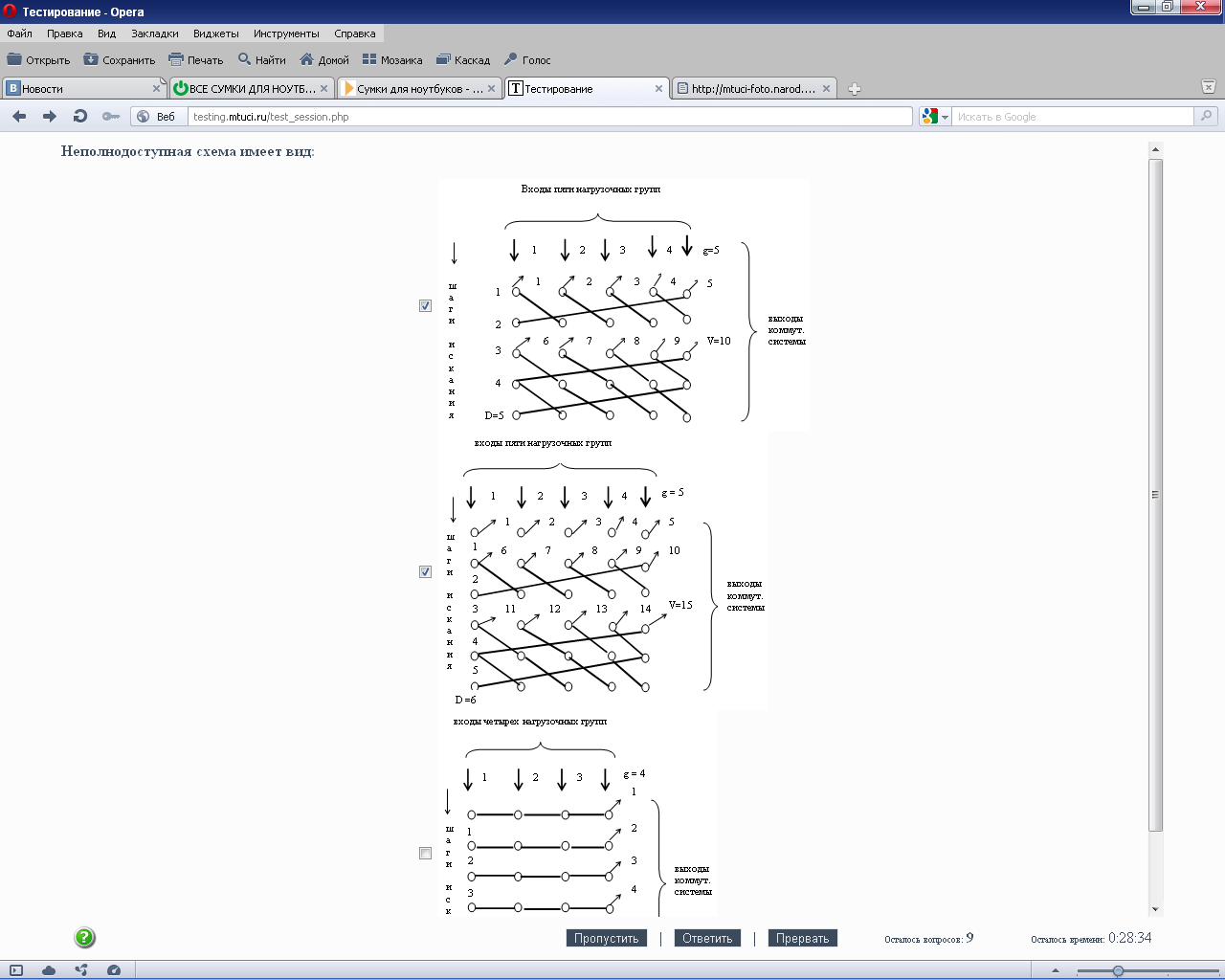
116.Неполнодоступная схема имеет вид:

117. Запись функции потерь по методу вероятностных графов в параллельно-последовательном графе сводится к умножению и суммированию вероятностей занятости отдельных дуг графа. При этом в случае параллельного включения нескольких дуг, образующих общую ветвь, вероятность занятия всей ветви вычисляется:

Произведением вероятностей занятия отдельных дуг

118. Потери в двухзвенной схеме могут возникать в следующих трех случаях:

-возникают неудачные комбинации свободных промежуточных линий и свободных выходов, которые могут быть использованы для поступающего вызова

-заняты все промежуточные линии, которые могут быть использованы для поступающего вызова

-заняты все линии в требуемом направлении искания

119. Таблицы формулы Энгсета (таблицы Лившица и Фидлина), устанавливающие соответствие между величиной интенсивности нагрузки от одного источника α, числом источников нагрузки N, емкостью пучка линий V и величиной потерь по вызовам, на практике можно пользоваться при числе источников нагрузки N:

N < 100

120. В соответствии с методом эффективной доступности математическое ожидание доступности определяется из выражения:

Интенсивность нагрузки, обслуженной mА выходами одного коммутатора звена А

121. Вероятность потерь для графа, содержащего α параллельно включенных дуг, каждая из которых содержит s последовательно включенных дуг, при вероятности занятости i-ой дуги wi запишется в виде следующей формулы:

Правильный ответ

122. Системой распределения информации может быть:

Ступень искания

123. Таблицы Пальма, устанавливающие соответствие между интенсивностью поступающей нагрузки, числом обслуживающих устройств и качеством обслуживания рассчитаны при условии выполнения следующих условий:

Дисциплина обслуживания - с потерями

Способ включения линий на выходе КС - полнодоступное

Поток вызовов - простейший

Коммутационная схема (КС) – однозвенная

124. Приближенная формула Пальма – Якобеуса для расчета потерь Р в неполнодоступном однозвенном включении линий на выходе коммутационной схемы имеет вид:

Y - интенсивность поступающей нагрузки

P - потери

D – доступность

EV-D (Y) - величина потерь в полнодоступном пучке емкостью V-D линий

Ev (Y) - величина потерь в полнодоступном пучке емкостью V линий

125. Вероятностный граф двухзвенной схемы в режиме свободного искания имеет вид:

Правильный ответ

126. Вероятностный граф двухзвенной схемы в режиме группового искания имеет вид:

Правильный ответ

127. Выражения для расчета потерь Р в двухзвенной схеме при полнодоступном включении линий в выходы коммутационной системы (основное уравнение Якобеуса) записывается в виде:

– вероятность занятия i любых промежуточных линий;

- вероятность занятия mA-i…………выходов;

Фиксированных

128. Выражения для расчета потерь Р в двухзвенной схеме при полнодоступном включении линий в выходы коммутационной системы (основное уравнение Якобеуса) записывается в виде:

– вероятность занятия i ………. промежуточных линий;

- вероятность занятия mA-i фиксированных выходов;

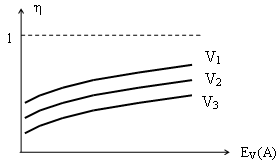
Любых

129. Системой распределения информации может быть:

Совокупность коммутационных приборов

130. Распределение Эрланга для оценки вероятности занятия i любых линий из записывается в виде:

Правильный ответ

131. Первая формула Эрланга табулирована (таблицы Пальма). С помощью этих таблиц по заданным величинам интенсивности поступающей нагрузки А и потерь EV(А) можно непосредственно определить:

Число линий

132. Хараутер зависимости средней интенсивности нагрузки η, обслуженной одной линией полнодоступного пучка от величины потерь EV(А) при различных значениях V имеет вид:

При этом:

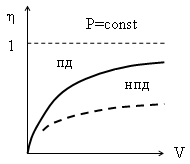
V1 < V2 < V3

133. Сравнение зависимости среднего использования одной линии полнодоступного и неполнодоступного пучков от емкости пучка при фиксированных потерях имеет вид:

134. Полнодоступным называется такое включение, при котором: