Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Любой вход коммутационной системы может быть подключен к любому выходуСодержание книги
Поиск на нашем сайте
135. Метод эффективной доступности для расчета двухзвенных неполнодоступных схем основан на понятии переменной доступности.
Если обозначить через i – число промежуточных линий из одного коммутатора звена А, занятых в рассматриваемый момент времени, то мгновенная доступности Di в рассматриваемом направлении искания определится: Di = (mA – i)q 136. Распределение Эрланга для систем с ожиданием имеет вид:
Где Рi - вероятность занятия …….. линий из общего пучка …….. при интенсивности поступающей нагрузки …….. I,V,A 137. На приведенных неполнодоступных схемах доступность D соответственно равна:
138. В соответствии с методом вероятностных графов после построения вероятностного графа дальнейшая процедура метода заключается в записи функции потерь, аргументом которой является: Вероятность занятия отдельных дуг графа 139. Вероятность потерь в графе, состоящем из s последовательно включенных дуг, при вероятности занятости i-ой дуги wi определяется по следующей формуле:
Правильный ответ 140. Таблицы Пальма позволяют определить по заданной величине интенсивности нагрузки А и емкости пучка V линий величину потерь, которая рассчитана по: Первой формуле Эрланга 141. В соответствии с методом эффективной доступности двухзвенную схему заменяют однозвенной с эффективной доступностью Dэфф, которая определяется из выражения:
Математическое ожидание доступности 142. Зависимости емкости пучка линий V от величины нагрузки А=Na от N источников при обслуживании примитивного и простейшего потоков однозвенной коммутационной схемой с потерями имеют следующий вид: Правильный ответ:
143. График зависимости числа линий V, включенных неполнодоступно в выходы однозвенной коммутационной схемы, от интенсивности поступающей нагрузки Y при фиксированных значениях потерь Р и доступности D имеет вид:
144. В соответствии с методом эффективной доступности после определения значения эффективной доступности Dэфф расчет числа линий проводится по выражению
где α и β – коэффициенты, значения которых зависят от: Структурных параметров блока 145. Разницу между поступающей и обслуженной нагрузками называют: Потерянной нагрузкой 146. График зависимости среднего использования одной линии неполнодоступного пучка η от емкости пучка V при фиксированном значении потерь Р имеет вид:
При этом: D1>D2>D3 147. Вероятностный граф двухзвенной схемы в режиме линейного искания имеет вид: Правильный ответ:
148. В основном уравнении Якобеуса экспоненциальное (Маркова) 149. Для систем с ожиданием закон распределения времени ожидания имеет вид:
t– допустимое время ожидания, которое нормируется относительно: Средней длительности занятия 150. Математическая модель метода Якобеуса для оценки пропускной способности двухзвенной коммутационной схемы, в выходы которой включен полнодоступный пучок линий, включает в себя следующие элементы: В коммутационной схеме входы и выходы Соединяются: в двух точках коммутации Поток вызовов: простейший Дисциплина обслуживания: с потерями 151. График зависимости числа линий V, включенных неполнодоступно в выходы однозвенной коммутационной схемы, от интенсивности поступающей нагрузки Y при фиксированном значении потерь Р имеет вид:
При этом: D1 < D2 < D3 152. Характер графических зависимостей числа линий V от интенсивности нагрузки А при фиксированной величине потерь Р при обслуживании простейшего потока полнодоступной однозвенной схемой по системе с явными потерями имеет вид:
153. Стационарный, ординарный поток вызовов от группы источников N < 100 является потоком: С простым последействием 154. Если N-число источников нагрузки,
155. Для характеристики систем с ожиданием используются следующие показатели:
156. Характер зависимости средней интенсивности нагрузки
При увеличении емкости пучка линий увеличивается интенсивность нагрузки, обслуженная одной линией пучка. При этом эффект от объединения пучков линий тем выше, чем: Меньше их емкость 156. Хатактер зависимости средней интенсивности нагрузки
Из графиков можно сделать вывод, что для повышения η необходимо: -увеличивать емкость пучка V 157. При построении коммутационного графа рассматривается модель коммутационной схемы, в которой вершины графа соответствуют... схемы, а дуги графа –.... Коммутаторам
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.208.127 (0.008 с.) |



 D=4
D=4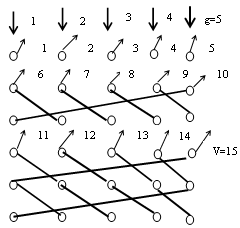 D=6
D=6 D=5
D=5








 для расчета вероятности потерь в двухзвенной схеме при полнодоступном включении выходов принято использовать распределения:
для расчета вероятности потерь в двухзвенной схеме при полнодоступном включении выходов принято использовать распределения:


 - среднее число вызовов, поступающих от одного источника за час,
- среднее число вызовов, поступающих от одного источника за час,  - средняя длительность обслуживания одного вызова, то интенсивность поступающей нагрузки A определяется по формуле:
- средняя длительность обслуживания одного вызова, то интенсивность поступающей нагрузки A определяется по формуле: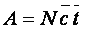
 среднее время ожидания по отношению ко всем поступившим вызовам
среднее время ожидания по отношению ко всем поступившим вызовам среднее время ожидания для задержанных в обслуживании вызовов
среднее время ожидания для задержанных в обслуживании вызовов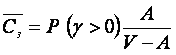 средняя длина очереди или число задержанных в обслуживании вызовов
средняя длина очереди или число задержанных в обслуживании вызовов вероятность наличия в очереди хотя бы одного вызова
вероятность наличия в очереди хотя бы одного вызова , обслуженной одной линией полнодоступного пучка, от емкости пучка V при фиксированных значениях EV(А) имеет вид:
, обслуженной одной линией полнодоступного пучка, от емкости пучка V при фиксированных значениях EV(А) имеет вид: