
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число обслуживающих устройствСодержание книги
Поиск на нашем сайте Допустимое время ожидания. 39. Зависимости ёмкости пучка линий V от величины нагрузки A=Na от N источников при обслуживании примитивного и простейшего потоков однозвенной коммутационной схемой с потерями имеют следующий вид: - Где 3 графика, простейший с пунктиром выше 40. Формула Энгсета, позволяющая определить вероятность того, что в произвольный момент времени в полнодоступном пучке емкостью V линий, на который поступает поток от ограниченного числа источников N с параметром α от одного источника, на практике применяется при числе источников: N < 100 41. Закон распределения промежутка между моментами поступления вызовов случайного потока имеет вид:
42. Зависимость вероятности ожидания p(y>t) сверх допустимого времени ожидания при постоянном времени обслуживания, при фиксированном числе обслуживающих устройств и удельной нагрузке на одно обслуживающее устройство имеет вид:
При этом V: Число обслуживающих устройств 43. Зависимость коэффициента a, учитывающего вызовы, не закончившиеся разговором, от времени чистого разговора T и доли вызовов, закончившиеся разговором kp, имеет вид:
При этом: -Kp1<Kp2<Kp3 44. За единицу измерения нагрузки принимается: - 1 часо-занятие 45. За единицу измерения интенсивности нагрузки принимается: - 1 Эрланг 46.Интенсивность поступающей нагрузки, выраженная в Эрлангах, количественно равна среднему числу вызовов, поступающих за: - время средней длительности 1 занятия 47. Интенсивность обслуженной нагрузки, выраженная в Эрлангах, количественно равна: - среднему времени обслуживания всех вызовов 48. Интенсивность случайного потока вызовов характеризует.....поступающих вызовов. - Число 49. Источники нагрузки подразделяются на следующей категории в зависимости от: -среднего числа вызовов, поступающих в час наибольшей нагрузки 50. Интенсивностью случайного потока вызовов является.....числа вызовов, поступающих в единицу времени. - математическое ожидание 51. Интенсивность нагрузки в 1 Эрланг это непрерывное занятие одной линии в течение: - Часа 52. Качество обслуживания в системах с условными потерями(с ожиданием) характеризуется: - вероятностью ожидания сверхдопустимого времени - вероятностью ожидания 53. Качество обслуживания потока вызовов коммутационной системой оценивается величиной потерь по вызовам PB, величиной потерь по нагрузке PН и величиной потерь по времени Pt. Между этими величинами в общем случае имеет место соотношение: PН ≤ PB ≤ Pt 54. Качество обслуживания вызовов в системах с явными потерями характеризуются: Величиной потерь сообщения 55. Качество обслуживания потока вызовов коммутационной системой оценивается: - величиной потерь по нагрузке РН - величиной потерь по времени Рt - величиной потерь по вызовам РВ 56. Кривые Берке для оценки вероятности ожидания Р(j>t) сверх допустимого времени ожидания при постоянном времени обслуживания применяется, если обслуживание вызовов из очереди осуществляется: В случайном порядке 57. Кривые Кроммелина для оценки вероятности ожидания Р(j>t) сверх допустимого времени ожидания при постоянном времени обслуживания применяется, если обслуживание вызовов из очереди осуществляется: - в порядке поступления вызовов 58. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (теория Кроммелина, Берке) предполагает, что поток вызовов простейший, время обслуживания: Постоянное 59. Математическая модель теории телетрафика включает в себя следующие основные элементы:
60. Математическая модель системы обслуживания, положенная в основу формулы Энгсета, предполагает, что поток вызовов: Примитивный 61. Математическая модель системы обслуживания, положенная в основу 1-ой формулы Эрланга, предполагает, что поток вызовов: Простейший 62. Математическая модель системы обслуживания, положенная в основу 1-ой формулы Эрланга, предполагает, что коммутационная схема: С явными потерями 64. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (теория Берке) предполагает, что дисциплина обслуживания с ожиданием, вызовы из очереди обслуживаются: В случайном порядке 65. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (2-ая формула Эрланга) предполагает, что поток вызовов: Простейший 66. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (2-ая формула Эрланга) предполагает, что дисциплина обслуживания с ожиданием, вызовы по очереди обслуживаются: В порядке их поступления 67. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (2-ая формула Эрланга) предполагает, что поток вызовов простейший, время обслуживания: С ожиданием 69. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (Теория Кроммелина, Берке) предполагает, что коммутационная схема: Однозвенная 70. Математическая модель системы обслуживания полнодоступных включений в соответствии с теорией Кроммелина и Берке предполагает, что дисциплина обслуживания: С ожиданием 71. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (Теория Кроммелина, Берке) предполагает, что поток вызовов: Простейший 72. Неполнодоступная схема будем иметь меньшую чувствительность к колебанием нагрузки по нагрузочным группам, если: -сумма значений элементов матрицы по строкам и столбцам будет одинакова - с увеличением № строки и столбца матрицы численные значения ее элементов увеличиваются 73. Неполнодоступным включением называется такое включение рассматриваемых линий пучка на выходе коммутационной системы, при котором каждому входу системы: Независимость 77. Одно из правил построения равномерных неполнодоступных схем формулируется следующим образом: каждая нагрузочная группа должна иметь одинаковое число общих линий с каждой другой нагрузочной группой. Из приведенных схем это правило выполняется для схемы №…
№1 78. Основными свойствами случайного потока вызовов являются: - отсутствие последействия - ординарность - стационарность 79. Одной из характеристик неполнодоступного включения является матрица связности, в которой указывается: Строится матрица связности 84. Одной из характеристик неполнодоступного включения является матрица связности, число строк и столбцов которой равно: Числу нагрузочных групп 85. Одной из характеристик неполнодоступного включения является матрица связности, в которой указывается число общих связей между выходами каждой пары нагрузочных групп. Чтобы неполнодоступная схема имела меньшую чувствительность к колебанию нагрузки по нагрузочным группам необходимо, чтобы: - матрица связности была равномерной - сумма по строкам и столбцам одинакова 86. Одно из правил построения равномерных неполнодоступных схем формулируется следующим образом: каждая линия, вкл-я в выходы коммутационной схемы, должна быть доступна одинаковому числу нагрузочных групп (или отличаться на единицу). Из приведенных схем это правильно выполняется для схемы №…
№2 87. Отношение общего числа выходов gD неполнодоступной схемы всех нагрузочных групп g с доступностью D к числу подключаемых линий V y=gD/V называют: Все V линии 91. Под поступающей нагрузкой понимают: - нагрузку, которая была бы обслужена, если бы каждому вызову немедленно предоставлялся выход -нагрузку, поступающую на выходы КС 92. При построении ступенчатых схем с перехватом и со сдвигом неполнодоступная схема имеет: Пуассона 96. Под обслуженной нагрузкой понимают: Самое длинное)) 98. Предметом теории телетрафика является: Поток вызывающих моментов 102. Потери по вызовам – это доля вызовов от общего числа поступивших, которые не обслужены по причине: Набор номера Установление соединения Разговор Разъединение 106. Приближенная формула Пальма-Якобеуса для расчета потерь Р в неполнодоступном однозвенном включении линий на выходе коммутационной схемы имеет вид: P=Ev(Y)/Ev-d(Y) Число линий V из этой формулы может быть определено: Подбором 107. При фиксированных значениях интенсивности поступающей нагрузки А и емкости пучка линий Vмежду вероятностью условных потерь и вероятностью явных потерь выполняется соотношение: Ev(A)<P(y>0) 108. Потери по времени – это доля времени, в течение которого: Времени 110. Поток вызовов называется детерминированным, если: Однозвенная 114. Вероятность потерь в графе, состоящем из α параллельно включенных дуг, при вероятности занятости i-ой дуги wi определяется по следующей формуле:
Правильный ответ: 115. В соответствии с методом вероятностных графов функция потерь для двухзвенной схемы в режиме линейного искания запишется в виде следующей формулы:
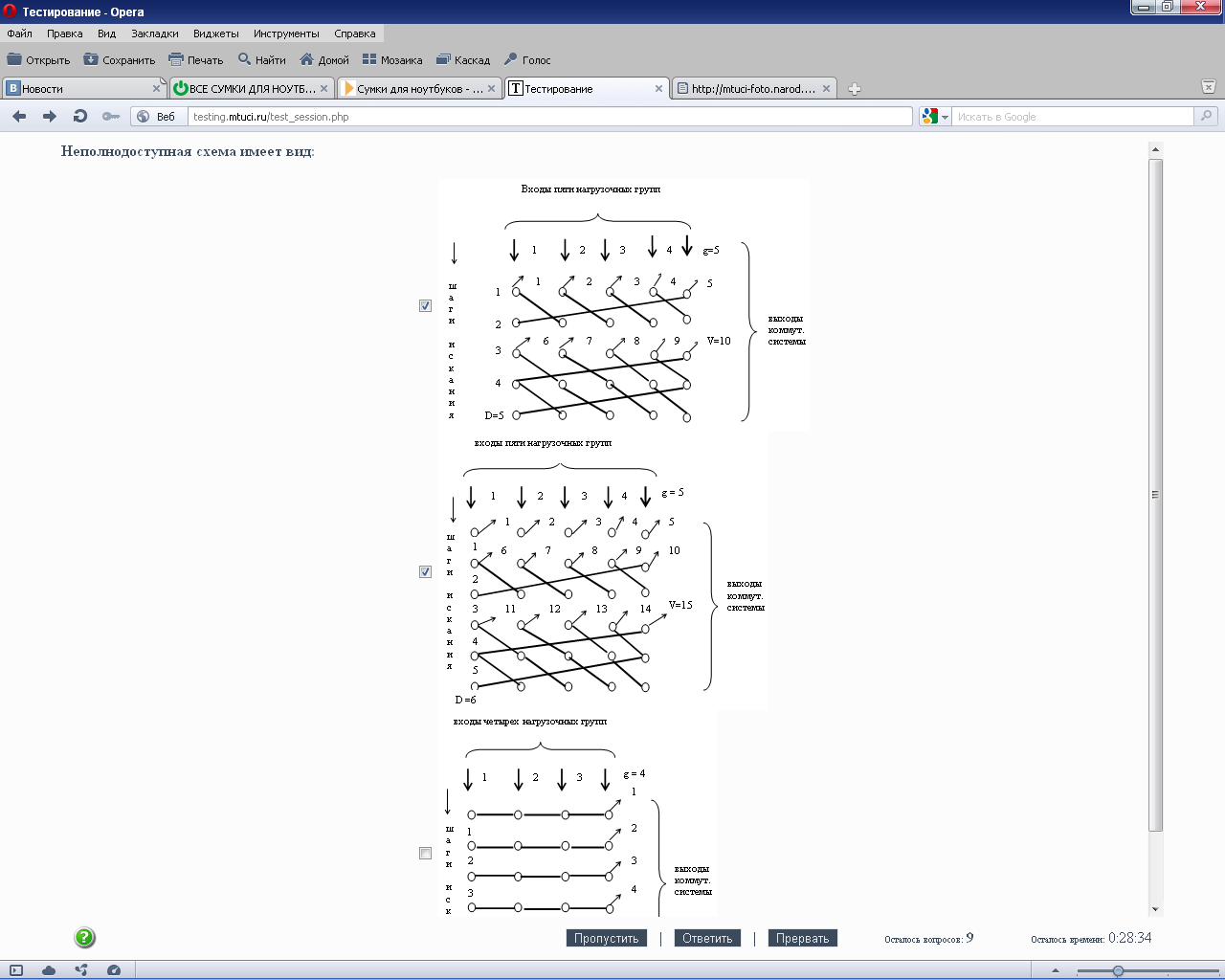
* 116.Неполнодоступная схема имеет вид:
117. Запись функции потерь по методу вероятностных графов в параллельно-последовательном графе сводится к умножению и суммированию вероятностей занятости отдельных дуг графа. При этом в случае параллельного включения нескольких дуг, образующих общую ветвь, вероятность занятия всей ветви вычисляется: Ступень искания 123. Таблицы Пальма, устанавливающие соответствие между интенсивностью поступающей нагрузки, числом обслуживающих устройств и качеством обслуживания рассчитаны при условии выполнения следующих условий: Дисциплина обслуживания - с потерями Поток вызовов - простейший P - потери D – доступность Фиксированных 128. Выражения для расчета потерь Р в двухзвенной схеме при полнодоступном включении линий в выходы коммутационной системы (основное уравнение Якобеуса) записывается в виде:
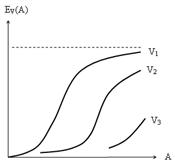
Любых 129. Системой распределения информации может быть: Число линий 132. Хараутер зависимости средней интенсивности нагрузки η, обслуженной одной линией полнодоступного пучка от величины потерь EV(А) при различных значениях V имеет вид:
V1 < V2 < V3 133. Сравнение зависимости среднего использования одной линии полнодоступного и неполнодоступного пучков от емкости пучка при фиксированных потерях имеет вид:
134. Полнодоступным называется такое включение, при котором: I,V,A 137. На приведенных неполнодоступных схемах доступность D соответственно равна:
138. В соответствии с методом вероятностных графов после построения вероятностного графа дальнейшая процедура метода заключается в записи функции потерь, аргументом которой является: Первой формуле Эрланга 141. В соответствии с методом эффективной доступности двухзвенную схему заменяют однозвенной с эффективной доступностью Dэфф, которая определяется из выражения:
Потерянной нагрузкой 146. График зависимости среднего использования одной линии неполнодоступного пучка η от емкости пучка V при фиксированном значении потерь Р имеет вид:
При этом: D1>D2>D3 147. Вероятностный граф двухзвенной схемы в режиме линейного искания имеет вид: Правильный ответ:
148. В основном уравнении Якобеуса экспоненциальное (Маркова) 149. Для систем с ожиданием закон распределения времени ожидания имеет вид:
t– допустимое время ожидания, которое нормируется относительно: Поток вызовов: простейший Дисциплина обслуживания: с потерями 151. График зависимости числа линий V, включенных неполнодоступно в выходы однозвенной коммутационной схемы, от интенсивности поступающей нагрузки Y при фиксированном значении потерь Р имеет вид:
При этом: D1 < D2 < D3 152. Характер графических зависимостей числа линий V от интенсивности нагрузки А при фиксированной величине потерь Р при обслуживании простейшего потока полнодоступной однозвенной схемой по системе с явными потерями имеет вид:
153. Стационарный, ординарный поток вызовов от группы источников N < 100 является потоком: С простым последействием 154. Если N-число источников нагрузки,
155. Для характеристики систем с ожиданием используются следующие показатели:
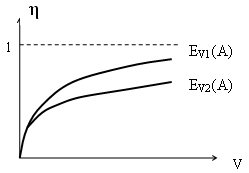
156. Характер зависимости средней интенсивности нагрузки
При увеличении емкости пучка линий увеличивается интенсивность нагрузки, обслуженная одной линией пучка. При этом эффект от объединения пучков линий тем выше, чем: Меньше их емкость 156. Хатактер зависимости средней интенсивности нагрузки
Из графиков можно сделать вывод, что для повышения η необходимо: -увеличивать емкость пучка V 157. При построении коммутационного графа рассматривается модель коммутационной схемы, в которой вершины графа соответствуют... схемы, а дуги графа –.... Коммутаторам Часам суток 159. Характер графических зависимостей числа линий V от интенсивности поступающей нагрузки А при фиксированной величине потерь Р при обслуживании простейшего потока вызовов полнодоступной однозвенной схемой по системе с потерями имеет вид:
При этом: P1 < P2 < P3 160. Выражения для расчета потерь Р в двухзвенной схеме при полнодоступном включении линий в выходы коммутационной системы (основное уравнение Якобеуса) записывается в виде:
Это выражение справедливо при выполнении следующих условий: независимость событий, описываемых вероятностями
162. Равномерным называется такое неполнодоступное включение, при котором число нагрузочных групп, обслуживаемых одной линией пучка -одинаково или отличается на единицу 163. Равномерные неполнодоступные схемы включения выходов КС применяются в -Координатных системах коммутации. 164. Средняя интенсивность нагрузки η, обслуженная одной линией полнодоступного пучка, определяется как отношение обслуженной нагрузки YO к емкости пучка V. Зависимость η от емкости пучка имеет при различных значениях EV(Y) имеет вид:
При этом: EV1(A) > EV2(A) 165. Системой распределения информации может быть: -телефонная сеть общего пользования 166. Системы, в которых поступающий вызов в момент занятости всех обслуживающих устройств теряется, называются системами: -с явными потерями 167. Стационарный, ординарный поток вызовов, параметр которого зависит от состояния системы, является потоком: -с простым последействием (примитивным или Энгсетовским) 168. Стационарный, ординарный поток вызовов от группы источников N приближается к простейшему: -с ростом N 169. Свойство стационарности случайного потока вызовов означает …. математического ожидания числа вызовов, поступающих в единицу времени. -Постоянство 170. Случайный поток задается:
171. Случайным называется такой поток вызовов, в котором: -вызовы поступают через случайные интервалы времени 172. Свойство ординарности случайного потока вызовов означает практическую невозможность появления одновременно…… и более вызовов -двух 173. Ступенчатым называется такое неполнодоступное включение при котором число нагрузочных групп, обслуживаемых одной линией пучка: -увеличивается с увеличением номера шага искания 174. Степень концентрации нагрузки оценивается коэффициентом концентрации, который определяется как отношение нагрузки за час к нагрузке за: -Сутки 175. Системы, в которых поступающий вызов в момент занятости всех обслуживающих устройств не теряется, а обслуживается с ожиданием, называются системами: -С условными потерями 176. Совокупность входов коммутационной системы, каждому из которых доступны одни и те же D линий неполнодоступного пучка, называется: -нагрузочной группой 177. Случайная функция K(t) числа вызовов, поступающих в систему за интервал времени [t0,ti], имеет вид:
178. Сравнение пропускной способности коммутационной при обслуживании примитивного и простейшего потока можно представить в виде графика зависимости потерь по вызовам РВ от числа источников нагрузки N, который имеет вид:
179. Средняя интенсивность нагрузки η, обслуженная одной линией полнодоступного пучка, определяется как отношение обслуженной нагрузки YOк емкости пучка V. Зависимость η от емкости пучка имеет вид:
180. Сравнение зависимости вероятности ожидания P(γ>t) сверх допустимого времени ожидания для систем с экспоненциальным временем обслуживания (2ая формула Эрланга) и постоянным временем обслуживания (кривые Кроммелина) можно представить в виде следующего графика.
181. Стационарный, ординарный поток вызовов от группы источника N<100 является потоком -с простым последействием 182. Сравнение зависимости вероятности ожидания P(γ>0) сверх допустимой времени по теореме Коммелина и Берке имеет вид:
183. Телефонная нагрузка это: -суммарное время занятия обслуживающих устройств 184. Теория телетрафика изучает соотношение между: -Величиной информационной нагрузки, количеством обслуживающих устройств и качество обслуживания. 185. Таблицы Пальма, устанавливающие соответствие между интенсивностью поступающей телефонной нагрузки, числом обслуживающих устройств и качеством обслуживания на практике можно пользоваться при числе источников нагрузки N: -N>-100 186. Таблицы формулы Энгсета (таблицы Лившица и Фидлина), устанавливающие соответствие между величиной интенсивности нагрузки от одного источника α, числом источников нагрузки N, емкостью пучка линии V и величиной потерь по вызовам, рассчитаны при выполнении следующих условий: -Способ включения линий на выходе КС --- полнодоступное -Поток вызовов --- примитивный -Дисциплина обслуживания --- с потерями -Коммутационная схема(КС) --- однозвенная 187. Удельная нагрузка α на одну абонентскую линию может принимать значения: -a<1 188. Формула Энгсета табулирована (таблицы Лившица и Фидлина). С помощью этих таблиц по заданной величине интенсивности нагрузки от одного источника α, числу источников нагрузки N и величине потерь по вызовам РВ можно непосредственно определить: -число линий 189. Формула Энгсета табулирована (таблицы Лившица и Фидлина). С помощью этих таблиц по заданной величине интенсивности нагрузки от одного источника α, числу линий V и величине потерь по вызовам РВ можно непосредственно определить: -число источников нагрузки 190. Формула Энгсета записывается в виде:
-V,N,a,i 192. Характер графических зависимостей числа линий V от интенсивности поступающей нагрузки А при фиксированной величине потерь Р при обслуживании простейшего потока вызовов полнодоступной однозвенной схемой по системе с потерями имеет вид: при этом -P1<P2<P3
193. Характер графических зависимостей между параметрами А, V и P, входящими в первую формулу Эрланга, имеют вид:
194. Характер зависимости коэффициента α, учитывающего вызовы, не закончившиеся разговором, от времени чистого разговора Т и доли вызовов, закончившихся разговором kр, имеет вид:
195. В системе с ожиданием вероятность того, что поступивший в формула Эрланга) выражается формулой:
-число линий 196. Математическая модель системы обслуживания, положенная в основу формулы Энгсета, предполагает, что коммутационная схема: С явными потерями 205. Величина потерь Р в неполнодоступном однозвенном включении определяется по упрощенной формуле Эрланга:
Y - интенсивность нагрузки V - число линий D - доступность 206. Простейший поток вызовов обладает следующими свойствами: -ординарностью -отсутствием последействия -стационарностью 207. Распределение Эрланга может быть записано в виде:
где V, Y, i 208. Формула Энгсета табулирована (таблицы Лившица и Фидлина). С помощью этих таблиц по заданной величине интенсивности нагрузки от одного источника α, числу источников нагрузки N и емкости пучка линий V можно непосредственно определить: Величину потерь по вызовам 209. В системе с ожиданием вероятность того, что поступивший в произвольный момент времени вызов найдет все линии занятыми, или, что то же самое, что вероятность времени ожидания будет больше нуля (2-ая формула Эрланга) выражается формулой:
Число линий 210. На практике оценка пропускной способности полнодоступного однозвенного включения по системе с потерями по 1-ой формуле Эрланга обычно принимается при числе источников нагрузки N: N ≥ 100 211. Теория телетрафика изучает соотношение между: величиной и характером информационной [1], [2] обслуживающих устройств и [3] обслуживания требований на установление соединений. В порядке их поступления 214. Качество обслуживания потока вызовов коммутационной системой оценивается величиной потерь по вызовам PB, по нагрузке PН и по времени Pt. При обслуживании простейшего потока по дисциплине с явными потерями однозвенной коммутационной схемой, в выходы которой включен полнодоступный пучок линий, имеет место соотношение: PН = PB = Pt
Допустимое время ожидания. 39. Зависимости ёмкости пучка линий V от величины нагрузки A=Na от N источников при обслуживании примитивного и простейшего потоков однозвенной коммутационной схемой с потерями имеют следующий вид: - Где 3 графика, простейший с пунктиром выше 40. Формула Энгсета, позволяющая определить вероятность того, что в произвольный момент времени в полнодоступном пучке емкостью V линий, на который поступает поток от ограниченного числа источников N с параметром α от одного источника, на практике применяется при числе источников: N < 100 41. Закон распределения промежутка между моментами поступления вызовов случайного потока имеет вид:
42. Зависимость вероятности ожидания p(y>t) сверх допустимого времени ожидания при постоянном времени обслуживания, при фиксированном числе обслуживающих устройств и удельной нагрузке на одно обслуживающее устройство имеет вид:
При этом V: Число обслуживающих устройств 43. Зависимость коэффициента a, учитывающего вызовы, не закончившиеся разговором, от времени чистого разговора T и доли вызовов, закончившиеся разговором kp, имеет вид:
При этом: -Kp1<Kp2<Kp3 44. За единицу измерения нагрузки принимается: - 1 часо-занятие 45. За единицу измерения интенсивности нагрузки принимается: - 1 Эрланг 46.Интенсивность поступающей нагрузки, выраженная в Эрлангах, количественно равна среднему числу вызовов, поступающих за: - время средней длительности 1 занятия 47. Интенсивность обслуженной нагрузки, выраженная в Эрлангах, количественно равна: - среднему времени обслуживания всех вызовов 48. Интенсивность случайного потока вызовов характеризует.....поступающих вызовов. - Число 49. Источники нагрузки подразделяются на следующей категории в зависимости от: -среднего числа вызовов, поступающих в час наибольшей нагрузки 50. Интенсивностью случайного потока вызовов является.....числа вызовов, поступающих в единицу времени. - математическое ожидание 51. Интенсивность нагрузки в 1 Эрланг это непрерывное занятие одной линии в течение: - Часа 52. Качество обслуживания в системах с условными потерями(с ожиданием) характеризуется: - вероятностью ожидания сверхдопустимого времени - вероятностью ожидания 53. Качество обслуживания потока вызовов коммутационной системой оценивается величиной потерь по вызовам PB, величиной потерь по нагрузке PН и величиной потерь по времени Pt. Между этими величинами в общем случае имеет место соотношение: PН ≤ PB ≤ Pt 54. Качество обслуживания вызовов в системах с явными потерями характеризуются: Величиной потерь сообщения 55. Качество обслуживания потока вызовов коммутационной системой оценивается: - величиной потерь по нагрузке РН - величиной потерь по времени Рt - величиной потерь по вызовам РВ 56. Кривые Берке для оценки вероятности ожидания Р(j>t) сверх допустимого времени ожидания при постоянном времени обслуживания применяется, если обслуживание вызовов из очереди осуществляется: В случайном порядке 57. Кривые Кроммелина для оценки вероятности ожидания Р(j>t) сверх допустимого времени ожидания при постоянном времени обслуживания применяется, если обслуживание вызовов из очереди осуществляется: - в порядке поступления вызовов 58. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (теория Кроммелина, Берке) предполагает, что поток вызовов простейший, время обслуживания: Постоянное 59. Математическая модель теории телетрафика включает в себя следующие основные элементы:
60. Математическая модель системы обслуживания, положенная в основу формулы Энгсета, предполагает, что поток вызовов: Примитивный 61. Математическая модель системы обслуживания, положенная в основу 1-ой формулы Эрланга, предполагает, что поток вызовов: Простейший 62. Математическая модель системы обслуживания, положенная в основу 1-ой формулы Эрланга, предполагает, что коммутационная схема:
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |












 – вероятность занятия i ………. промежуточных линий;
– вероятность занятия i ………. промежуточных линий; - вероятность занятия mA-i фиксированных выходов;
- вероятность занятия mA-i фиксированных выходов;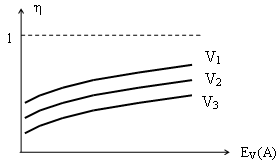 При этом:
При этом: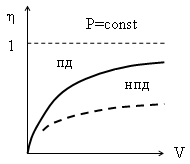
 D=4
D=4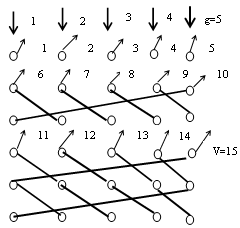 D=6
D=6 D=5
D=5



 для расчета вероятности потерь в двухзвенной схеме при полнодоступном включении выходов принято использовать распределения:
для расчета вероятности потерь в двухзвенной схеме при полнодоступном включении выходов принято использовать распределения:


 - среднее число вызовов, поступающих от одного источника за час,
- среднее число вызовов, поступающих от одного источника за час,  - средняя длительность обслуживания одного вызова, то интенсивность поступающей нагрузки A определяется по формуле:
- средняя длительность обслуживания одного вызова, то интенсивность поступающей нагрузки A определяется по формуле: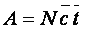
 среднее время ожидания по отношению ко всем поступившим вызовам
среднее время ожидания по отношению ко всем поступившим вызовам среднее время ожидания для задержанных в обслуживании вызовов
среднее время ожидания для задержанных в обслуживании вызовов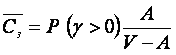 средняя длина очереди или число задержанных в обслуживании вызовов
средняя длина очереди или число задержанных в обслуживании вызовов вероятность наличия в очереди хотя бы одного вызова
вероятность наличия в очереди хотя бы одного вызова , обслуженной одной линией полнодоступного пучка, от емкости пучка V при фиксированных значениях EV(А) имеет вид:
, обслуженной одной линией полнодоступного пучка, от емкости пучка V при фиксированных значениях EV(А) имеет вид:







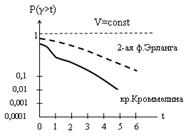

 Где Pi - это вероятность того, что в произвольный момент времени в полнодоступном пучке емкостью ………. линий, на который поступает поток от ограниченного числа источников нагрузки ……. с параметром потока……… от одного источника, занято ровно ……….. линий..
Где Pi - это вероятность того, что в произвольный момент времени в полнодоступном пучке емкостью ………. линий, на который поступает поток от ограниченного числа источников нагрузки ……. с параметром потока……… от одного источника, занято ровно ……….. линий..


 , где
, где
 - это вероятность того, что в произвольный момент времени в полнодоступном пучке емкостью…..линий, на который поступает интенсивность нагрузки …….., создаваемой простейшим потоком, занято ……любых линий.
- это вероятность того, что в произвольный момент времени в полнодоступном пучке емкостью…..линий, на который поступает интенсивность нагрузки …….., создаваемой простейшим потоком, занято ……любых линий.


