Однозвенная, в выходы которой вкл полнодоступный пучок линий, каналов

63. Математическая модель системы обслуживания, положенная в основу 1-ой формулы Эрланга, предполагает, что дисциплина обслуживания:

С явными потерями

64. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (теория Берке) предполагает, что дисциплина обслуживания с ожиданием, вызовы из очереди обслуживаются:

В случайном порядке

65. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (2-ая формула Эрланга) предполагает, что поток вызовов:

Простейший

66. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (2-ая формула Эрланга) предполагает, что дисциплина обслуживания с ожиданием, вызовы по очереди обслуживаются:

В порядке их поступления

67. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (2-ая формула Эрланга) предполагает, что поток вызовов простейший, время обслуживания:

Распределено по экспоненциальному закону

68. Математическая модель системы обслуживания полнодоступных включений по 2-ой формуле Эрланга предполагает, что дисциплина обслуживания:

С ожиданием

69. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (Теория Кроммелина, Берке) предполагает, что коммутационная схема:

Однозвенная

70. Математическая модель системы обслуживания полнодоступных включений в соответствии с теорией Кроммелина и Берке предполагает, что дисциплина обслуживания:

С ожиданием

71. Математическая модель системы обслуживания полнодоступных включений по системе с ожиданием (Теория Кроммелина, Берке) предполагает, что поток вызовов:

Простейший

72. Неполнодоступная схема будем иметь меньшую чувствительность к колебанием нагрузки по нагрузочным группам, если:

-сумма значений элементов матрицы по строкам и столбцам будет одинакова

- с увеличением № строки и столбца матрицы численные значения ее элементов увеличиваются

73. Неполнодоступным включением называется такое включение рассматриваемых линий пучка на выходе коммутационной системы, при котором каждому входу системы:

Доступна только часть линий пучка

74. Отношение общего числа выходов gD неполнодоступной схемы всех нагрузочных групп g с доступностью D к числу подключаемых линий V y=gD/V называют коэффициентом уплотнения. Неполнодоступное включением имеет место, если:

1<y<g

75. Однозвенным называется такое включение, при котором:

Вход с выходом коммутационной системы соединяется в одной точке коммутации

76. Отсутствие последействия это … вероятности поступления к вызовов в интервале времени [t0,ti) от того, сколько вызовов и как они поступали до момента t0.

Независимость

77. Одно из правил построения равномерных неполнодоступных схем формулируется следующим образом: каждая нагрузочная группа должна иметь одинаковое число общих линий с каждой другой нагрузочной группой. Из приведенных схем это правило выполняется для схемы №…

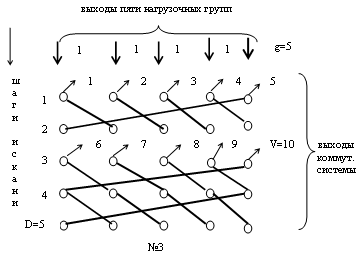
№1

78. Основными свойствами случайного потока вызовов являются:

- отсутствие последействия

- ординарность

- стационарность

79. Одной из характеристик неполнодоступного включения является матрица связности, в которой указывается:

Число общих линий между каждой парой нагрузочных групп

81. Одно из правил построения равномерных неполнодоступных схем формулируется следующим образом: каждая линия, включенная на выходе коммутационной схемы, объединяет выходы, принадлежащие к соседним шагам искания. Из приведенных схем это правило выполняется для схемы №…

№3

82. Основными характеристиками случайных потоков вызовов являются:

- интенсивность

- параметр

83. Одно из правил построения равномерных неполнодоступных схем формулируется следующим образом: каждая нагрузочная группа должна иметь одинаковое число общих линий с каждой другой нагрузочной группой. Для контроля за выполнением этого правила:

Строится матрица связности

84. Одной из характеристик неполнодоступного включения является матрица связности, число строк и столбцов которой равно:

Числу нагрузочных групп

85. Одной из характеристик неполнодоступного включения является матрица связности, в которой указывается число общих связей между выходами каждой пары нагрузочных групп. Чтобы неполнодоступная схема имела меньшую чувствительность к колебанию нагрузки по нагрузочным группам необходимо, чтобы:

- матрица связности была равномерной

- сумма по строкам и столбцам одинакова

86. Одно из правил построения равномерных неполнодоступных схем формулируется следующим образом: каждая линия, вкл-я в выходы коммутационной схемы, должна быть доступна одинаковому числу нагрузочных групп (или отличаться на единицу). Из приведенных схем это правильно выполняется для схемы №…

№2

87. Отношение общего числа выходов gD неполнодоступной схемы всех нагрузочных групп g с доступностью D к числу подключаемых линий V y=gD/V называют: