
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет переходных искажений при АМ.Содержание книги
Поиск на нашем сайте
Амплитудная модуляция. Амплитудный детектор выделяет огибающую входного сигнала, определяемого выражением (1.36). Представив амплитуду этого напряжения в виде выражения
разложим его по биному Ньютона
Учитывая, что
Следовательно, переходная помеха по соседнему каналу искажает постоянную составляющую на величину относительной ошибки:
и создает переменные составляющие на частотах
где Если крутизна спада характеристики ФНЧ достаточно большая и частота среза Пример 1.4. Определить относительную ошибку в системе с АМ поднесущих при Решение. Согласно выражению (1.40) ошибка по постоянной составляющей равна Ошибка по переменной составляющей при m = 1 равна
3.Расчет a для ЧМП, ПМП, ФМП. Для оценки помехоустойчивости дискретных (двоичных) элементарных сигналов используется вероятностный критерий. Наиболее высокой помехоустойчивостью обладает так называемый идеальный приёмник Котельникова, который обеспечивает при данном способе передачи наилучшую помехоустойчивость, называемую потенциальной. Потенциальная помехоустойчивость – это предельно допустимая помехоустойчивость, которая может быть обеспечена идеальным приёмником. Идея построения идеального приёмника заключается в том, что, зная, какие сигналы должны быть переданы, и имея их образцы, он сравнивает полученные сигналы
Если
Определим значение Передача двух дискретных сообщений видеоимпульсами с пассивной паузой, т.е.
где Как видно из (3.10),
Передача двух дискретных сообщений радиоимпульсами с прямоугольной огибающей и пассивной паузой (рис. 3.2, б). В этом случае Подставляя в (3.6) и производя интегрирование, получим, что при
Таким образом, заполнение видеоимпульса частотой не повышает его помехоустойчивость, а при той же амплитуде и длительности снижает её. Рассмотрим теперь потенциальную помехоустойчивость передачи двух дискретных сообщений с активной паузой. Активная пауза означает, что если сигнал Частотная манипуляция. Передача осуществляется радиоимпульсами на разнесённых частотах
При
При одинаковом динамическом диапазоне помехоустойчивость такой передачи эквивалентна помехоустойчивости при передаче видеоимпульсами с пассивной паузой (3.10). Полярная манипуляция. Передача осуществляется разнополярными прямоугольными импульсами длительностью t (рис. 3.2, г), т.е.
Из сравнения выражений (3.10) и (3.13) следует, что помехоустойчивость при передаче разнополярными импульсами в два раза выше, чем при передаче видеоимпульсами с пассивной паузой. Фазовая манипуляция. Передача осуществляется поочерёдно радиоимпульсами с одной и той же частотой, но с фазами, отличающимися на 180° (рис. 3.2, д), т.е.


Рис. 3.2. Передача двух дискретных сообщений: а – видеоимпульсами; б – радиоимпульсами; в – методом частотной манипуляции; Подставляя в (3.6) и учитывая, что
Сравнение выражений (3.10) и (3.14) показывает, что введение фазовой манипуляции приводит к улучшению помехоустойчивости. Если сравнить дискретные методы манипуляции, то окажется, что самой помехоустойчивой является фазовая манипуляция.
Описанная помехоустойчивость элементарных сигналов предполагает наличие идеального приёмника, для реализации которого требуется знание фазы несущей частоты и амплитуды сигнала, а также наличие синхронизации начала приёма сигнала.
Экзаменационный билет № 32
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.28.7 (0.008 с.) |

 ,
, и получим
и получим (1.39)
(1.39)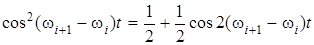 , и учитывая все члены не выше второй степени, получим
, и учитывая все члены не выше второй степени, получим .
. , (1.40)
, (1.40) и
и  составит величину
составит величину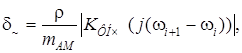 (1.41)
(1.41)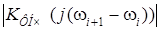 – коэффициент передачи выходного фильтра нижних
– коэффициент передачи выходного фильтра нижних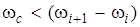 , то ошибками на частоте
, то ошибками на частоте  – коэффициент глубины АМ.
– коэффициент глубины АМ.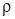 = 0,1,
= 0,1,  = 0,05 и
= 0,05 и  = 1.
= 1. .
.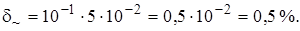
 по очереди с этими образцами [
по очереди с этими образцами [ 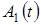 и
и  ] и, вычисляя энергию разности принятого сигнала и образца (величины
] и, вычисляя энергию разности принятого сигнала и образца (величины  или
или  ), относит принятый сигнал к тому сигналу, для которого эта разность минимальна.
), относит принятый сигнал к тому сигналу, для которого эта разность минимальна. , (3.2)
, (3.2) . (3.3)
. (3.3)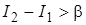 , то считаем принятым сигнал
, то считаем принятым сигнал  , а если
, а если 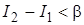 – сигнал
– сигнал  .
. – величина, характеризующая потенциальную помехоустойчивость,
– величина, характеризующая потенциальную помехоустойчивость, ; (3.6)
; (3.6)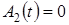
 , (3.10)
, (3.10) – удельная мощность помехи в полосе 1 Гц
– удельная мощность помехи в полосе 1 Гц  .
. , а
, а  .
.
 . (3.11)
. (3.11) и
и  (рис. 3.2, в). Помехоустойчивость характеризуется величиной
(рис. 3.2, в). Помехоустойчивость характеризуется величиной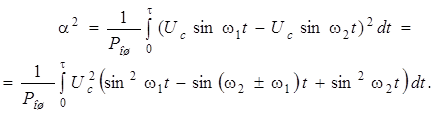
 ,
,  и
и  , что имеет место в реальных условиях, получим
, что имеет место в реальных условиях, получим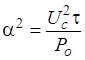 . (3.12)
. (3.12)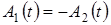 . Подставив значение в (3.6), получим
. Подставив значение в (3.6), получим . (3.13)
. (3.13) , а
, а  .
. , получим
, получим



