
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Помехоустойчивость двоичных неизбыточных кодов.Содержание книги
Поиск на нашем сайте
Кодовые комбинации состоят из условных единиц и нулей. При искажениях в кодовых комбинациях 1 может быть подавлена помехой и перейти в 0. Это означает, что сигнал 1 трансформировался в 0. Вероятность перехода 1® 0 обозначается как Таким образом, возможны два варианта передачи: – правильная передача – при этом 1 переходит в 1, т.е. – неправильная передача – при этом 1 переходит в 0, т.е. Вероятность правильной и неправильной передачи 1 и соответственно 0 определяется в соответствии с теоремой о полной группе событий
Если При проектировании эти вероятности задаются: – если состояние канала хорошее, то – если плохое, то При передаче двоичными неизбыточными кодами возможно два случая: – передача без ошибок, т.е. все сообщения переданы правильно и оцениваются вероятностью правильного приёма – передача с искажениями хотя бы одного элемента, которая оценивается вероятностью ошибки Вероятности
При расчётах – если в двоичном канале заданы вероятности двух переходов, то вероятности двух других переходов могут быть найдены на основе теоремы о полной группе событий (3.17) и (3.18); – вероятность того, что одна комбинация перейдёт в другую, равна произведению вероятностей переходов каждого символа. Например, передана комбинация 11001. Под воздействием помех эта комбинация исказится так, что будет вместо неё принята комбинация 10011. Определим, какова вероятность трансформации первой кодовой комбинации во вторую, если Для такой трансформации необходимо, чтобы во втором элементарном сигнале произошла ошибка типа 1 ® 0, а в четвёртом 0 ® 1. Все остальные элементы должны быть приняты верно. Согласно теореме умножения
Учитывая, что
Таким образом может быть определён любой член матрицы вероятностей трансформации.
где
a+b+c+d – число разрядов кодовой комбинации. Определим условную вероятность правильной передачи. Для правильной передачи кодовой комбинации необходимо, чтобы были правильно переданы все её элементы. Пусть комбинация состоит из
В частном случае для симметричного канала, когда
где
Вероятность любой ошибки при передачи i –й комбинации равна
Для симметричного канала
Если имеется
Для оценки помехоустойчивости необходимо знать вероятности передачи каждого сообщения
Вероятность возникновения ошибки при передаче i–го сообщения равна
Средняя вероятность ошибки за такт (время, в течение которого осуществляется передача всех сообщений) найдётся усреднением условных вероятностей ошибки по всем сообщениям с учётом вероятности их передачи
Пример 3.3. Найти вероятность возникновения двух или трёх ошибок при передаче кодовой комбинации Решение. При двух ошибках возможно Тогда вероятность возникновения двух ошибок Р (2)= Р (А®Б)+ Р (А®В)+ + Р (А®Г) + Р (А®Д) + Р (А®Е) + Р (А®Ж)= Р 11 Р 10 Р 10 Р 11 + Р 11 Р 11 Р 10 Р 10 + Р 10 ´ ´ Р 11 Р 11 Р 10+ Р 10 Р 10 Р 11 Р 11+ Р 11 Р 10 Р 11 Р 10 + Р 11 Р 10 Р 11 Р 10 Р 11 = 6 Р 11 Р 11 Р 10 Р 10 = = 6 Р 112 Р 102 = 6(1– Р 10)2 Р 102 » 6·10–6. При трёх ошибках возможно Тогда вероятность возникновения трёх ошибок P (З) = Р (А ® З) + Р (А ® И) + Таким образом, вероятность возникновения трёх ошибок существенно меньше вероятности возникновения двух ошибок. Пример 3.4. Определить вероятность правильного приёма и вероятность любой ошибки в простом двоичном коде с Решение. В соответствии с выражением (3.22) вероятность правильного приёма Экзаменационный билет № 31
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.14.208 (0.006 с.) |

 (вероятность трансформации 1 в 0). Вероятность ложного сигнала, т.е. перехода 0 в 1, возможна, если помеха возникает при отсутствии сигнала, т.е. когда посланный 0 трансформируется в 1 и обозначается
(вероятность трансформации 1 в 0). Вероятность ложного сигнала, т.е. перехода 0 в 1, возможна, если помеха возникает при отсутствии сигнала, т.е. когда посланный 0 трансформируется в 1 и обозначается  .
. , а 0 переходит в 0, т.е.
, а 0 переходит в 0, т.е.  или
или  и
и 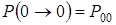 ;
; , или 0 переходит в 1, т.е.
, или 0 переходит в 1, т.е.  , или
, или  и
и  .
. , (3.17)
, (3.17) . (3.18)
. (3.18) , то образуется симметричный канал, т.е. в симметричном канале
, то образуется симметричный канал, т.е. в симметричном канале  и
и  равны между собой.
равны между собой. ,
, или определяются при испытаниях.
или определяются при испытаниях. ;
; .
. . (3.19)
. (3.19) известны.
известны. .
. и
и  , получим
, получим .
. , (3.20)
, (3.20) – число трансформации вида 0®1;
– число трансформации вида 0®1; – число трансформации вида 1®0;
– число трансформации вида 1®0; – число совпадающих единиц;
– число совпадающих единиц;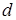 – число совпадающих нулей;
– число совпадающих нулей; нулей и m единиц. Тогда
нулей и m единиц. Тогда . (3.21)
. (3.21) ,
, при
при  , (3.22)
, (3.22) – число элементарных сигналов;
– число элементарных сигналов; – вероятность ошибочной передачи одного элементарного сигнала.
– вероятность ошибочной передачи одного элементарного сигнала. .
. . (3.23)
. (3.23) сообщений, то вероятность трансформации любого i- го сообщения в любое
сообщений, то вероятность трансформации любого i- го сообщения в любое  - е сообщение, где
- е сообщение, где  , определяется выражением
, определяется выражением . (3.24)
. (3.24) и все условные вероятности трансформации одних сообщений в другие
и все условные вероятности трансформации одних сообщений в другие  , задаваемые обычно в виде матрицы вероятностей трансформации.
, задаваемые обычно в виде матрицы вероятностей трансформации. . (3.25)
. (3.25) . (3.26)
. (3.26) . (3.27)
. (3.27) , если
, если  и
и  .
. типов искажений:
типов искажений:  типа искажений: З- 1000,
типа искажений: З- 1000,  .
. при передаче по симметричному каналу с
при передаче по симметричному каналу с  .
. .Вероятность возникновения любой из ошибок согласно (3.23)
.Вероятность возникновения любой из ошибок согласно (3.23) 



