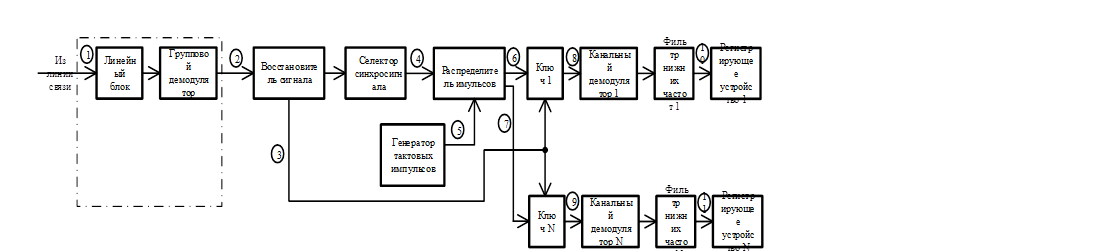
Структурная схема ПУ системы ти с врк.

На ПУ сигналы с выхода приемника поступают в восстановитель сигнала, где выделяется средняя часть видеосигнала, которая менее поражена помехами в канале связи. Восстановленный сигнал поступает на вход селектора синхросигнала и на вход всех канальных ключей. В селекторе синхросигнала происходит выделение синхронизирующих импульсов, из которых затем формируется сигнал для синхронизации приемного распределителя импульсов. Распределитель, формирующий N разнесенных по времени последовательностей импульсов, которые поступают на вторые входы канальных ключей и распределя ют измерительные импульсы по соответствующим информационным каналам. Сигналы каждого из каналов демодулируются в канальных демодуляторах, а затем через ФНЧ, который служит для увеличения отношения сигнал/шум, поступают в индивидуальные или многоканальные регистрирующие устройства.

В зависимости от видов первичной и вторичной модуляции различают следующие основные типы телеметрических систем с временным разделением каналов: АИМ-АМ, АИМ-ЧМ, ШИМ-АМ, ШИМ-ЧМ, ФИМ-АМ, ФИМ-ЧМ.

 

Расчет перекрестных искажений при аппроксимации АЧХ группового тракта полиномом.

Аппроксимация амплитудной характеристики группового тракта полиномом используется в тех случаях, когда предварительное ограничение группового тракта перед второй ступенью модуляции отсутствует, и аппроксимация линейно-ломаной становится грубым приближением. В этом случае амплитудную характеристику можно определить полиномом вида

,где , , – постоянные коэффициенты, величина и знак которых определяется видом характеристики.

Так как искажения группового тракта должны быть небольшими, то нелинейность реальной характеристики не будет значительной. Поэтому при анализе достаточно ограничения тремя первыми числами этого выражения.

Тогда ошибку от перекрестных помех можно представить в виде

.

В качестве примера предположим, что на вход поступают два сигнала и . Для простоты вычислений принимаем, что .

Тогда

. (1.27)

 

Из этого выражения видно, что в спектре даже при немодулированных поднесущих появляются комбинационные составляющие вида: ; ; ; ; . Причем число их резко возрастает с увеличением числа каналов. Так при числе каналов число комбинационных составляющих вида =20, а при число составляющих вида равно 90. Последнее обстоятельство является причиной ограничения числа каналов (до 18…20) в радиотелеметрических системах с частотным разделением каналов.

На основании выражения (1.27) можно установить, какие составляющие перекрестных помех попадают в полосу, занимаемую групповым сигналом, и определить мощность перекрестных помех: ,

где – мощность составляющих, попадающих в полосу группового тракта.

Расчеты показывают, что . (1.28) Принимая приближенно, что спектральная плотность перекрестной помехи в полосе группового сигнала равномерна, и пренебрегая влиянием квадратичного члена характеристики, получим выражение для спектральной плотности перекрестной помехи:

 

. (1.29)

Коэффициент можно найти из экспериментальной амплитудной характеристики группового тракта.

Среднеквадратичную ошибку от перекрестных искажений на выходе отдельного -го канала можно определить из выражений [1].

Для уменьшения влияния перекрестных искажений выбор поднесущих частот производят по коэффициентам (табл. 1.3), либо по таблицам стандартных частот (табл. 1.4).

Таблица 1.3

Типовые наборы коэффициентов

 

r 1	r 2	r 3	r 4	r 5	r 6
	1,3	1,8	2,45	3,0	4,5
	1,8	3,3	5,7	9,85	17,0
	2,3	3,95	9,0	18,7	35,0

3.Помехоустойчивость передачи непрерывных сообщений.

При рассмотрении потенциальной помехоустойчивости целесообразно разделить возможные виды модуляции на прямые и интегральные. Прямыми называются такие виды модуляции, при которых сигнал S (t) связан с передаваемым сообщением l(t) непосредственно. Если указанная связь осуществляется с помощью оператора, например интеграла, то такая модуляция называется интегральной. К прямым видам модуляции относятся АМ, ФМ, АИМ, ФИМ, ШИМ, а к интегральным – ЧМ и ЧИМ.

В теории потенциальной помехоустойчивости показано, что спектральная плотность шума на выходе идеального приемника при прямых видах модуляции определяется выражением

, (4.1)

где – среднее за время наблюдения Т значение

квадрата частной производной сигнала

S (l, t) по информационному параметру

l(t);

Р _{0 вх} – спектральная плотность шума на входе приемника.

Выражение (4.1) имеет следующее физическое толкование: чем сильнее изменяется сигнал S (t) под воздействием сообщения l(t), тем меньше погрешность идеального приемника.

При интегральных видах модуляции имеем

, (4.2)

где .

Из (4.1) и (4.2) следует, что Р _{0 вых} для прямых видов модуляции не зависит от частоты, а для интегральных возрастает прямо пропорционально квадрату частоты. Последнее объясняется тем, что при (Р_с / Р_ш)>>1 эффективное напряжение на выходе частотного детектора пропорционально девиации частоты, а его квадрат – квадрату частоты.

Чтобы определить дисперсию (мощность) шума на выходе приемника, необходимо учесть все шумовые составляющие в пределах выходной полосы . В соответствии с этим для непрерывных методов модуляции (АМ, ЧМ, ФМ) будем иметь

. (4.3)

Для импульсных видов модуляции (АИМ, ФИМ, ШИМ)

и . (4.4)

Поскольку в теории потенциальной помехоустойчивости приняты пределы изменения информационного параметра l(t) от –1 до +1, а мощность шума на выходе приемника равна дисперсии абсолютной ошибки и связана с приведенной среднеквадратичной ошибкой соотношением ,то

Таким образом, можно предложить следующий порядок получения выражений приведенной среднеквадратичной ошибки для различных видов модуляции:

– записывается выражение для соответствующего вида модуляции;

– находится частная производная для прямых видов модуляции и для интегральных видов модуляции;

– находится I среднее значение квадрата частной производной;

– по выражению (4.1) или (4.2) находится спектральная плотность шума на выходе приемника;

– определяется мощность шума на выходе приемника из выражения (4.3);

– находится приведенная среднеквадратичная ошибка по выражению (4.5).

Экзаменационный билет № 33