Лекция 10. Метод конечных элементов

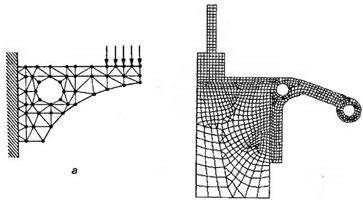
В современном проектировании широко используются различные программные пакеты автоматизированного конструирования, позволяющие оценивать проекты на каждом этапе процесса разработки. Средства CAE позволяют анализировать кинематику или динамику поведения проектируемого агрегата. В некоторых случаях сред­ства CAE позволяют определить распределение напряжений или температур в механических компонентах, рассчитанных на физическую или тепловую нагруз­ку. Возможно также проведение вибрационного анализа компонента, на который будет воздействовать динамическая нагрузка. Перечисленные задачи решаются при помощи средств анализа методом конечных элементов.

Универсальность этого метода удов­летворяет требованиям современных сложных систем конструирования, для ко­торых обычно отсутствуют замкнутые решения уравнений равновесия. Анализ методом конечных элементов начинается с аппроксимации исследуемой области (области задачи) и делении ее на ячейки сетки. На рисунке 8, апо углам каждой ячейки находятся узлы (черные точки). Такие ячейки и называются конеч­ными элементами.

Рисунок 8 – Аппроксимация объектов конечными элементами

 

В этом примере мы аппроксимировали исходный объект треугольниками и четырехугольниками, однако возможны и конечные элементы других типов. Вы­бор элементов определяется областью задачи, ее типом, а также конкретным па­кетом анализа. Выбор подходящих элементов с нужным количеством узлов из библиотеки доступных элементов является одним из наиболее важных решений, которые приходится принимать пользователю пакета конечно элементного ана­лиза. Конструктору также приходится задавать полное количество элементов (другими словами, их размер). Общее правило состоит в том, что чем больше ко­личество узлов и элементов (в р -версии) или чем выше степень функции формы (в р -версии), тем точнее оказывается решение, но тем дороже оно стоит с вычислительной точки зрения. Другая проблема –построение сетки, особенно для объек­та сложной геометрии. Создание трехмерных сеток конечных элементов обычно представляет собой трудоемкий и кропотливый процесс. Сейчас ведутся актив­ные разработки систем автоматизированного построения сеток, которые могли бы подключаться к системам геометрического моделирования. Такие системы позволили бы полностью интегрировать средства САМ и CAE.

После аппроксимации исходного объекта конечными элементами с должным ко­личеством узлов каждому узлу сопоставляется неизвестная величина, которая ищется в процессе решения задачи. Например, для рисунка 8, а неизвестными были бы смещения узлов по координатам х и у. Отсюда следует, что у каждого узла будет две степени свободы, а у задачи в целом будет 2п степеней свободы, если число узлов равно п. Функции формы служат лишь для того, чтобы вычислять значения неизвестных внутри элемента по заданным значениям на его узлах. После вычисления смещений программа может перейти к расчету деформаций как частных производных от функции смещения, а по деформациям рассчитываются напряжения.

Аппроксимировав область задачи набором дискретных конечных элементов, мы должны задать характеристики материала и граничные условия для каждого элемента. Указав различные характеристики для разных элементов, мы можем анализировать поведение объекта, состоящего из разных материалов. Граничные условия (смещение, внешняя сила или температура) обычно задаются на внеш­ней границе объекта. Эти условия должны быть выражены в виде значений сме­щения, силы или температуры в граничных узлах некоторых конечных эле­ментов. После задания граничных условий для всех внешних узлов программа конечноэлементного анализа формирует систему уравнений, связывающую гра­ничные условия с неизвестными (смещениями или температурой в узлах или коэффициентами функции формы в р -версии), после чего решает эту систему относительно неизвестных.

После нахождения значений неизвестных пользователь получает возможность рассчитать значение любого параметра в любой точке любого конечного элемен­та по той же функции формы, которая использовалась при построении системы уравнений. Выходные данные программы анализа методом конечных элементов обычно представляются в числовой форме. Однако по числовым данным пользователю бывает за­труднительно получить общее представление о поведении соответствующих па­раметров. Графические изображения обычно более информативны, поскольку дают возможность изучить поведение параметров на всей области задачи. Ана­лиз поведения параметров может производиться при помощи постпроцессора, который строит кривые и контурные графики переменных по данным програм­мы конечноэлементного анализа.

К преимуществам метода конечных элементов от­носится возможность работы с телами произвольной геометрии и неоднородны­ми материалами. Однако суть метода состоит в делении области задачи на набор конечных элементов и поиске наилучшего решения, непрерывного «внутри» эле­ментов, но имеющего возможность претерпевать скачки на их границах.

Моделирование конечных элементов.

Анализ методом конечных элементов является мощнейшей технологией, позво­ляющей моделировать распределение напряжений, температур, потоки жид­костей и распространение электромагнитных полей, однако до сих пор нерешен­ной остается проблема подготовки данных для проведения анализа: выбор геометрии, построение сетки конечных элементов, добавление граничных усло­вий и нагрузок, задание свойств материалов и выбор типа анализа (статический или динамический, линейный или нелинейный, анализ деформаций, напряже­ний и т. д.). Действия, относящиеся к подготовке данных, обобщенно называют моделированиемконечных элементов (finite-element modeling). Выполняются эти действия чаще всего препроцессором, рассчитанным на работу с какой-либо кон­кретной программой анализа методом конечных элементов (finite-element analysis – FEA).

Работа с препроцессором начинается с выбора геометрии объекта или области задачи. Традиционные системы FEA обладают лишь зачатками функций моде­лирования конечных элементов, тогда как большинство современных систем либо снабжаются расширенными средствами моделирования, либо позволяют обмениваться данными с системами геометрического моделирования (а иногда предлагают пользователю и то, и другое вместе). Системы, рассчитанные на подготовку геометрической модели в системах автоматизированной подготов­ки чертежей, либо работают непосредственно с данными CAD, либо преобразу­ют и импортируют их. Более того, использование CAD упрощает моделирование и дает возможность работать с более сложными функциями соз­дания и изменения геометрических форм. Современные гибридные системы мо­делирования (интегрирующие объемное, поверхностное и каркасное моделиро­вание с параметрическим и объектно-ориентированным подходами) позволяют создать практически любую нужную для анализа геометрию. Большинство сис­тем FEA могут также импортировать геометрические данные либо через проме­жуточные файлы стандартных форматов (типа IGES), либо непосредственно из конкретных CAD. Однако использование геометрических моделей, подготовлен­ных в CAD, не всегда оказывается простым делом. Модель, которую конструк­тор сочтет идеальной, может на самом деле содержать недопустимые в FEA эле­менты. Особенно это касается построения сеток. Некоторые системы уже предлагают функции проверки импортированных моделей. Более того, даже если построенная в CAD модель свободна от недостатков, она может быть черес­чур подробной. Например, такие характерные детали, как фаски, в некоторых случаях вполне могут быть исключены из модели для анализа методом конеч­ных элементов. Подобные решения принимаются конструктором исходя из ожи­даемого размера ячеек сетки, а также из интуитивных предположений о важно­сти отдельных участков объекта. Некоторые программы обладают функциями удаления элементов (defeaturing), то есть временного скрытия деталей, не влияющих на точность анализа. Абстрагирование является основной причиной различий между моделями одного и того же объекта, используемыми проекти­ровщиками и аналитиками. Изменения, предлагаемые одними из них, не могут непосредственно воплощаться в модели других. В настоящее время ведутся исследования возможности автоматического абстрагирования объемных моде­лей.

Следующий шаг – создание ячеек сетки и распределение узлов. Когда каждой ячейке сопоставляются узлы, она становится конечным элементом. Построение сетки является важнейшим и сложнейшим этапом моделирования. Для упроще­ния этой задачи практически все системы на сегодняшний день предлагают те или иные функции автоматизации. Наиболее типично использование тетраэдрических элементов для объемных тел и четырехугольных или треугольных эле­ментов для трехмерных поверхностей, оболочек и двухмерных объектов. Многие системы предоставляют пользователям возможность изменять параметры авто­матически формируемых сеток, в частности плотность ячеек. Кроме того, в та­ких системах обычно имеются функции ручного локального редактирования, по­зволяющие уточнить сетку в критических областях. Многие системы связывают сетку с геометрической моделью, так что изменение последней автоматически влечет за собой изменение первой.

От сложности сетки зависит размер глобальной матрицы жесткости, численная сложность задачи и объем требуемых вычислительных ресурсов. Точность реше­ния можно повысить увеличением количества ячеек или использованием функ­ций формы более высоких порядков. Конечные элементы должны удовлетворять определенным требованиям. Во-первых, размерность элементов должна совпа­дать с размерностью области задачи. Для одномерных задач используются одно­мерные элементы, для двумерных — двумерные, и т. д. Во-вторых, конечные эле­менты должны поддерживаться выбранной программой FEA. Другими словами, программа должна уметь рассчитывать вклад конкретного элемента в матрицу жесткости. Все элементы, поддерживаемые пакетом анализа, составляют его биб­лиотеку (element library). Чем больше элементов в библиотеке, тем большее число задач может решать программа.

За выбором элементов следует задание типа анализа (статический или динами­ческий, линейный или нелинейный, анализ деформаций, напряжений и т. д., как уже отмечалось). С каждым узлом связываются неизвестные или степени свобо­ды. К неизвестным относятся смещения, повороты, температура, тепловые пото­ки и т. п. Затем задаются граничные условия. Для непрерывных границ объекта известными могут быть смещения, внешние силы и температура. Эти сведения должны быть выражены в виде значений соответствующих параметров в кон­кретных граничных узлах. Иногда требуется формирование конечных элементов без граничных условий. Если необходимо учесть точечные воздействия, в соот­ветствующих точках должны располагаться узлы. Большинство систем анализа, интегрированных с CAD, дают пользователю возможность задавать граничные условия непосредственно на геометрической, модели, после чего эти гранич­ные условия преобразуются к эквивалентным условиям на узлах системы. На­грузки и граничные условия задаются множеством способов, что позволяет решать задачи самого широкого круга и моделировать реальные условия доста­точно точно. Для каждого элемента обязательно задание свойств материала. Обычно эти па­раметры включают модуль Юнга и коэффициент Пуассона (для задач строи­тельной механики). Толщина оболочек и пластин рассматривается скорее как свойство материала, чем как геометрический параметр, что позволяет избежать перехода к трем измерениям. Для задач других типов могут быть заданы тепло­емкость или вязкость. Разные элементы могут иметь разные свойства, благодаря чему пользователь может анализировать составной объект, о чем уже говорилось выше. Основные сложности в описании составных объектов возникают при за­дании интерфейсов.

Полностью определенная конечноэлементная модель со всеми параметрами пе­редается программе анализа. Решенная задача подготавливается к исследованию постпроцессором. Большинство пакетов позволяют вычислять различные пара­метры, выводить их в виде таблиц или графиков. Чаще всего требуется вывод данных о деформациях, напряжениях и изменении формы. Для этой цели тради­ционно используются контурные графики, на которых распределение парамет­ров кодируется различными цветами непосредственно на изображении объекта. Большинство пакетов уже ушли довольно далеко от столь примитивной графи­ки. Пользователь современной системы может выводить на экран изоповерхности (поверхности с постоянными значениями какого-либо параметра) или попе­речные сечения. Для динамического анализа удобно наличие средств анимации, позволяющих проводить нелинейный анализ временной эволюции систем. Все более возрастает потребность в выводе графиков и роликов в форматах, пригод­ных для использования в других программах, документах, презентациях и Сети.

Автоматическое построение сетки. Построение сетки подразумевает определение положения узлов и элементов, а также автоматическую нумерацию узлов и элементов с минимальным объемом вводимых пользователем данных. Предполагается, что методы полностью авто­матического формирования сетки (fully automatic mesh generation) требуют толь­ко задания геометрической модели (геометрии и топологии) объекта, подлежа­щего разбиению на элементы, свойств сетки, таких как плотность ячеек и типы элементов, а также граничных условий, включающих внешние нагрузки. Мето­ды, не входящие в эту категорию, могут требовать ввода дополнительных дан­ных, в частности разбиения объекта на несколько частей. Такие методы считаются полуавтоматическими.

Соединение узлов. Чрезвычайно популярный подход к проблеме построения сетки состоит в соеди­нении узлов. Популярность этого подхода объясняется простотой его концеп­ции. Метод делится на две основные фазы: создание узлови по­строение элементов.

Литература 2 осн. [225-257], 2 доп. [115-129]

Контрольные вопросы

1. Чем заключается универсальность метода конечных элементов?

2. С чего начинается анализ методом конечных элементов?

3. Как называются действия, относящиеся к подготовке данных?

4. Что подразумевается под автоматическим построением сетки?

5. Какова последовательность САЕ методом конечных элементов?