Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні розрахункові залежностіСодержание книги
Поиск на нашем сайте
Наступним етапом у проектуванні активних фільтрів повинен бути вибір електричних ланок, які б мали необхідні передавальні функції. При цьому, як правило, передавальні функції фільтрів представляються у виді добутку дробово-раціональних множників, які мають у чисельнику і знаменнику поліноми, не вищі за другий порядок. Згідно з цим, для реалізації фільтрів необхідні типові ланки 1-го і 2-го порядків. Ланка першого порядку – це просте пасивне RC – коло. Схема ланки 2-го порядку залежить від виду дробово-раціональної передавальної функції [10, 12]. В табл. 6.1 наведені коефіцієнти передавальних функцій для фільтрів різних типів. Величини в табл.1: q1 – рівень мінімумів пульсації АЧХ у смузі пропускання (рівень максимумів прийнято за 0 дБ); q2 – рівень максимумів пульсації в смузі затухання. Передавальна функція ланки ФНЧ 1-го порядку має вигляд:
Передавальна функція ланки ФВЧ 1-го порядку має вигляд:
Схеми ланок ФНЧ і ФВЧ 1-го порядку наведено на рисунку 6.11.
Для того, щоб показані на рис. 6.11 ланки мали вищенаведені передавальні функції необхідно виконати умови:
для ФНЧ: для ФВЧ: де К0, К∞ - коефіцієнти підсилення по напрузі, fз – частота зрізу за рівнем – 3 дБ. У фільтрах 3-го порядку заданий коефіцієнт передачі у смузі пропускання К0 або К∞ реалізується звичайною ланкою 2-го порядку, тому ланку 1-го порядку у таких фільтрах можна спростити, прийнявши, що К0 та К∞ = 1. При цьому замість операційних підсилювачів DA1 можна використати звичайні емітерні та витокові повторювачі.
а
б
а – ланка ФНЧ, б – ланка ФВЧ
Рисунок 6.11 – Схеми ланок ФНЧ і ФВЧ 1 – го порядку В наслідок того, що передавальні функції фільтрів 2-го і вищих порядків характеризуються наявністю комплексно-спряжених полюсів, реалізувати їх за допомогою звичайних RC – кіл не можливо. Для реалізації ланок із заданими передавальними функціями існує велика кількість схем, наприклад: пасивні ланки на основі RLC - контура, гіратори, конвертори негативного опору, операційні ланки з багатоступеневим ЗЗ і т.ін. Найбільш розповсюдженою ланкою 2-го порядку є фільтр Саллена – Кея. Схеми ланок ФНЧ і ФВЧ 2-го порядку наведені на рис. 6.12. Передавальна функція для ФНЧ знаходиться з виразу:
Якщо задати К0 = 1, то DA1 можна замінити повторювачем напруги, а подільник R3, R4 виключити зі схеми. При цьому передавальна функція (6.15) набуде вигляду:
Оскільки ряд номінальних значень ємностей конденсаторів вужчий за аналогічний ряд резисторів, то при розрахунку доцільно ємностями С1 і С2 задаватися. При цьому К0 = 1, а опори резисторів R1, R2 визначається з виразу:
а
б а – ланка ФВЧ, б – ланка ФНЧ
Рисунок 6.12 – Схеми ланок ФНЧ і ФВЧ 2 – го порядку
Для того, щоб значення R1, R2 були дійсними повинна виконуватись умова: C2/C1 ≥ 4bi / ai2. Рівнокомпонентний фільтр можна отримати за умови, що R1 = R2 = R та С1 = С2 = С. У цьому випадку для реалізації доданих компонентів передавальної функції bі і аі слід змінювати значення К0. Передавальна функція рівнокомпонентного фільтра НЧ 2-го порядку має вид:
Елементи схеми розраховуються з умов:
Передавальна функція ФВЧ 2-го порядку має вигляд:
Прийнявши К∞ = 1 і С1 =С2 =С, отримаємо:
При цьому елементи схеми фільтра розраховуються за формулами:
У рівнокомпонентній ланці ФВЧ R1=R2=R, С1=С2=С, а передавальна функція має вид:
Елементи схеми фільтра розраховуються з виразу:
Конкретні значення R і С для всіх ланок слід вибирати таким чином, щоб одночасно задовольнялись рівності:
де Rвх і Rвих – вхідні та вихідні опори DA1. Невиконання цих умов може призвести до значного відхилення реальної добротності та частоти зрізу ланки від розрахункових, що проявиться у спотворенні АЧХ усього фільтра.
Таблиця 6.1 - Розрахункові коефіцієнти для активних фільтрів
Для формування фільтрів 3 і 4 порядків необхідно послідовно з´єднати ланки 1-го і 2-го, або 2-го і 1-го порядків. Порядок розташування ланок у фільтрах 3 і 4 порядків не впливає на результуючу АЧХ цього фільтра.
Контрольні запитання до теми «АКТИВНІ ФІЛЬТРИ»
1. Що таке активні фільтри і чим вони відрізняються від пасивних? 2. Якого типу ланки фикористовуються у активних фітрах? 3. Для чого наводяться коефіцієнти передавальних функцій? 4. Якого типу сигнали використовуються у техніці та яка між ними різниця? 5. Навести основні характеристики аналогових та цифрових сигналів. 6. Що таке фільтрація сигналу та його спектр? 7. Навести класифікацію фільтрів. 8. Якого виду бувають АЧХ та ФЧХ фільтрів? 9. Що таке передавальна функція фільтра? 10. Яка різниця між аналоговими та цифровими фільтрами? 11. Які властивості має фільтр типу «цегляна стінка»? 12. Як здійснити технічну реалізацію активного фільтра на операційних підсилювачах? 13. Як впливає порядок фільтра на його характеристики? 14. Що таке синтез фільтра і у чому він полягає? 15. чи залежать характеристики фільтра від розміщення фільтруючих ланок у ньому? 16. Навести галузі використання пасивних та активних фільтрів. 17. Що дає застосування у фільтрі операційного підсилювача? 18. Чи можна активні фільтри застосувати для фільтрації напруги живлення ЗВТ? 19. Чи змінює активний фільтр спектр вихідного сигналу? 20. Чи можна з’єднувати фільтри паралельно, або послідовно? Л Е К Ц І Я № 12
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.70.169 (0.006 с.) |

 (6.13)
(6.13) (6.14)
(6.14)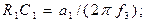
 ;
;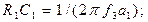
 ;
;

 (6.15)
(6.15)
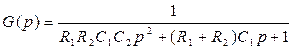 (6.16)
(6.16) (6.17)
(6.17)

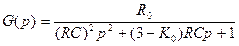 (6.18)
(6.18)
 ; (6.19)
; (6.19) (6.20)
(6.20) (6.21)
(6.21)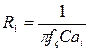
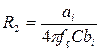 (6.21)
(6.21) (6.22)
(6.22)
 (6.23)
(6.23) та Rвих<<R<< Rвх
та Rвих<<R<< Rвх