
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По виду начальной и рабочей информации.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обыкновенные САУ – системы, требующие для построения функционирования наибольшей начальной информации. Самонастраивающиеся САУ – системы, не требующие для построения функционирования полной начальной информации об управляемом процессе. Принцип деления систем - используемая информация. Рабочая информация передаётся в виде сигналов.
Задачи самонастраивающимся адаптивным САУ: · Поддержание режима близкого к оптимальному – наилучшему · Поддержание оптимальной работы системы по условию максимального быстродействия.
Игровые системы - системы, в которых принцип действия основывается на формирование команд управления на основе составления множества решений, выборов на каждом этапе управляемой операции. Критерием сопоставления различных возможных решений – выборов служит некоторый показатель – функция выгоды.
Математическая модель системы управления — это пара "оператор системы и модель внешних воздействий". Оператором системы называется закон, в соответствии с которым система преобразует внешнее (входное) воздействие g в выходной сигнал х (рис. В.4). Оператор системы. Функция, которая любому значению аргумента x ставит в соответствие некоторый элемент y множества Y, не являющегося множеством чисел, называется оператором. Под понятием оператора объединяются любые математические действия: все алгебраические действия, дифференцирование, интегрирование, сдвиг во времени, решение дифференциальных, интегральных, алгебраических и любых других функциональных уравнений, а также любые логические действия. Задать оператор системы – это значит задать совокупность (программу) действий, которые надо осуществить над входной функцией, чтобы получить выходную функцию.
Рис. В.4
По виду оператора системы управления делятся на: а) линейные и нелинейные; б) непрерывные, дискретные, непрерывно-дискретные; в) нестационарные и стационарные; г) детерминированные и стохастические; д) одномерные и многомерные; е) с сосредоточенными и с распределенными параметрами. Внешние воздействия делятся на: а) непрерывные (функции непрерывного аргумента) и дискретные (функции дискретного аргумента);
б) детерминированные и случайные; в) одномерные и многомерные. Чтобы классифицировать конкретную систему, нужно указать на шесть классов, к которым принадлежит оператор системы, и на три класса, к которым принадлежат внешние воздействия. Например, она может оказаться линейной непрерывно-дискретной нестационарной детерминированной одномерной с сосредоточенными параметрами при непрерывных случайных одномерных внешних воздействиях. Поясним названия классов операторов на примере описания систем дифференциальными или разностными уравнениями. Линейные системы описываются линейными дифференциальными уравнениями, нелинейные — нелинейными дифференциальными уравнениями. Непрерывные системы описываются дифференциальными уравнениями; дискретные — разностными; непрерывно-дискретные — дифференциально-разностными уравнениями. Нестационарные системы описываются уравнениями с переменными коэффициентами, стационарные — уравнениями с постоянными коэффициентами. Детерминированные системы описываются уравнениями, коэффициенты которых являются детерминированными величинами или функциями времени, стохастические — стохастическими уравнениями. Одномерные системы имеют один вход и один выход, многомерные системы имеют суммарное число входов и выходов, большее двух. Наконец, системы с сосредоточенными параметрами описываются обыкновенными дифференциальными уравнениями, с распределенными параметрами — уравнениями в частных производных.
Несмотря на существенное разнообразие технических процессов, построение аппаратуры управления и автоматических систем основывается на ряде общих принципов управления, основные из которых следующие: принцип управления по отклонению, принцип управления по возмущению, принцип комбинированного управления и принцип адаптации. Принцип автоматического управления определяет, как и на основе какой информации формировать управляющее воздействие в системе. Одним из основных признаков, характеризующих принцип управления, является требуемая для выработки управляющего воздействия рабочая информация, а следовательно, и конфигурация цепей передачи воздействий в системе. Выбор принципа построения автоматической системы зависит от ее назначения, характера изменения задающего и возмущающих воздействий, возможностей получения необходимой рабочей информации, стабильности параметров управляемого объекта и элементов управляющего устройства и т. п.
Принцип управления по отклонению. Если в автоматической системе управляющее воздействие вырабатывается на основе информации об отклонении управляемой величины от требуемого значения, то говорят, что система построена на основе принципа управления по отклонению, или принципа обратной связи. Для реализации этого принципа в управляющем устройстве необходимо осуществлять сравнение действительного значения управляемой величины с требуемым (предписанным) значением и управлять объектом в зависимости от результатов этого сравнения.
Принцип управления по отклонению является универсальным и эффективным, поскольку он позволяет управлять неустойчивыми объектами, а также осуществлять требуемый закон изменения управляемой величины с допустимо малым отклонением (ошибкой) независимо от того, какими причинами последнее вызвано. Так, например, влияние возмущающего воздействия f (t) в системе (рис. 3) можно значительно ослабить без непосредственного его измерения благодаря свойствам обратной связи.
Принцип управления по возмущению. Принцип управления по возмущению, или принцип компенсации возмущений, состоит в том, что управляющее воздействие в системе вырабатывается в зависимости от результатов измерения возмущения, действующего на объект. Системы, построенные по этому принципу, работают по разомкнутой цепи, т. е. не имеют обратной связи. Системы с разомкнутой цепью воздействий разделяют на две группы: системы компенсации и системы программного управления. В настоящее время принцип управления по возмущению широко применяется, потому что он позволяет уменьшить погрешности автоматических систем, вызываемые как задающими, так и возмущающими воздействиями. Его основное достоинство — высокое быстродействие цепей компенсации, так как система реагирует непосредственно на причину, а не на следствие. Однако этот принцип имеет недостатки. Основной из них — избирательность: не всегда возможно измерить и учесть все возмущения. Обычно учитывается действие лишь одного или нескольких наиболее существенных возмущений, которые измеряются управляющим устройством.
Принцип комбинированного управления. Современные автоматические системы высокой точности обычно строят на основе принципа комбинированного управления, сочетающего в себе принципы управления по отклонению и по возмущению. При этом в автоматических системах комбинированного управления наряду с замкнутыми контурами, образуемыми отрицательными обратными связями, имеются цепи компенсации основного возмущающего воздействия hк или дополнительная цепь компенсации ошибок от задающего воздействия хвх. Принцип адаптации. Рассмотренные принципы автоматического управления долгое время были единственными. Однако успешное развитие кибернетики позволило применить в автоматических системах новый принцип управления, называемый принципом адаптации (приспособления). Отличительные особенности этого принципа поясним на примере самонастраивающейся автоматической системы, которая состоит из основной системы и дополнительных устройств.
Известны следующие формы математического описания непрерывных систем: дифференциальными уравнениями, переходными функциями, интегральными и спектральными преобразованиями, а также две формы описания дискретных систем: разностными уравнениями и Z-преобразованием.
Линеаризация уравнений движения.
Работу любой автоматической системы в установившемся и переходном режиме можно описать, использовав дифференциальные уравнения, которые применимы для описания многих явлений природы и, в частности, процессов преобразования и передачи массы или энергии
У реальных элементов и систем связь между входными и выходными величинами, как правило, нелинейная, общее уравнение системы оказывается нелинейным, а аналитическое решение нелинейных уравнений возможно только в редких частных случаях. Поэтому полученные нелинейные уравнения элементов системы необходимо линеаризовать. Линеаризация уравнений — это замена точного нелинейного уравнения приближенным линейным. Например, алгебраическое нелинейное уравнение
можно заменить приближенным линейным уравнением
Отметим, что уравнение (17) записано в отклонениях, а не в абсолютных значениях переменных величин. Основным допущением, на котором базируется линеаризация, является предположение, что независимая переменная изменяется в небольших пределах. Оценим аналитически, какими же должны быть эти пределы. Функцию у в уравнении типа (16) можно разложить в ряд Маклорена в окрестностях точки
где Д0 = у — у0. Уравнение (19) является приближенным по отношению к уравнению (18), так как мы пренебрегли слагаемыми высших порядков малости. При этом чем меньше отклонение переменных от их установившихся значений, тем меньше ошибка при замене нелинейного уравнения линейным.
Действительно, из рис. 55 и уравнения (19) следует, что линеаризация уравнения (16) соответствует замене точной кривой у = х2 прямой, касательной в точке линеаризации А, В тех случаях, когда функция зависит от нескольких переменных, в качестве коэффициентов линейного уравнения будут стоять не простые, а частные производные.
МОДЕЛИ ТИПА «ВХОД-ВЫХОД» Математические модели (1.1), (1.2) описывают взаимосвязи между переменными состояния системы, поэтому их называют внутренними. Модели, отражающие зависимость между входными и выходными сигналами системы, называют внешними. Пусть рассматривается линейная система с одним входом и одним выходом, процессы в которой описываются неоднородным линейным дифференциальным уравнением л-го порядка
где u(t), u(q)(t) — входной сигнал системы и q = 1, т его производных; y(t), ym(t) — выходной сигнал системы и к = 1, п его производных. Применив к этому уравнению оператор дифференцирования Коши D = d/d/, получим операторное представление уравнения системы:
Запишем это представление в иной форме у = B(D)/A(D)u, где обозначено
Выражение H(D) — B(D)/A(D) называют операторной передаточной функцией системы, а уравнение y(t) = H(D)u(t) (1.8) операторной или внешней моделью системы. Полином A(D) называют характеристическим многочленом системы, его корни — полюсами или характеристическими числами системы, а корни полинома B(D) — нулями системы. Представление внешней модели в частотной области позволяет осуществить преобразование Лапласа. Пусть лапласовы преобразования входного и выходного сигналов:
, тогда моделью системы оказывается выражение Y(s) = H{s)U{s), (1.9) полученное преобразованием уравнения (1 .7) при нулевых начальных условиях. Выражение H(s) называют передаточной функцией системы.
В теории автоматического управления широко применяется операторная (символическая) форма записи дифференциальных уравнений. В операторной форме дифференциальные уравнения приобретают более простой вид, уменьшается объем записи, а при исследовании САУ во многих случаях сокращаются промежуточные математические преобразования.
Функции независимой переменной (обычно t)- x (t), y (t) в дифференциальных уравнениях заменяются их изображениями по Лапласу.
В изображениях по Лапласу операция дифференцирования обозначается следующим образом:
а интегрирования – обратной величиной:
Метод преобразования Лапласа применяется для упрощения решения систем линейных интегро-дифференциальных уравнений с постоянными коэффициентами. Прямое преобразование заданной системы уравнений приводит к более простым уравнениям, которые являются уже не интегро-дифференциальными, а алгебраическими уравнениями. Эта более простая система уравнений решается относительно изображения искомой функции, по которому затем отыскивается искомое решение заданной системы уравнений с помощью обратного преобразования Лапласа. Оба преобразования, прямое и обратное, на практике выполняются с помощью соответствующих таблиц.
то при нулевых начальных условиях это уравнение в операторной форме запишется так:
Передаточной функцией (в форме преобразований Лапласа) называется отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях. При P=0 передаточная функция превращается в коэффициент усиления.
k=
Динамической характеристикой системы называют ее реакцию на специальное входное возмущение. Такими специальными — типовыми — сигналами являются: • импульсная дельта-функция {функция Дирака)
• единичный скачок (функция Хевисайда)
линейное воздействие
гармоническое воздействие
■5800
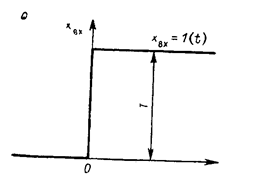
Для оценки динамических свойств звеньев используют временные и частотные характеристики, К временным характеристикам звеньев относятся их переходные функции. Переходная функция звена h(t) определяет его реакцию на единичную ступенчатую функцию x вх=1(t) (рис. 2.1, а) и характеризует переход звена от одного установившегося состояния к другому (рис. 2.1,6). Выражение функции h(t) можно получить посредством решения дифференциального уравнения, которым описывается динамика данного звена при хъх=1(t) и нулевых начальных условиях. За единичную ступенчатую функцию принимают скачкообразное воздействие с величиной скачка, равной единице при t>0:
Ступенчатый сигнал — весьма распространенный вид входного воздействия в САУ, например мгновенный поворот задающей оси следящего привода, мгновенное изменение момента нагрузки электропривода и т. д.-
Другим также распространенным видом входного воздействия в САУ является единичная импульсная входная функция или дельта-функция, представляющая собой производную единичной ступенчатой функции:
Дельта-функции свойственна тождественность нулю повсюду, кроме точки t=0, в которой она стремится к бесконечности {рис. 2.2, а), т. е.
Площадь дельта-функции равна единице, т. е.
и наоборот
Учитывая это простое соотношение между переходной и весовой функциями, в дальнейшем будем использовать в основном первую из них, имея в виду, что вторую всегда можно получить из выражения (2.5). Через скачок или импульс можно выразить непрерывные сигналы любой формы, представив их в виде суммы скачков или импульсов определённой интенсивности, подаваемых в определённые моменты времени или через равные промежутки времени. Найдя реакцию системы на каждый скачок (импульс) и просуммировав результат, получим реакцию системы на суммарный входной сигнал.
Пусть сигнал представлен некоторой функцией времени х (t). Используя интеграл Дюамеля в различной форме, данный сигнал можно представить совокупностью единичных скачков
при а -> 0 или совокупностью единичных импульсов
Если входной сигнал задан функцией времени x (t). то сигнал на выходе звена может быть получен с помощью переходной или весовой функции. Разлагая х (0 на совокупность единичных скачков 1Р'(t — т) по формуле (ЗЛ) и находя реакцию звена на каждый из скачков, определяем
Аналогично, разлагая x (t} на совокупность единичных импульсов б (t — т) по формуле (3,2) и находя реакцию звена на каждый из импульсов, получаем
Таким образом, рассмотренные характеристики звеньев дают возможность рассчитать сигнал на выходе звена, если известен сигнал на его входе при нулевых начальных условиях* Рассмотрим частотную функцию, которая является важнейшей характеристикой динамического звена.
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.130.174 (0.014 с.) |



 Таким образом, работу контура самонастройки можно представить как процесс автоматической настройки управляющего устройства основной системы по совокупности текущей информации об изменяющихся условиях работы для достижения поставленной цели управления.
Таким образом, работу контура самонастройки можно представить как процесс автоматической настройки управляющего устройства основной системы по совокупности текущей информации об изменяющихся условиях работы для достижения поставленной цели управления.




 Так как величина
Так как величина  малая, то все слагаемые в формуле (18), кроме первого и второго, будут иметь высшие порядки малости, и ими можно пренебречь. Поскольку величина
малая, то все слагаемые в формуле (18), кроме первого и второго, будут иметь высшие порядки малости, и ими можно пренебречь. Поскольку величина  постоянная, то в результате получим линейное уравнение
постоянная, то в результате получим линейное уравнение 


















 (1 .7)
(1 .7)

















 =
= 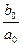









 . Примером импульсного воздействия может быть кратковременный ток короткого замыкания генератора, который отключается плавкими предохранителями, кратковременный удар нагрузки на валу электродвигателя и т.д.
. Примером импульсного воздействия может быть кратковременный ток короткого замыкания генератора, который отключается плавкими предохранителями, кратковременный удар нагрузки на валу электродвигателя и т.д.










