
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формальное определение грамматики и языка.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте ВВЕДЕНИЕ.
Языки программирования или, как их часто называют, алгоритмические языки, являясь средством общения человека с электронными вычислительными машинами, начали развиваться одновременно с появлением последних, т.е. примерно пять десятилетий назад. С момента своего появления языки программирования, а также методы их описания, изучения и использования интенсивно развивалось, и в настоящее время составляют обширную и важную область прикладной математики. Являясь новой областью математики, теория формальных языков, к которым относятся и языки программирования, еще не вполне оформилась как математическая дисциплина. В противоположность многим разделам классической математики методы изучения формальных языков разработаны недостаточно, а используемые в этих методах классы объектов не всегда удовлетворительно отражают свойства языков. В настоящем пособии освещаются наиболее существенные синтаксические особенности алгоритмических языков и используемые в настоящее время методы их описания и изучения.
ГРАММАТИКИ И ЯЗЫКИ. ОБСУЖДЕНИЕ ГРАММАТИК.
Рассмотрим предложение " The big elephant ate the peanut". Если мы знаем английский, то поймем, что это предложение английского языка. Его можно изобразить в виде схемы, которая представлена на рисунке 1.1.
Рис.1.1. Синтаксическое дерево. Схема предложения, такая, например, как на рис.1.1, называется синтаксическим деревом. Оно описывает синтаксис, или структуру, предложения, разлогая его на составные части. Таким образом, мы видим, что <предложение> состоит из <подлежащее>, за которым следует <сказуемое>; <подлежащее> состоит из <артикль>, за которым следует < прилагательное >, за которым в свою очередь следует <существительное> и т.д. Для того чтобы описать структуру, мы использовали новые символы - "синтаксические единицы" или "синтаксические классы", такие, как <предложение>. Эти символы заключаются в угловые скобки "<" и ">", чтобы отличить их от слов самого языка. Мы узнаем, что " The big elephant ate the peanut" является предложением, либо, основываясь на интуиции, либо применяя соответствующие правила грамматики, выученные в школе; конечно, каждый из нас мог бы составить неформальное синтаксическое дерево для любого простого английского предложения. Однако для того, чтобы иметь возможность механически разбирать предложения, мы должны дать точные формальные правила, которые описывают структуру предложений. Для этой цели мы создадим метаязык, т.е. некий язык, на котором можно описывать другие языки. В английских школах в курсе французского языка английский язык используется при описании французского языка. Следовательно, английский играет роль метаязыка. В учебниках английского языка английский язык используется для описания самого себя. В настоящий момент нас в основном интересует описание синтаксиса (структуры) языков программирования, а не их семантики (смысла); схемы, такие, как на рис. 1.1., не передают смысла предложения. Такое синтаксическое описание мы называем грамматикой языка. Метаязык, который мы будем использовать, впервые был предложен Хомским для описания естественных языков. Конкретная система записи, которой мы воспользуемся, принадлежит Бэкусу. По мнению Хомского, этот метаязык полезен лишь для описания небольших подмножеств, состоящих из простых предложений, и не совсем удовлетворителен даже для описания структуры простых формальных языков, таких как Фортран и Паскаль. Однако, мы воспользуемся им, поскольку в нем наилучшим образом сочетается мощность и целесообразность практического использования. Еще раз рассмотрим предложение "The big elephant ate the peanut". Как мы отмечали, рис.1.1 показывает, что < предложение > состоит из < подлежащее >, за которым следует <сказуемое>. Если сократить фразу "может состоять из", заменив ее символом::=, то наша грамматика могла бы содержать, например, такие правила:
Заметим, что грамматика может содержать более одного правила, в котором описывается образование конкретной синтаксической единицы. Например, на рис. 1.1 есть два правила, которые показывают, из чего может состоять <существительное>. Если имеется множество правил, то ими можно воспользоваться для того, чтобы вывести, или породить, предложение по следующей схеме. (По этой причине такие правила часто называют правилами вывода, или продукциями.) Начнем с синтаксической единицы <предложение>, найдем правило, в котором <предложение> слева от::=, и подставим вместо <предложение> цепочку, которая расположена справа от::=, т.е. <предложение> => < подлежащее > <сказуемое> Таким образом, мы заменяем синтаксическую единицу на одну из цепочек, из которых она может состоять. Повторим процесс. Возьмем одну из синтаксических единиц в цепочке < подлежащее > <сказуемое>, например < подлежащее >; найдем правило, где < подлежащее > находится слева от::=, и заменим < подлежащее > в исходной цепочке на соответствующую цепочку, которая находится справа от::=. Это дает
<подлежащее> <сказуемое> => <артикль> <прилагательное > <существительное> <сказуемое> Символ "=>" означает, что один символ слева от => в соответствии с правилом грамматики заменяется цепочкой, находящейся справа от =>. Полный вывод предложения будет таким:
Этот вывод предложения запишем сокращенно, используя новый символ "=>+": <предложение> =>+ the big elephant ate the peanut На каждом шаге можно заменить любую синтаксическую единицу. В приведенном выше выводе мы всегда заменяли самую левую из них. Обратите также внимание на то, что такое правило, как <предложение>::= <подлежащее><сказуемое>, можно использовать для описания многих различных предложений; для этого необходимо только иметь различные способы образования синтаксических единиц <подлежащее> и <сказуемое>. Из семи правил
мы можем образовать целых девять предложений!
Одно из назначений грамматики как раз и состоит в том, чтобы описать все предложения языка с помощью приемлемого числа правил. Это важно, если учесть тот факт, что обычно количество предложений в языке бесконечно. После такого введения мы почти готовы описать формальные понятия грамматик и языков, но далее нам все-таки придется прежде определить некоторые термины, которыми мы пока пользовались неформально.
СИМВОЛЫ И ЦЕПОЧКИ. Мы неформально определяем язык как подмножество множества всех предложений из "слов" или символов некоторого основного словаря. И опять - таки нас не интересует смысл этих предложений. Например, английский язык состоит из предложений, которые являются последовательностями, составленными из слов (if, he, is и т.д.), и знаков пунктуации (запятые, точки, скобки). Язык программирования ПАСКАЛЬ состоит из программ, которые являются последовательностями, составленными из таких символов, как if, begin, end, знаков пунктуации, букв и цифр. Язык четных целых чисел состоит из последовательностей, составленных из цифр 0,1,...9, в которых последней цифрой должны быть 0,2,4,6 или 8. О п р е д е л е н и е 1.1. АЛФАВИТ - это непустое конечное множество элементов. Назовем элементы алфавита символами. Всякая конечная последовательность символов алфавита А называется цепочкой. Вот несколько цепочек "в алфавите" А={a,b,c}:a,b,c,ab,aaca. Мы также допускаем существование пустой цепочки l, т.е. цепочки, не содержащей ни одного символа. Важен порядок символов в цепочке; так, цепочка ab не то же самое, что ba, и abca отличается от aabc. Длина цепочки х (записывается как |х|) равна числу символов в цепочке. Таким образом, |l|=0, |а|=1. |abb|=3. Заглавные буквы M,N,S,T,U,... используются как переменные или имена символов алфавита, в то время как строчные буквы t,u,v,w... используются для обозначения цепочек символов. Таким образом, можно написать х=STV, и это означает, что х является цепочкой, состоящей из символов S,T и V именно в таком порядке. Если х и у-цепочки, то их конкатенацией ху является, полученная путем дописывания символов цепочки у вслед за символами цепочки х. Например, если х=XY, у=YZ, то ху=XYYZ и ух=YZXY. Поскольку l - цепочка, не содержащая символов, в соответствии с правилом катенации для любой цепочки х мы можем написать lх=хl=х. Если z=ху - цепочка, то х - голова, а у - хвост цепочки z. И, наконец, х- правильная голова, если у - не пустая цепочка. Таким образом, если х=abc, то l,a,ab и abc суть головы х, и к тому же все они, кроме abc, - правильные головы. Множества цепочек в алфавите обычно обозначаются заглавными буквами А,В,.... Произведение АВ двух множеств в цепочке А и В определяется как АВ={ху|хÎА, а уÎВ} и читается как "множество цепочек ху, такое, что х из А, а у из В". Например, если А={a,b} и B={c,d}, то множество AB={ac,ad,bc,bd}. Поскольку lх=хl=х справедливо для любой цепочки х, мы имеем {l}A=A{l}=A. Заметьте, что здесь символ заключен в фигурные скобки. Произведение определено для множеств, тогда как l является символом, а не множеством. {l}-это множество, состоящее из пустого символа l. Мы можем теперь определить степени цепочек. Если x1=x, x2=xx, x3=xxx
Для n>0 имеем xn=xxn-1=(xn-1)x. Так же можно определить степени алфавита А: A0={l}, A1=A, An=AAn-1 для n>0. Используя это, определим две последние операции в этом разделе - итерацию А* множества А и усеченную итерацию А+ множества А: А+=А1 È А2 È... È Аn È..., А*=А0 È А+. Таким образом, если А={a,b}, то А* включает цепочки l,a,b,aa,ab,bb,aaa,aab.... Заметим, что А+=АА* =(А*)А. П р и м е р 1.1.: Пусть z=abb. Тогда |z|=3. Головы z есть l,a,ab,abb. Правильные головы z есть l,a,ab. Хвосты z - это l,b,bb,abb. Правильные хвосты z - это l,b,bb. Пусть х=а, z=abb.Тогда zx=abba, xz=aabb, z0=l, z1=abb, z2=abbabb, z3=abbabbabb, |z0|=0, |z1|=3, |z2|=6,|z3|=9. Пусть S={a,b,c}. Тогда S+={a,b,c,aa,ab,bb,bc,ca,cb,cc,aaa,...}. S*={l,a,b,c,aa,ab,ac,...}. Иногда удобнее и, как правило, нагляднее писать х... вместо ху, если нас не интересует у - остальная часть цепочки. Таким образом, три точки "..." обозначают любую возможную цепочку, включая и пустую. Наиболее часто встречаются следующие обозначения: Обозначение Смысл z=х... х - голова цепочки z. Нам безразличен хвост. z=...х х - хвост цепочки z. Нам безразлична голова. z=...х... х встречается где-то в цепочке z. z=S... Символ S - первый символ цепочки z. z=...S Символ S - последний символ цепочки z. z=...S... Символ S встречается где-то в цепочке z.
ЗАДАЧА РАЗБОРА.
Разбор сентенциальной формы означает построение вывода и, возможно, синтаксического дерева для нее. Программу разбора называют также распознавателем, так как она распознает только предложения рассматриваемой грамматики. Именно это и является нашей задачей в данный момент, поскольку мы хотим распознавать программы, написанные на языке программирования. Все алгоритмы разбора, которые мы описываем, называются алгоритмами разбора слева направо ввиду того, что они обрабатывают сначала самые левые символы рассматриваемой цепочки и продвигаются по цепочке вправо только тогда, когда это необходимо. Мы могли бы подобным же образом определить разбор справа налево, но он менее естествен. Инструкции в программе выполняются слева направо, да и мы читаем тоже слева направо. Различают две категории алгоритмов разбора: нисходящий (сверху вниз) и восходящий (снизу вверх). Эти термины соответствуют способу построения синтаксических деревьев. При нисходящем разборе дерево строится от корня (начального символа) вниз к концевым узлам. Рассмотрим предложение 35 в следующей грамматике целых чисел (последовательностей, состоящих из одной и более цифр): (1.7) N::=D | N D D::=0|1|2|3|4|5|6|7|8|9 На первом шаге непосредственный вывод N=>N D будет строиться так, как это показано в первом дереве на рис.1.8. На каждом последующем шаге самый левый нетерминал V текущей сентенциальной формы хVу заменяется на правую часть u правила V::=u, в результате чего получается следующая сентенциальная форма. Этот процесс для предложения 35 представлен на рис.1.8 в виде пяти деревьев. Фокус в том, конечно, что надо получить ту сентенциальную форму, которая совпадает с заданной цепочкой. Метод восходящего разбора состоит в том, что, отправляясь от заданной цепочки, пытаются привести ее к начальному символу. На первом шаге при разборе предложения 35 терминал 3 приводится к D, в результате чего получается сентенциальная форма D5. Таким образом, мы построили непосредственный вывод D5=> 35, как это показано в самом правом частичном синтаксическом дереве на рис.1.9. На следующем шаге D приводится к N, что показано во втором дереве справа. Этот процесс продолжается до тех пор, пока не будет получено первое дерево рис.1.9. Мы расположили деревья на рисунке справа налево, потому что такое расположение лучше иллюстрирует построенный вывод, который теперь читаем, как обычно, слева направо. Заметим, что выводы, произведенные двумя различными распознавателями, различны, но имеют одно и то же синтаксическое дерево. Поскольку мы будем часто ссылаться на тип вывода, который получается при восходящем разборе слева направо, введем еще один новый термин. Заметим, что в таком разборе на каждом шаге редуцируется основа (самая левая простая фраза) текущей сентенциальной формы и поэтому цепочка справа от основы всегда содержит только терминальные символы.
Рис.1.8. Нисходящий разбор и построение вывода.
Рис.1.9. Восходящий разбор и построение вывода.
О п р е д е л е н и е 1.11. Непосредственный вывод хUу => х u у называется каноническим и записывается хUу => х u у, если у содержит только терминалы. Вывод w=>+v называется каноническим и записывается w=>+v, если каждый непосредственный вывод в нем является каноническим. Каждое предложение, но не каждая сентенциальная форма имеет канонический вывод. Рассмотрим в качестве примера сентенциальную форму 3D грамматики 1.7. Ее единственным выводом является <число>=>ND=>DD=>3D И второй, и третий непосредственные выводы не являются каноническими, но это не должно нас смущать, поскольку мы в основном интересуемся разбором (анализ) программ, которые являются предложениями языка программирования. Сентенциальная форма, которая имеет канонический вывод, называется канонической сентенциальной формой. Мы, конечно, еще не касались главных проблем разбора. 1. Предположим, что при нисходящем разборе надо заменить самый левый нетерминал V, и пусть имеется n правил: V::=x1|х2|...|хn. Как узнать, какой цепочкой хi следует заменить V? 2. При восходящем разборе на каждом шаге редуцируется основа. Как найти основу и то, к чему она должна приводиться? На эти вопросы не всегда легко ответить. Одним из решений является выбор некоторого из возможных вариантов наугад в предположении, что он верен. Если позднее обнаружится ошибка, то мы должны вернуться назад и попытаться применить другой вариант. Этот прием называется возвратом. Очевидно, что возвраты могут привести к чрезмерному расходу времени. Другим решением является просмотр контекста вокруг обрабатываемой в данный момент подцепочки. Именно так мы поступаем, когда вычисляем выражение, подобное А+В*С. Мы задаем себе вопрос, "можно ли вначале вычислить А+В", и отвечаем на него отрицательно, замечая, что за А+В следует *. Один из первых алгоритмов разбора, который действительно использовался в компиляторе, был описан Айронсом. Метод, положенный в основу этого алгоритма, являлся смесью нисходящего и восходящего методов, и мы не будем обсуждать его подробнее.
ДИАГРАММЫ СОСТОЯНИЙ.
Рассмотрим регулярную грамматику G[Z]: Z::=U0|V1 U::=Z1|1 V::=Z0|0 Легко видеть, что порождаемый ею язык состоит из последовательностей, образуемых парами 01 или 10, т.е. L(G)= {Bn|n>0}, где B={01,10}. Чтобы облегчить распознавание предложений грамматики G, нарисуем диаграмму состояний (рис. 2.1). В этой диаграмме каждый нетерминал грамматики G представлен узлом или состоянием; кроме того, есть начальное состояние S (предполагается, что грамматика не содержит нетерминала S). Каждому правилу Q::=T в G соответствует дуга с пометкой T, направленная от начального состояния S к состоянию Q. Каждому правилу Q::=RT соответствует дуга с пометкой T, направленная от состояния R к состоянию Q. Мы используем диаграммы состояний, чтобы распознать или разобрать цепочку x следующим образом: 1. Первым текущим состоянием считать начальное состояние S. Начать с самой левой литеры в цепочке x и повторять шаг 2 до тех пор, пока не будет достигнут правый конец x. 2. Сканировать следующую литеру x, продвинуться по дуге, помеченной этой литерой, переходя к следующему текущему состоянию. Если при каком-то повторении шага 2 такой дуги не оказывается, то цепочка x не является предложением и происходит останов. Если мы достигаем конца x, то x - предложение тогда и только тогда, когда последнее текущее состояние есть Z. В этих действиях можно узнать восходящий разбор. На каждом шаге (кроме первого) основой является имя текущего состояния, за которым следует входной символ. Символ, к которому приводится основа, будет именем следующего состояния. В качестве примера проведем разбор предложения 101001. Каждая строка на рис.2.2,a отражает состояние разбора перед началом выполнения шага 2.
Рис.2.1. Диаграмма состояний.
Рис.2.2. Разбор и синтаксическое дерево для цепочки 101001. a - разбор; б - синтаксическое дерево.
В этом примере разбор выглядит столь простым благодаря простому характеру правил. Так как нетереминалы встречаются лишь как первые символы правой части, на первом шаге первый символ предложения всегда приводится к нетерминалу. На каждом последующем шаге первые два символа UT сентенциальной формы UTt приводятся к нетерминалу V, при этом используется правило V::=UT. При выполнении этой редукции имя текущего состояния - U, а имя следующего текущего состояния - V. Так как каждая правая часть единственна, то единственным оказывается и символ, к которому она приводится. Синтаксические деревья для предложений регулярных грамматик всегда имеют вид, подобный изображенному на рис.2.2,б. Чтобы избавиться от проверки на каждом шаге, есть ли дуга с соответствующей пометкой, можно добавить еще одно состояние, называемое F (НЕУДАЧА), и добавить все необходимые дуги от всех состояний к F. Добавляется также дуга, помеченная всеми возможными литерами и ведущая из F обратно в F. В результате диаграмма, показанная на рис.2.1,а изменится и станет такой, как на рис.2.1,б.
ПОСТРОЕНИЕ КА ИЗ НКА.
Итак, при работе НКА возникает проблема, которая заключается в следующем: мы не знаем, какую выбрать дугу на каждом шаге, если существует несколько дуг с одинаковой пометкой. Теперь покажем, как из НКА построить КА, который как бы параллельно проверяет все возможные пути разбора и отбрасывает тупиковые. То есть если в НКА имеется, к примеру, выбор из трех состояний X, Y, Z, то в КА будет одно состояние [XYZ], которое представляет все три. Напомним, что возможные состояния на каждом шаге работы НКА - это подмножество полного множества состояний и что число различных подмножеств конечно. Т е о р е м а 2.1. Пусть НКА=(K, VT, M, S, Z) допускает множество цепочек L. Определим КА F'=(K', VT,M',S',Z') следующим образом: 1. Алфавит состояний K' состоит из всех подмножеств множества K. Обозначим элемент множества K' через [S1,S2,...,Si], где S1,S2,..., Si - состояние из K. (Допустим впредь, что состояния S1,S2,...,Si расположены в некотором каноническом порядке таким образом, что, например, состояние из K' для подмножества {S1, S2}={S2, S1} - суть [S1, S2].) 2. Множество входных литер VT для F и F' одно и тоже. 3. Отображение M' определим как M'([S1,S2,...,Si], T)=[R1,R2,..., Rj], где M({S1,S2,...,Si}, T)={R1,R2,... Rj}. 4. Пусть S={S1,...,Sn}. Тогда S'=[S1,..., Sn]. 5. Пусть Z={Sj,Sk,..., Sl}. Тогда Z'=[Sj,Sk,...,Sl]. Утверждается, что F и F' допускают одно и то же множество цепочек.
Рис.2.4. Диаграммы состояний.
П р и м е р 2.2. На рисунке (2.4) приведена диаграмма состояний НКА с начальным состоянием S и P и одним заключительным состоянием Z. Справа показана диаграмма состояний соответствующего КА, у которого начальное состояние [S,P], а множество заключительных состояний {[Z],[S,Z],[P,Z], [S, P,Z]}. Заметим, что состояния [S] и [P,Z] можно исключить, так как нет путей, ведущих к ним. Таким образом, построенный КА не является минимальным - возможен автомат с меньшим числом состояний. Отображение М (рис.2.4.а) Отображение M’(рис.2.4.б) M(S,0)=P M’(S,0)=P M(S,1)={S,Z} M’(S,1)=[S,Z] M(P,0)=Æ M’(SP,0)=[P, Æ]=P M(P,1)=Z M’(SP,1)=[S,Z] M(Z,0)=P M’(P,0)= M(Z,1)=P M’(P,1)=Z M’(PZ,0)=P M’(PZ,1)=PZ M’(SZ,0)=P M’(SZ,1)=[SPZ] M’(SPZ,0)=P M’(SPZ,1)=[SPZ] M’(Z,0)=P M’(Z,1)=P
НИСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ. MOV – основная команда общего назначения, позволяющая пересылать байт или слово между регистром и ячейкой памяти или между двумя регистрами. Она может также пересылать непосредственно адресуемое значение в регистр или в ячейку памяти. ADD – складывает содержимое операнда – источника и операнда – приемника и помещает результат в операнд – приемник. SUB – вычитает операнд – источник из операнда – приемника и помещает результат в операнд – приемник. MUL – умножает числа без знака и заносит результат по умолчанию в регистр – аккумулятор, используемый для выполнения арифметических операций над данными. DIV – выполняет деление чисел без знака, где источник – делитель, находящийся в регистре общего назначения или в ячейке памяти, а делимое по умолчанию извлекается из регистра – аккумулятора. Слова AH, AL, AX, BH, BL, BX, BP, CH, CL, CS, DH, DL, DX, DI, DS, ES, SI, SP, ST являются зарегистрированными именами регистров (аккумуляторы). Представленные в таблице 5 мнемокоды, будем использовать далее в конкретных примерах. Например, фрагмент программы, реализующий расчет выражения W=X+Y+24-Z может выглядеть следующим образом: Директивы определения данных, команды ввода и др. X,Y,W,Z определены как переменные-слова. MOV AX, X;передать (X) в AX ADD AX, Y;прибавить (Y) к AX ADD AX, 24;прибавить 24 к сумме SUB AX,Z;вычесть (Z) из (X)+(Y)+24 MOV W, AX;запомнить результат в W
5.2. ОСНОВНЫЕ ЧАСТИ КОМПИЛЯТОРА. Перевод (трансляция) — это некоторое отношение между цепочками, или, другими словами, это некоторое множество пар цепочек. Компилятор определяет перевод, образуемый парами вида (исходная программа, объектная программа). Существуют два фундаментальных метода организации перевода. Первый из них предполагает перевод программы написанной на языке высокого уровня в программу на машинном языке или на языке ассемблера (объектную программу), что предполагает разработку компилятора. Второй пооператорно считывает исходную программу, переводит их в машинные коды и сразу выполняет, минуя объектную программу, что предполагает разработку интерпретатора. Желательные качества транслятора таковы: 1) эффективность трансляции - время необходимое для обработки входной цепочки (программы) линейно зависит от ее длины; 2) небольшой объем; 3) корректность – желательно иметь небольшой конечный тест, такой, что если транслятор прошел через него, то правильность работы транслятора гарантированна для всех входных программ. Во многих компиляторах для многих языков программирования есть общие процессы. Попытаемся выделить сущность некоторых из этих процессов. При этом мы постараемся устранить из них по возможности все, что связано с конкретной реализацией и зависит от машины и операционной системы. Хотя соображения, относящиеся к реализации, важны (плохая реализация может испортить хороший алгоритм), нам кажется, что понимание фундаментальной природы проблемы существенно само по себе и позволяет применить технику, созданную для решения этой проблемы, к другим проблемам, по существу сходным с нею. Исходная программа, написанная на некотором языке программирования, есть не что иное, как цепочка знаков. Компилятор в конечном итоге превращает эту цепочку знаков в цепочку битов — объектный код. В этом процессе часто можно выделить подпроцессы со следующими названиями: (1) Лексический анализ. (2) Работа с таблицами. (3) Синтаксический анализ, или разбор. (4) Генерация кода, или трансляция в промежуточный код (например, язык ассемблера). (5) Оптимизация кода. (6) Генерация объектного кода (например, ассемблирование). В конкретных компиляторах порядок этих процессов может несколько отличаться от указанного, а некоторые из них могут объединяться в одну фазу. Кроме того, никакая входная цепочка не должна нарушать работу компилятора, т.е. он должен обладать способностью, реагировать на любую из них. Для входных цепочек, не являющихся синтаксически правильными программами, компилятор должен выдать соответствующие сообщения об ошибках. Мы кратко опишем первые пять фаз компиляции. В реальном компиляторе они не обязательно разделены. Однако методически часто оказывается удобным расчленить компилятор на эти фазы, чтобы изолировать проблемы, присущие именно этим частям процесса компиляции.
ЛЕКСИЧЕСКИЙ АНАЛИЗ.
Первая фаза — лексический анализ. Входом компилятора, а следовательно, и лексического анализатора, служит цепочка символов некоторого алфавита. Алфавит Pascal А В С... Z 0... 9 _ пробел + - / * = < > [ ].,;: () ’ Основные символы языка (терминалы) подразделяются на буквы цифры и специальные символы – знаки, имеющие фиксированный смысл. Зарезервированное cлово = and array begin case const div downto do else end file for function goto if in label mod nil not of or packed procedure program record repeat set then to type until var while with. В программе некоторые комбинации символов часто рассматриваются как единые объекты. Среди типичных примеров можно указать следующие: 1) В таких языках, как Pascal, цепочка, состоящая из одного или более пробелов, обычно рассматривается как один пробел. 2) В языках есть ключевые слова, такие, как Begin, End, integer, и составные знаки:=, <=,>= и т.д. каждое из которых считается одним символом (зарезервированные слова). 3) Каждая цепочка, представляющая числовую константу, рассматривается как один элемент текста. 4) Идентификаторы, используемые как имена переменных, функций, процедур, меток и т. п., также считаются лексическими единицами языка программирования. Работа лексического анализатора состоит в том, чтобы сгруппировать определенные терминальные символы в единые синтаксические объекты, называемые лексемами. Какие объекты считать лексемами, зависит от определения языка программирования. Лексема - это цепочка терминальных символов, с которой мы связываем лексическую структуру, состоящую из пары вида (тип лексемы, некоторые данные). Первой компонентой пары является синтаксическая категория, такая как «константа» или «идентификатор», а вторая - указатель: в ней указывается адрес ячейки, хранящей информацию об этой конкретной лексеме. Для данного языка число типов лексем предполагается конечным. Пару (тип лексемы, указатель) тоже будем называть лексемой, когда это не будет вызывать недоразумений. Таким образом, лексический анализатор - это транслятор, входом которого служит цепочка символов, представляющая исходную программу, а выходом - последовательность лексем. Этот выход образует вход синтаксического анализатора. П р и м е р 5.1. Рассмотрим следующий оператор присваивания из языка, подобного Pascal: COST:= (PRICE + TAX) * 30 На этапе лексического анализа будет обнаружено, что COST, PRICE и TAX - лексемы типа идентификатора, а 30 - лексема типа константы. Знаки:= (+) * сами являются лексемами. Допустим, что все константы и идентификаторы нужно отобразить в лексемы типа <ид>. Мы предполагаем, что вторая компонента лексемы представляет собой указатель элемента таблицы, содержащего фактическое имя идентификатора вместе с другими, собранными нами данными об этом конкретном идентификаторе. Первая компонента используется синтаксическим анализатором для разбора. Вторая компонента используется на этапе генерации кода для изготовления подходящего машинного кода. Таким образом, выходом лексического анализатора, работающего на нашей входной цепочке, будет последовательность лексем <ид>1:= (<ид>2 + <ид>3) * <ид>4 Здесь вторая компонента лексемы (указатель данных) показана в виде нижнего индекса. Символы:=, +, * трактуются как лексемы, тип которых представлен ими самими. Они не имеют связанных с ними данных и, значит, не имеют указателей. Лексический анализ провести легко, если лексемы, состоящие более чем из одного знака, изолированы с помощью знаков, которые сами являются лексемами. В примере знаки:=, +,* не могут быть частью идентификатора, так что COST, PRICE и TAX легко выделяются как лексемы. Мы определим два крайних подхода к лексическому анализу. Большинство известных способов основано на том или другом из этих подходов, а некоторые на их комбинации. (1) Говорят, что лексический анализатор работает прямо, если для данного входного текста (цепочки) и положения указателя в этом тексте анализатор определяет лексему, расположенную непосредственно справа от указываемого места, и сдвигает указатель вправо от части текста, образующей эту лексему. (2) Говорят, что лексический анализатор работает не прямо, если для данного текста, положения указателя в этом тексте и типа лексемы он определяет, образуют ли знаки, расположенные непосредственно справа от указателя, лексему этого типа. Если да, то указатель передвигается вправо от части текста, образующей эту лексему. Вообще мы будем описывать алгоритмы синтаксического анализа в предположении, что лексический анализ прямой. В случае непрямого лексического анализа можно использовать “недетерминированные” алгоритмы или алгоритмы с возвратами. После того как в результате лексического анализа лексемы распознаны, информация о некоторых из них собирается и запасается в одной или нескольких таблицах. Какова эта информация, зависит от языка. В случае Pascal, например, мы хотели бы знать, что COST, PRICE и TAX – переменные с плавающей точкой, а 30 – целая константа. В сложных языках, таких, как Pascal, объем сведений, которые надо запомнить о данной переменной, может быть очень велик. Рассмотрим несколько упрощенный пример таблицы, в которой хранится информация об идентификаторах. Такую таблицу часто называют таблицей имен (а также таблицей идентификаторов и таблицей символов). В ней перечислены, в частности, все идентификаторы вместе с относящейся к ним информацией. Допустим, что в тексте встречается оператор COST:= (PRICE + TAX) * 30 После просмотра этого оператора таблица может иметь вид таблицы 5.2. Если позднее во входной цепочке попадется идентификатор, надо справиться в этой таблице, не появлялся ли он раньше. Если да, то лексема, соответствующая новому вхождению этого идентификатора, будет той же, что и у предыдущего вхождения. Например, если в программе, написанной на Pascal, после указанного выше оператора следует оператор, содержащий переменную COST, то лексемой для второго вхождения COST должна быть <ид>1 - та же, что и для первого вхождения.
Таблица 5.2
Таким образом, эта таблица должна обеспечивать (1) быстрое добавление новых идентификаторов и новых сведений о них, (2) быстрый поиск информации, относящейся к данному идентификатору. Обычно применяют метод хранения данных с помощью таблиц расстановки.
СИНТАКСИЧЕСКИЙ АНАЛИЗ. Как уже упоминалось, выходом лексического анализатора является цепочка лексем. Эта цепочка образует вход синтаксического анализатора, исследующего только первые компоненты лексем - их типы. Информация о каждой лексеме (вторая компонента) используется на более позднем этапе процесса компиляции для генерации машинного кода. Синтаксический анализ, или разбор, как его еще называют, - это процесс, в котором исследуется цепочка лексем и устанавливается, удовлетворяет ли она структурным условиям, явно сформулированным в определении синтаксиса языка. Какова синтаксическая структура данной цепочки, существенно знать также и при генерации кода. Например, синтаксическая структура выражения А+В*С должна отражать тот факт, что сначала перемножаются В и С, а потом результат складывается с А. При любом другом порядке операций нужное вычисление не получится. Разбор - одна из наиболее понятных фаз компиляции. По совокупности синтаксических правил можно автоматически построить синтаксический анализатор, который будет проверять, имеет ли исходная программа синтаксическую структуру, определяемую этими правилами. Изложим несколько различных методов разбора и алгоритмов построения синтаксических анализаторов по заданной грамматике. Выходом анализатора служит дерево, которое представляет синтаксическую структуру, присущую исходной программе. В некотором отношении синтаксический анализ программы напоминает разбор предложений, который все мы проводили в школе. П р и м е р 5.2. Допустим, что выход лексического анализатора — цепочка лексем: <ид>1:= (ид>2 + <ид>3)*<ид>4 Эта цепочка передает информацию о том, что необходимо выполнить в точности следующее: (1) <ид>3 прибавить к <ид>2, (2) результат (1) умножить на <ид>4, (3) результат (2) поместить в ячейку, зарезервированную для <ид>1 Эту последовательность шагов можно представить наглядно с помощью помеченного дерева, показанного на рис.5.1 Внутренние вершины дерева представляют те действия, которые надо выполнить. Прямые потомки каждой вершины либо представляют аргументы, к которым нужно применить действие (если соответствующая вершина помечена идентификатором или является внутренней), либо помогают определить, каким должно быть это действие (в частности, это делают знаки +, *,:=)• Заметим, что скобки в цепочке в дереве явно не указаны, хотя мы могли бы изобразить их в качестве прямых потомков вершины n1. Роль скобок только в том, что они влияют на порядок операций. Если бы в рассматриваемой цепочке их не было, следовало бы поступить согласно обычному соглашению о том, что умножение “предшествует” сложению, и на первом шаге перемножить <ид>3 и <ид>4.
Рис. 5.1 Древовидная структура. ГЕНЕРАЦИЯ КОДА.
Дерево, построенное синтаксическим анализатором, используется для того, чтобы получить перевод входной программы. Этот перевод может б
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.018 с.) |




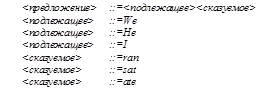

 , и в общем случае xn определяется как х - цепочка, то х0 - пустая цепочка l,
, и в общем случае xn определяется как х - цепочка, то х0 - пустая цепочка l,









