Детерминированный конечный автомат.

 

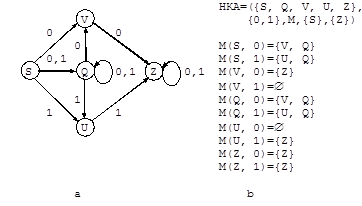
Чтобы иметь возможность легко манипулировать с диаграммами состояний, нам необходима дальнейшая формализация концепции терминах состояний, входных литер, начального состояния S, "отображения" М, которое по заданному текущему состоянию Q и входной литере T указывает следующее текущее состояние, и заключительных состояний, аналогичных состоянию Z в приведенном выше примере.

О п р е д е л е н и е 2.1. (Детерминированный) автомат с конечным числом состояний (КА) - это пятерка (K, VT, M, S, Z), где

1) K - алфавит элементов, называемых состояниями;

2) VT - алфавит, называемый входным алфавитом (литеры, которые могут встретиться в цепочке или предложении);

3) M - отображение (или функция) множества K x VT во множество K (если M(Q,T)=R, то это означает, что из состояния Q при входной литере T происходит переключение в состояние R);

4) S(ÎK) - начальное состояние;

5) Z - непустое множество заключительных состояний, каждое из которых принадлежит K.

Мы можем также формально определить, как работает КА (или диаграммы состояний) с входной цепочкой t. Сделаем это, расширив понятие отображения, которое указывает нам, как переключаются состояния в зависимости от входной литеры. Определим:

М(Q, l)=Q при любых Q;

M(Q,Tt)=M(M(Q,T),t) для любых tÎVT^* и TÎVT.

Первая строка означает, что если на входе пустой символ, то состояние остается прежним. Вторая строка показывает, что в состоянии Q и при входной цепочке Tt мы применяем M, чтобы перейти в состояние P=M(Q,T) с входной цепочкой t, и затем применяем цепочку t (цепочка t считается допускаемой), если M(S,t)=P, где состояние P принадлежит множеству заключительных состояний Z.

Такие автоматы называются детерминированными, так как на каждом шаге входная литера однозначно определяет следующее текущее состояние.

П р и м е р 2.1. Диаграмме состояний, показанной на рис.2.1, соответствует KA ({S, Z, U, V, F}, {0, 1}, M, S, {Z}), где

 

Теперь остановимся на некоторое время и посмотрим, чего же мы достигли. Мы начали с рассмотрения регулярной грамматики, которая имела единственные правые части. Для нее мы смогли построить диаграмму состояний. Эта диаграмма фактически была неформальным представлением KA. Легко видеть, что если предложение x принадлежит грамматике G, то оно также допускается KA, соответствующим грамматике G. Несколько труднее показать, что для любого KA существует грамматика G, порождающая только те предложения, которые являются цепочками, допускаемыми KA.

 

Представление в ЭВМ.

 

KA с состояниями S₁,...,S_n и входными литерами T₁,...,T_m можно представить матрицей В, состоящей из n x m элементов. Элемент В[i,j] содержит число k - номер состояния S_k, такого, что M[S_i,T_j]=S_k. Можно условиться, что состояние S₁ - начальное, а список заключительных состояний представлен вектором. Такая матрица иногда называется матрицей переходов, поскольку она указывает, каким образом происходит переключение из одного состояния в другое.

Другим способом представления может быть списочная структура. Представление каждого состояния с k дугами, исходящими из него, занимает 2*k+2 слов. Первое слово - имя состояния, второе - значение k. Каждая последующая пара слов содержит терминальный символ из входного алфавита и указатель на начало представления состояния, в которое надо перейти по этому символу.

 

2.3. НЕДЕТЕРМИНИРОВАННЫЙ КА.

 

Мы попадаем в затруднительное положение при построении KA, если G содержит правила

V::=UT и W::=UT

с одинаковыми правыми частями. Это означает, что в диаграмме состояний есть две дуги, помеченные T и исходящие из U, и отображение M оказывается неоднозначным! Автомат, построенный по такой диаграмме, называется недетерминированным KA и определяется следующим образом:

О п р е д е л е н и е 2.2. Недетерминированным KA или НКА называется пятерка (K, VT, M, S, Z) где

1) K - алфавит состояний;

2) VT - входной алфавит;

3) M - отображение множества K x VT в подмножества множества K;

4) SÎK - множество начальных состояний;

5) ZÎK - множество заключительных состояний.

И опять важным отличием является то, что отображение M дает не единственное состояние, а (возможно, пустое) множество состояний.

Второе отличие состоит в том, что может быть несколько начальных состояний. Как и ранее, расширим отображение М до K x VT^*, определяя

M(Q, l)={Q} и

M(Q, Tt) - как объединение множеств M(P, t), где PM(Q,T) для каждого TVT и tVT⁺. Продолжим расширение, определяя M({P₁,P₂,...,P_n}, t) как объединение множеств M (P_i, t) для i=1,..., n.

Цепочка t допускается автоматом, если найдется состояние P, которое принадлежит одновременно M(S, t) и множеству заключительных состояний Z.

В качестве примера рассмотрим регулярную грамматику G[Z]:

Z::= U1| V0 | Z0 | Z1

U::= Q1 | 1

V::= Q0 | 0

Q::= Q0 | Q1 | 0 | 1

Краткое рассмотрение показывает, что язык L(G) представляет собой множество последовательностей из 0 и 1, содержащих, по крайней мере, два смежных 0 или две смежные 1. (Чтобы убедиться в этом, начните вывод предложений из Z). На рис.2.3,а приводится соответствующая диаграмма состояний, а на рис.2.3,б - НКА. Состояние НЕУДАЧА представлено здесь подмножеством , не содержащим символов.

Проблема состоит в том, что теперь на каждом шаге может быть более одной дуги, помеченной следующей входной литерой, так что мы не знаем, какой путь выбрать. На каждом шаге известна основа текущей сентенциальной формы, но не известно, к чему она приводится. Можно сказать, что цепочка 01001 допускается определенной выше машиной, если на каждом шаге выбирается правильный путь. Вначале мы находимся в состоянии S. Прочитав первый 0, мы можем переключиться либо в состояние V, либо в Q; выбираем Q. Так как следующий символ 1, то третье состояние либо U, либо Q; вновь выберем Q.

 

Рис.2.3. Диаграмма состояний и ее НКА.

На следующей схеме показан полный разбор:

Теперь заметим, что для любой регулярной грамматики G можно построить диаграмму состояний и, следовательно, НКА. Диаграмма состояний может иметь любое число начальных состояний. Совершенно очевидно, что любое предложение грамматики G допускается этим НКА; говоря иначе, при работе НКА выполняется восходящий разбор. Как и в случае детерминированного автомата, для любого НКА можно найти регулярную грамматику G, предложения которой будут именно теми цепочками, которые допускаются НКА.

 

ПОСТРОЕНИЕ КА ИЗ НКА.

 

Итак, при работе НКА возникает проблема, которая заключается в следующем: мы не знаем, какую выбрать дугу на каждом шаге, если существует несколько дуг с одинаковой пометкой. Теперь покажем, как из НКА построить КА, который как бы параллельно проверяет все возможные пути разбора и отбрасывает тупиковые. То есть если в НКА имеется, к примеру, выбор из трех состояний X, Y, Z, то в КА будет одно состояние [XYZ], которое представляет все три. Напомним, что возможные состояния на каждом шаге работы НКА - это подмножество полного множества состояний и что число различных подмножеств конечно.

Т е о р е м а 2.1. Пусть НКА=(K, VT, M, S, Z) допускает множество цепочек L. Определим КА F'=(K', VT,M',S',Z') следующим образом:

1. Алфавит состояний K' состоит из всех подмножеств множества K. Обозначим элемент множества K' через [S₁,S₂,...,S_i], где S₁,S₂,..., S_i - состояние из K. (Допустим впредь, что состояния S₁,S₂,...,S_i расположены в некотором каноническом порядке таким образом, что, например, состояние из K' для подмножества {S₁, S₂}={S₂, S₁} - суть [S₁, S₂].)

2. Множество входных литер VT для F и F' одно и тоже.

3. Отображение M' определим как

M'([S_1,S₂,...,S_i], T)=[R₁,R₂,..., R_j],

где M({S1,S2,...,S_i}, T)={R₁,R₂,... R_j}.

4. Пусть S={S₁,...,S_n}. Тогда S'=[S₁,..., S_n].

5. Пусть Z={S_j,S_k,..., S_l}. Тогда Z'=[S_j,S_k,...,S_l].

Утверждается, что F и F' допускают одно и то же множество цепочек.

Рис.2.4. Диаграммы состояний.

 

П р и м е р 2.2. На рисунке (2.4) приведена диаграмма состояний НКА с начальным состоянием S и P и одним заключительным состоянием Z. Справа показана диаграмма состояний соответствующего КА, у которого начальное состояние [S,P], а множество заключительных состояний {[Z],[S,Z],[P,Z], [S, P,Z]}.

Заметим, что состояния [S] и [P,Z] можно исключить, так как нет путей, ведущих к ним. Таким образом, построенный КА не является минимальным - возможен автомат с меньшим числом состояний.

Отображение М (рис.2.4.а) Отображение M’(рис.2.4.б)

M(S,0)=P M’(S,0)=P

M(S,1)={S,Z} M’(S,1)=[S,Z]

M(P,0)=Æ M’(SP,0)=[P, Æ]=P

M(P,1)=Z M’(SP,1)=[S,Z]

M(Z,0)=P M’(P,0)= 

M(Z,1)=P M’(P,1)=Z

M’(PZ,0)=P

M’(PZ,1)=PZ

M’(SZ,0)=P

M’(SZ,1)=[SPZ]

M’(SPZ,0)=P

M’(SPZ,1)=[SPZ]

M’(Z,0)=P

M’(Z,1)=P

 

НИСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ.