Зак. Ома в интегральной форме.

(обобщенный закон)

I=(j₂ - j ₁)/R=U/R

R= r ´(l/S) для цилиндрич проводников.

r - удельное сопротивление.

U=j₂ - j ₁ совпадают только для однородного участка цепи.

На осн. зак. сохр. энерг. можно получить зак. Ома в

общей форме, из которого следуют частные случаи.

Обобщенный закон Ома -

закон для неоднородного участка цепи.

Неоднородный участок - участок содержащий источник тока.

 

 

I=((j₂ - j ₁)±e)/R_{1,2 -} обобщенный закон.

R_1,2=R+ r

Со знаком + e берется тогда кокда сила тока от + к -.

Со знаком - e тогда когда о - к +.

(j₂ - j ₁)±e =U

Рассм. частный случай.

1) случай e=0

I=(j₂ - j ₁)/R=U/R

2) случай: замкнутая цепь

j₁=j₂ j₂ - j ₁=0

3) I=e/(R+r)

Зак. Ома в дифференциальной форме.

Рассм. проводник переменного сечения.

 

 

Выделим внутри элементарный объем, длинна - dl, площадь поперечн. сечения dS.

dR= r ´(dl/dS)

Выделим объем соответствующей однородному участку цепи.

dI=dU/dR

dI=dU/(r ´(dl/dS))

dI/dS=(1/ r)´(dU/dl)

j=(1/ r)´E

1/ r =g - удельная проводимость.

_ _

J=gE плотность тока в данн. точке проводника = произведению удел. Проводимости этого проводника на напряженность в этой же точке. C учетом сторонних сил для неоднородн. участка цепи зак. Ома будет:

_ _ _

j=g(E+E*)

Лекция.

Дополнительные оапределения Э.Д.С.

Для замкн. цепи зак. Ома будет

I=e/(R+r)

III) e=IR+Ir

IR - падение внеш. напряжения.

Ir - падение внутр. напряжения.

Электродвижущая сила источника тока = сумме падений напряжения на внеш. сопр. и на внутр. участке.

Из III можно прийти к заключению что если R>>r (источник тока разомкнут) R®¥.

IV) e=IR Э.Д.С.= напряжению на клемах разомкнутого тока.

Газовый разряд.

Ионизация. Рекомбинация газов.

Газы явл. диэлектрками, и в обычных условиях не проводят эл. ток.

Все газы сост. из нейтральных атомов и малекул.

Если каким либо образом создать носители тока в газах, то они станут проводниками.(ионизация).

: УФ, R - лучи, g - изл., a, b частицы - внешние ионизаторы.

Ионизация - это превращение нейтральных атомов и малекул в ионы.

Электроны в атомах удерживаются силами куллоновск. притяжения.

Для удаления электрона необходимо сообщить энергию равную или превышающую энергию его связи с ядром (инергия ионизации E_i).

E_i =от 5 до 20 эВ

 

 

Электрон и ион могут перемещаться под действ. эл. поля.

Свободн. электроны сталкиваясь с нейтральными атомами может войти в его состав создавая отрицательный ион.

В результате ионизации возник. 3 вида носителей тока: +ион, -ион, электрон.

Возникают два направленных друг к другу встречных потока образующие эл. ток.

Одновременно с ионизацией в газе происходит рекомбинация газа заключающаяся в исчезновении носителей тока.

Под действием внешнего ионизатора мощностью Dn.

(показавает сколько электронов образуется в 1 м³ за 1с.)

1) В нач. момент времени И>Р.

2) Спустя некоторое время И=Р n₊=n_ устанавливается равновесие концетрации носителей тока n.

3) После выключения. И<Р

спустя время t n=0.

При выполнении ситуации 2) прохождение эл. тока через газы назв. газовыми разрядами.

Число рекомбинирующих ионов в единицу времени в 1м³ оказывается пропорциональным концентрации полож. и отр. Ионов.

Dn_r = rn² r - коэфф. рекомбинации.

В ситуации 2 Dn_i =Dn_r

Dn_i = rn²

1) n=Ö(Dn_i /r)

Различают два вида газовых разрядов.

1) несомостоятельный

2) самостоятельный.

Несамостоятельный разряд - такой разряд для поддержки которого необходим внеш. ионизатор.

Самостоятельный разряд - разряд без внешнего ионизатора.

Вольтамперная характеристика газового разряда.

Зак. Ома для газового рязряда.

Прохождение тока через газы удобно изучать с помощью схемы.

 

Для того чтобы существовал ток для газового ионизатора нужен внеш. ионизатор.

 

 

В области 1 с увеличением U прямо пропорционально растет сила тока.

В области 1 справедлив закон Ома для газов.

В обл. 2 наблюдается отклонение от прмолин. завис. и от зак. Ома.

Обл. 3 - обл. насыщения: все носители тока падают на электроны.

Обл. 1 - обл. слабых полей.

j=j₊+j_ j+q_элn₊<u₊>i

В равновесии q_эл(+)=(-)=e в силу преимущества однократной ионизации.

n₊=n_=n

j=en(<u₊>+<u_>)

Опыт показывает что скор. напр. движ. зависит от вел. напряженности эл. поля и подвижности.

u₊=b₊E

u_=b_E

u₊,u_ - подвижность носителей тока.

u₊>b_ b=u/E

Подвижность - это физ. вел. числ. = скор. упорядоч. движ. носителей тока под действием эл. поля единичной напряженности.

[b]=м²/(В´с)

1) j=e´n(b₊+b_)E - зак. Ома.

Произведение равновесной концентрации на элементар. заряд носителей тока на сумму подвижностей и на напр. эл. поля.

2) j=gE

g = e´n(b₊+b_) g=1/ r

g - удельная проводимость

3) j_н=e´Dn_i´d

d - расст. между электродами.

Dn_i - мощность ионизатора.

Ударная ионизация.

Самостоятельный газовый разряд.

При больших напр. поля свобод. электроны ускоряются до таких энергий которых достаточно для электронным ударом.

 

 

В обл. 4 в нутри газа появл. собственный источник ионизации, ударной ионизации.

Число электронов резко возрастает.

Лавинообразный процесс.

В обл. 4 наличие внеш. ионизации необходимо для поддеожания заряда.

При дальнейшем увеличении напр. поля в обл. 5 энергию достаточную дляионизации получают ионы.

В обл. 5 разряд становится самостоятельным. при этом сила тока увелич. Практически без изменения Е.

Напряженность при котор. происпереход из несомост. В самост. разряд. разряд назв. напряжением зажигания или пробоя.

Типы самостоятельных газовых разрядов.

1) тлеющий

2) искровой

3) дуговой

4) коронный

(в Трафимовой)

Зак. Джоуля - Ленца в интегральной и диффер. форме.

На внеш. сопротивлении в любой электрической цепи выделяется кол - во теплоты.

1) Q=I²Rt

За время t при протекании силы тока при протекании силы тока в нем выделится кол-во теплоты Q. (интегральная форма)

Получим зак. в диффер. форме.

Для этого рассм. внутри проводника с сопр. R элементарный объем dV=dS´dl

 

 

dR= r dl/dS

Запишем вместо 1) кол-во теплоты выдел. в этом объеме за время dt.

2) dQ=j´(dS)²´ r ´(dl/dS)´dt

(dQ/dVdt)= r j²

3) w_т= r j² j=gE

w_т = r ´g²E²=(1/g)g²E²

3¢) w_т =gE²

Работа и мощьность тока, КПД тока.

e=А*/q A=qe=eIt

полная мощность источника тока P=A*/t=Ie

P=I(IR­+Ir)=I²R+I²r

P=P_полез+P_{безполезн}

h=P_полез/P

Основные положения КЭТ.

1) При кристаллизации металлов из расплава атомы их теряют электроны. При этом возникают полож. заряж. ионы и свободные электроны. Если кажд. атом теряет по эл-ну, то n_ат=n_эл=(D/m)·N_a. Своб. эл-ны способны перемещаться по всему объёму металла.

2) Все металлы имеют кристаллич. структуру, в основе которой лежит кристаллич. решётка кубич. формы с положит. ионами в узлах. Таким образом решётка прозрач. для эл-нов.

3) Своб. эл-ны, оторванные от атомов, становятся коллективной собственностью всего металла. Они соверш. хаотич. тепл. движение. При этом эл-ны ведут себя подобно одноатомным мол-лам идеал. газа, подчиняясь статистике Максвелла. Своб. эл-ны принято назыв. “электронным газом”. Для эл-нов по ф-ле, известной из МКТ можно определить сред. скор. теплового движения:

áVтñ=Ö(8KT)/(pm)»10⁵м/c. 4) Своб. эл-ны, сталкиваясь с ионами, расположенными в узлах решётки, отдают им свою кинет. энергию. Этим обусловлено сопротивление проводников.

5) При приложении внешн. эл. поля напряжённостью E на хаотич. тепл. движение эл-нов накладывается упорядоченное движение. При этом возникает эл. ток. áVñ «áV_Tñ

Оценим áVñ по ф-ле j=q_элnáVñ=enáVñÞ

Þ áVñ=j/(en); n~10²⁹м^-3, j_(Cu)=10⁷А/м²Þ

Þ áVñ~10^-3м/с. Суммарн. скор.áV_Sñ=áVñ+áV_Tñ

Поскольку áVñ «áV_Tñ, то áV_Sñ» áV_Tñ

Закон Ома в КЭТ

Основные положения КЭТ позволяют вывести ф-лу закона Ома как ф-цию параметров носителей тока. Для вывода используем соотношение j=enáVñ. Пусть к проводнику приложено внешнее поле E. Своб. эл-ны придут в движение. На эл-ны будет действ. сила со стороны поля F=eE.E=constÞa=const.

F=eE=ma (по II з-ну Ньют.). a=(eE)/m

Для равноуск. движ. V_t=V₀+at

ср. длина своб. пробега álñ~d расст. между ионами; t-время своб. пробега.

Скорость электрона

V_t=V_max=at - до столкновения с ионом

V₀=0 - после столкновения с ионом

áVñ=(V₀+V_max)/2=V_max/2=(at)/2=(eEt)/2m;

t = álñ/áV_Sñ = álñ/áV_Tñ;

áVñ = [(eE)/2m] · álñ/áV_Tñ;

j=enáVñ=[(e²nE)/2m]·álñ/áV_Tñ з-н Ома в КЭТ

j=gE Þ g=(ne²álñ) / (2máV_Tñ)

Закон Джоуля-Ленца в КЭТ

Нагревание проводника, согласно КЭТ, объясняется столкновением электронов с ионами кристал. решётки. Рассчитаем кинет. энергию отдельного эл-наперед столкновением с ионом, полученную им за счёт поля: W₁=(mV²_max)/2.

За 1 сек. эл-н может испытывать Z соударений, где Z = 1/t =áV_Tñ / álñ. Если в 1 м³ число эл-нов = n, то кинет. энергия, переданная решётке всеми n эл-нами за Z столкновений каждого из них W=náZñW₁=w_T.

w_T=[(mV²_max)/2]·n·áZñ=[ne²álñ/2máV_Tñ]E²

Затруднения КЭТ

1) Температурная зависимость проводников. Согласно экспер. данным сопр. металлов увелич. с температурой по з-ну R=R₀+aT, где R₀-сопр. при T=273K, a=1/273 град^-1. Для r ф-ла аналогична r=r₀+aT. Согл. опыта r~T. r=2máV_Tñ/(ne²álñ)Þr~áV_Tñ. На осн. КЭТ след. r=ÖT, т.е. теория расходится с опытом.

2) Теплоёмкость металлов и диэлектриков. Согл. опвтов атомная теплоёмк. металлов и диэл-ков одинакова (C=3R, где R-газовая постоянная). Это положение наз. з-н Дюлонга и Пти. Согл. КЭТ металл сост. из кристал. решётки и своб. эл-нов, а диэлектрик своб. эл-нов не имеет. Следует ожидать, что теплоёмк. металлов=т.ё. кристал. решётки+т.ё. своб. эл-нов (C_мет=R+3/2R=4,5R), чего нет на опыте.

Электронный газ, на самом деле подчиняется не классической статистике Максвелла, а квантовой статистике. Затруднения устраняются в квантовой теории проводимости. Несмотря на затруднения, КЭТ она проста и широко применяется при высоких темп-рах и малых концентрациях.

Электромагнетизм

Магн. поле. Движ. заряды в окруж. пространстве создают магн. поле, которое явл. одной из форм сущ. материи. В отличие от эл. статического поля, магнитное действует только на движ. заряды. Проводники с текущими по ним токами в окруж. пр-ве создают магн. поле. Принято различать макро - и микротоки. Макротоки -это токи, текущие по проводникам. В любом вещ-ве электроны движутся по круговым орбитам. Движение эл-нов в атоме по круговым орбитам тоже приводит к созданию магн. поля. Токи, создаваемые в веществах движущимися эл-нами называют микротоками.

Гипотеза Ампера: в каждом вещ-ве за счёт движения электронов возникают микротоки.

Для исслед. магн. поля применяют магн. стрелки (опыт Эстерда). Магн. стрелка предст. собой магнит, одетый на остриё. При пропускании тока через проводник стрелка испытывает силовое воздействие (устанавливается перпенд. проводнику). 2^й метод исслед. маг. поля - с помощью плоского контура с током. Форма контура не играет роли.

Необходимо, чтобы размер контура был настолько мал, чтобы не искажал исследуемое поле. Контуры, вносимые в магн. поле испытывают ориентирующее действие со стороны этого поля. Рамки принято характеризовать положит. нормалью. Положительной наз. нормаль, проведённую к центру проводника, удовлетворяющего правилу правого винта по напр. тока. На основании действия сил на рамку делают вывод: магнитное поле - силовое и его надо характеризовать опред. направлением. За напр. магн. поля принимают напр. полож. нормали в данном месте распол. контура с током.

Определение характеристик маг. поля связано с определением поведения контура с током в поле. В однор. поле внесён контур тока таким образом, чтобы вдоль линий поля была направлена плоскость.

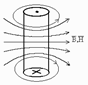
Пара сил создаёт вращающий момент M. Опыт показывает, что вращ. момент зависит от некот. силовой хар-ки поля и от силы тока в рамке (M~B; |M|~|I|). Для всех рамок вводится хар-ка, связанная с размерами расок и силой тока, текущей в них. P_m - магнитный момент. P_m=I·S [А·м²]. Магн. момент явл. вектором. P_m=n·I·S, где n - орт полож. нормали, т.е. P_m || n. Опыт показ., что M=[P_m , B] - механический вращ. момент равен векторному произведению магнитного момента рамки на вектор индукции магн. поля. M=P_m·B·sina (a=P_m^B). Из этой ф-лы видно, что M=max, если a=90° (положение I на рис.) M_max=P_m·B(1). M=0 при a=0 (полож II). Полож. II соответствует устойчивому равновесию рамки.

Индукция магн. поля - основная силовая хар-ка этого поля. Согл. ф-лы (1) B=M_max / P_m. Индукцией магн. поля в данной точке наз. физическая величина, численно равная макс. вращающему моменту, действующ. в данной точке на рамку с током, имеющую единичный магн. момент. [B]=Н/(А·м)=Тл (Тесла). Ин-ция магн. поля предст. собой хар-ку результирующего поля, созданного макро- и микротоками. Индукцию можно изобразить силовыми линиями (аналог напряжён. эл. стат. поля).

Напряжённость магн. поля

Использ. вектор B не всегда удобно, поскольку проявл. зависимость от свойств Среды. Вводится вспомогат. хар-ка, не завис. от свойств Среды - напряжённость магнитного поля H (аналог D в эл. статике). B=mm₀H, где m-магн. проницаемость. Для вакуума m=1. m₀-магнитная постоянная. m₀=4p·10⁷ Гн/м. [H]=А/м. Для вакуума H=B/m₀. За ед. (А/м) напряж. магн. поля принимают напряж. такого поля, у которого индукция B=4p·10⁷Тл. H определяется только макротоками и не завис. от микротоков. Поскольку H - это вектор, для него принято строить линии напряжённости.

Вихревой характер маг. поля. В отличие от эл. стат. поля, маг. поле является вихревым: линии магн. поля всегда замкнуты, представляют собой окружности (вихри), охватывающие проводники с током.

Магн. поле не явл. потенциальным. Линии поля B строят согласно правилу правого винта. Векторы B и H направлены по касательной в каждой точке линий.

Принцип суперпозиции

Магнитных полей

Если в пр-ве имеется неск. проводников с токами, то в каждой точке пр-ва магн. поле создаётся каждым из проводников в отдельности независ. от наличия остальных. Результир. поле в этой точке характеризуется векторами B и H. B_i и H_i - векторы, порождаемые i-ым проводникомс током.

B=SB_i; H=SH_i;

Закон Био-Савара-Лапласа

Осн. задача магнитостатики состоит в умении рассчит. хар-ки полей. Закон Б-С-Л с использованием принципа суперпозиции даёт простейший метод расчёта полей.

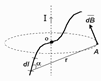
dB-индукция, созд. в точ. A.

dB=(mm₀ /4p)·(I·dl·sina/r²) [1]

dH=(I·dl·sina)/(4pr²) [2]

Индукция магн. поля, созданная элементом проводника dl с током I в точке A на расстоянии r от dl пропорц. силе тока, dl, синусу угла между r и dl и обр. пропорцион. квадрату расстояния r.

___ ____ __

dB=(mm₀ /4p)·(I·[dl,r] /r³)

Значение з-на Б-С-Л заключается в том, что зная dH и dB от dl можно вычислить H и B проводника конеч. размеров разл. форм.

Применение з-на Б-С-Л

Поле прямого отрезка конечной длины с током.

m=1, m₀=4p·10^-7Гн/м, H?, B?

dH=I·dl·sina/4pr²

По правилу прав. винта найдём направл. dH

____ ____

H=SdH. Поскольку все dH напр. одинаково, можно записать H=òdH. Переменной интегрирования выби-раем угол a.

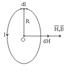
rda/dl=sina Þ dl=rdl/sina.

dH=I·r·da·sina/sina·4pr²=

=I·da /4pr

из треуг. DOAÞ b/r=sinaÞ

Þr=b/sina.

dH=I·sinada/4pb

a1

H=ò I·sinada/4pb=

a2

a1 a1

=I/4pbò sinada=-I/4pbcosa|

a2 a2

H=I/4pb(cosa₁-cosa₂) (2)

B=m₀I/4pb(cosa₁-cosa₂) (2’)

Поле прямого бескон. тока.

Для беск. тока a₁=0, a₂=p

В (2): cosa₁-cosa₂=1-(-1)=2

H=I/2pb; B=m₀I/2pb.

Поле кругового тока

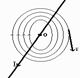
H=òdH; r=R; a=90°

2pR

H=ò I·dl/4pR²=I·2pR/4pR²=

=I/2R; B=Im₀/2R (4)

Картина линий поля для кругового тока:

Поле подобно эл. статич. полю диполя. В связи с этим круговой ток пердст. собой магн. диполь. Покажем, что круг. ток может служить магн. диполем. Для этого в ф-ле (4) домножим числитель и знаменатель на pR².

B=m₀·I·4pR²/2RpR²

pR²=S; I·S=P_m

B=m₀·P_m /2pR³

Закон Ампера

На опыте устан., что на проводник с током в магн. поле действ. сила. Для прямолин. проводников длиной l: F=IBl·sina. При a=90° F=IBl. Для проводников сложной формы з-н Ампера запис. в дифференц. форме: dF=IBdl·sina;

___ ___ ___

dF=I[B,dl]-векторная форма.

____ ____

F=SdF

Взаимод. паралл. токов

Рассм. 2 проводника, расположенных паралл. друг к другу.

Будем считать, что 1 создаёт магн. поле, а 2 находится в поле 1-го. Тогда индукция маг. поля B₁ в точках нахождения 2: B₁=m₀I₁/2pd.

F₂=I₂B₁l₂sina=mI₁I₂l₂/2pd.

Можно аналог. рассм. силу F₁, действующ. на проводник 1 со стороны поля тока I₂. F₁=F₂, если l₁=l₂=l. Парал. токи притягиваются, антипарал. - отталкиваются.

При рассм. парал. проводников вводят силу, действ. на единицу длины проводника:

f_ед.дл.=m₀I₁I₂/2pd. (1)

Эта ф-ла позвол. ввести единицу силы тока в СИ “1 Ампер”.

Опред. ед. силы тока-Ампер

Полагая, что I₁=I₂=I из (1) имеем: I²=f_ед.дл.·2pd/m₀= f_ед.дл.·d/2·10^-7. Берём d=1м, f_ед.дл.=2·10^-7Н/м.

За единицу силы тока 1A приним. силу такого тока, который протекает по 2-м парал. проводникам, расп. на расст. 1 м в вакууме, вызывает силу взаимодействия между ними, равную 2·10^-7Н на кажд. ед. длины.

Сила Лоренца.

Эл. ток предст. собой упорядоченн. движение эл. зарядов. На токи в магн. поле действует сила Ампера, т.е. со стор. магн. поля на кажд. носитель заряда действ. тоже сила. Эту силу наз. силой Лоренца.

____ ____

F_л=qVBsina; a=B^V

___ _ ____

F_л=q[V,B] - в вект. форме.

На покоящеиеся заряды сила Лоренца не действ. На заряды, влетающие в поле паралл. линиям поля сила Лор. тоже не действ.

Если одноврем. действ. электр. и магн. поля, то справедлва ф-ла Лоренца:

-___ ___

F=qE+F_л