
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение допустимой скорости движения транспортера грузоподъемностью 220 т по пролетному строению моста длиной 55 мСодержание книги
Поиск на нашем сайте
Элемент В0—В2. Минимальный класс элемента
Тогда допустимая скорость движения поезда (см. рисунок 4.1.) составляет Элемент В2—В4. Минимальный класс элемента по прочности Элемент В4—В5. Минимальный класс элемента по прочности Таким образом, минимальная скорость движения поезда, состоящего из электровоза серии ВЛ10У и 16-осного транспортера грузоподъемностью 220 т с вагонами прикрытия и 4-осных вагонов по пролетному строению длиной 55 м, составляет 25 км/ч (см. таблицу. П.А.1)
Приложение Б. Определение эквивалентной нагрузки от классифицируемого подвижного состава (Обязательное) Эквивалентные нагрузки от классифицируемого подвижного состава
или
или
Где При определении эквивалентной нагрузки Невыгоднейшее положение нагрузки на пролетном строении находят по правилам: а) для линии влияния с вершиной в начале и конце длины загружения (α=0,0) невыгоднейшее загружение определяют по формуле
Где Рi — первый груз (наиболее тяжелый), поставленный над вершиной линии влияния, тс; Р2, Р3 … — остальные грузы на линии влияния, тс; λ — длина загружения линии влияния, м; аk — расстояние между первым и вторым грузом, м. Если левая часть неравенства больше правой, то загружение является невыгоднейшим; если меньше, то всю систему грузов нужно передвинуть так, чтобы следующий груз был поставлен над вершиной линии влияния, и повторить проверку и т. д.; б) для линии влияния с вершиной в середине длины загружения (α=0,05) невыгоднейшее положение нагрузки должно удовлетворять следующим условиям:
или (Б.5.)
Описанные проверки невыгоднейшего положения груза справедливы только в том случае, если при перемещении груза из первоначального положения ни один из грузов не выходит за пределы линии влияния. Если в пределы линии влияния входит новый груз, то он должен учитываться при отыскании невыгоднейшего положения груза, а при наличии поезда, длина которого превышает длину линии влияния, необходимо делать ряд попыток для нахождения критического груза. При этом возможно, что будет найден не один критический груз, а несколько, и поезд несколько раз необходимо устанавливать в различные критические положения, чтобы выбрать такое, при котором k0 принимает максимальное значение. Примеры классификации подвижного состава приведены в приложении А.
ПРИЛОЖЕНИЕ В. Интенсивности эталонных нагрузок С1 и Н1 и соответствующие им величины динамических коэффициентов (обязательное)
Таблица П.В.1. Интенсивность эталонной нагрузки С1 и соответствующие ей величины динамического коэффициента
Примечание: Для промежуточных значений длин загружения l и промежуточных положений вершин линий влияния a = а / l £ 0,5, величину нагрузки kc следует определять по интерполяции. Таблица П.В.2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.83 (0.007 с.) |

 ,м
,м

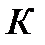



 , км/ч
, км/ч
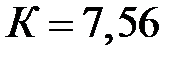 получен при расчете на прочность. Класс поезда с транспортером
получен при расчете на прочность. Класс поезда с транспортером  (см. п. 6.9.12). В связи с тем что
(см. п. 6.9.12). В связи с тем что  , пропуск заданной нагрузки без ограничения скорости невозможен. Класс поезда без динамики
, пропуск заданной нагрузки без ограничения скорости невозможен. Класс поезда без динамики  (см. п.6.9.12)
(см. п.6.9.12) ;
;  .
. км/ч.
км/ч. . Класс поезда с транспортером
. Класс поезда с транспортером  (см. п. 6.9.12),
(см. п. 6.9.12),  ;
;  м. Допускаемая скорость движения поезда составляет 50 км/ч.
м. Допускаемая скорость движения поезда составляет 50 км/ч. . Класс поезда с транспортером
. Класс поезда с транспортером  (см. п. 6.9.12),
(см. п. 6.9.12),  ;
;  м. Допускаемая скорость движения поезда составляет 50 км/ч.
м. Допускаемая скорость движения поезда составляет 50 км/ч. вычисляют при невыгоднейшем положении подвижного состава
вычисляют при невыгоднейшем положении подвижного состава (Б.1.)
(Б.1.) при
при  (Б.2.)
(Б.2.) при
при  (Б.3.)
(Б.3.) — нагрузка от оси на рельсы, тс;
— нагрузка от оси на рельсы, тс;  — ордината линии влияния под грузом
— ордината линии влияния под грузом  — площадь загружаемой линии влияния, м или м2;
— площадь загружаемой линии влияния, м или м2;  — расстояние от груза
— расстояние от груза  до ближайшего конца линии влияния с нулевой ординатой, м.
до ближайшего конца линии влияния с нулевой ординатой, м. классифицируемая нагрузка располагается относительно линии влияния в невыгоднейшее положение, при котором воздействие ее будет наибольшим. При этом один из грузов, называемый критическим Ркр, располагают над вершиной линии влияния.
классифицируемая нагрузка располагается относительно линии влияния в невыгоднейшее положение, при котором воздействие ее будет наибольшим. При этом один из грузов, называемый критическим Ркр, располагают над вершиной линии влияния. (Б.4.)
(Б.4.) ;
; 
 ;
; 



