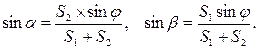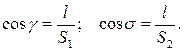Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Окремі випадки, що трапляються при перенесенні проекту в натуруСодержание книги
Поиск на нашем сайте
При перенесенні проекту в натуру, особливо в умовах пересіченої місцевості із значним нахилом, нерідко виникають труднощі (перешкоди), які потрібно долати, не вдаючись до будь–яких складних обчислень, а користуючись простими прийомами обчислень за допомогою логарифмічної лінійки безпосередньо в польових умовах. У ряді випадків при перенесенні проекту в натуру виникає необхідність виміряти лінію між точками А і В, щоб перенести на неї проектні точки. Якщо на цій лінії розташовані споруди, але між точками А і В є взаємна видимість, то цю перешкоду можна обійти, виносячи частину лінії за перпендикулярами на вільне місце, а потім повернутися у створ лінії АВ. Перпендикуляри можна побудувати екером, при цьому, чим коротший перпендикуляр d, тим точнішим буде рівняння: АВ = а + b + с. Якщо видимість між точками А й В відсутня, то на рівних відстанях від точки А вибирають дві допоміжні точки а і b, з яких можна побачити точку В. відрізки cd і c'd', одержують на місцевості положення точок d і d '. Нерідко при перенесенні проекту в натуру виникає необхідність знайти точку в створі лінії АВ, коли між точками А і В немає взаємної видимості або коли точки А і В знаходяться далеко одна від одної. Для розв’язання вказаної задачі на місцевості поблизу створу лінії АВ намічають точку С і вимірюють відстані АС = S1 і ВС = S2 і кут φ. Ці три величини дають можливість визначити відстань l від точки С до створу лінії АВ, що дорівнює CD. Позначимо кути біля точок А і В через α й β. Із рисунка видно, що: l = S1 sin α = S2sinβ. Оскільки величина l мала порівняно з АВ, то S1 + S2 можна вважати рівними АВ, тоді:
Підставляючи ці значення у формулу, матимемо:
Величину l легко обчислити на логарифмічній лінійці. Для одержання точки D величину l відмірюють від точки С, при цьому навіть значне відхилення напряму CD від перпендикуляра до лінії АВ дає дуже малу похибку визначення створу лінії АВ. Однак напрям CD легко одержати закутами α і σ, що дорівнюють:
Побудувати їх у точці С можна з точністю у кілька десятків мінут, оскільки відстань l – мала величина. Кути γ і σ можна одержати з вищою точністю, обчисливши кути α і β за формулами, наведеними нижче. Прорубування просік. При перенесенні проекту в натуру виникає потреба у прорубуванні просіки в лісосмугах або чагарниках. Коли ці просіки є лініями теодолітних ходів, усі необхідні геодезичні дані (кути і довжини ліній) обчислюють заздалегідь, тому під час роботи на місцевості особливих труднощів не буває. Коли ж положення проектних ліній визначають лише за лінійними промірами, напрямок просіки доводиться встановлювати в полі. У ряді випадків потрібно відразу ж мати досить точний напрямок, щоб не робити надмірно широких просік, не затрачати часу на вирівнювання їх і тощо.
Питання для самоконтролю 1. Назвіть основні особливості при перенесенні проекту в натуру згідно з матеріалами аерофотознімання. 2. За допомогою якого способу розподіляють нев’язку в натурі? 3. Які заходи необхідно застосовувати для забезпечення паралельності та перпендикулярності проектних ліній? 4. Які існують форми контролю обчислень при здійсненні землевпорядного проектування? 5. Назвіть основні способи перенесення об’єктів у натуру.
Питання на самостійну підготовку 1. Особливості перенесення у натуру проектів планування сільських населених пунктів 2. Якими методами здійснюється 3. Обхід місця, недоступного для постановки межевого знака. 4. Обхід перешкод при прокладанні проектного теодолітного ходу
Лекція 12 ТОЧНІСТЬ ГЕОДЕЗИЧНИХ РОБІТ У ЗЕМЛЕУСТРОЇ План Точність проектування площ ділянок аналітичним способом і порівняльна точність проектування різними способами Точність запроектованих ділянок, перенесених у натуру 3. Точність визначення площ землекористування з урахуванням похибок вимірювань на місцевості й на плані (карті) Питання для самоконтролю Питання на самостійну підготовку
|
|||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 127; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.115 (0.008 с.) |

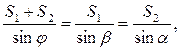 звідки:
звідки: