
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точність обчислення площ графічним способом і палеткоюСодержание книги
Поиск на нашем сайте
При розбивці ділянки на найпростіші фігури можна застосувати багато варіантів, проте точність обчислення площі ділянки при різних варіантах не буде однаковою. Похибку визначення площі кожного трикутника за висотою й основою можна обчислити за формулою (4.11). вона справедлива також і для прямокутника, паралелограма й трапеції, площі яких обчислюють за двома величинами, визначеними за планом. Похибки вимірювання ліній за планом можна вважати однаковими незалежно від довжин ліній:
тоді за формулою (4.11):
Оскільки для трикутника ah = 2Р, а для інших фігур a1h1 = Р, то згідно (а) для трикутника:
а для прямокутника, паралелограма й трапеції:
Якщо а = h, то для трикутника:
для прямокутника і паралелограма (при а1 = h1), а також трапеції при рівності середньої лінії й висоти:
Основу визначають точніше, ніж висоту, тому що на вимірювання висоти крім похибки визначення на плані, буде додатково впливати похибка проведення основи між вершинами кутів, до якої вимірюється висота. Проте вплив цієї додаткової похибки на похибку визначення висоти незначний, якщо трикутник рівнобедрений. Якщо ж трикутник близький до прямокутного, то похибка висоти в 1,2 раза більша від похибки основи. Похибка визначення відстані за планом m=0,008 см. Але враховуючи, що при розбивці фігури на трикутники не завжди вдається одержати трикутники з рівними основами й висотами, то похибку площі ділянки можна обчислювати за формулою (4.18):
або для планів різних масштабів:
де М – знаменник чисельного масштабу плану. Площу кожного трикутника контролюють, визначаючи її двічі з незалежних висот та основ, і з двох результатів виводять середнє арифметичне. Тоді похибка площі ділянки буде в √2 разів менше, ніж це дає формула (4.21). Гранична похибка визначення площі буде в три рази більшою від середньоквадратичної, а для одержання граничної (допустимої) розбіжності між двома значеннями площі треба потроєну середньоквадратичнупохибку ще збільшити в √2 разів, тому на основі (4.21) матимемо формулу (4.16):
Для підвищення точності визначення площі ділянки при обчисленні площ трикутників доцільно основи брати з результатів вимірів на місцевості (горизонтальні прокладення), якщо ці виміри проводили.
Точність однократного визначення площ квадратною і паралельною палетками, а також ротаметром у середньому характеризується емпіричною формулою:
Якщо площу контура (полігона) обчислюють за графічними (фотограмметричними) координатами точок, то похибка визначення площі може бути обчислена за формулою, в якій mt – помилка визначення графічних (фотограмметричних) координат у сантиметрах на плані. Наприклад, середньоквадратична похибка визначення координат вимірником за масштабною лінійкою дорівнює 0,018 см. Фотограмметричнийспосіб дає змогу визначати координати з похибкою 0,005 см і менше.
2. Точність визначення площі планіметром
Відносна середньоквадратична похибка визначення ціни поділки планіметра mp /p при чотириразовому обводі трьох квадратів координатної сітки близька до 1:1000 і впливає на похибки визначення площі незалежно від розміру фігури, яку обводять та кількості обводів цієї фігури. Похибка визначення кількості поділок mu є результатом впливу похибок: 1) відліків за лічильним роликом; 2) обводів; 3) механічного (тертя); 4) несумісності обвідного індексу з вихідною точкою на початку і в кінці обводів. Середньоквадратична похибка відліку становить 0,5 поділки. Для одного обводу, одержуваного як різницю відліків, вона дорівнює 0,5х√ 2 = =0,7 поділки і не залежить від розміру обвідної фігури. Друга і третя похибки приблизно однакові і можна прийняти, що їхній вплив пропорційний до кореня квадратного з площі обвідної фігури. Четверта похибка буде найменшою, коли при початковому положенні планіметра важелі утворюють кут, близький до прямого, за величиною вона приблизно вдвічі менша від похибок відліку і також не залежить від розміру фігури. Тому середньоквадратична похибка визначення площі при одному обводі не може бути меншою 0,7 поділки планіметра і відносно середньоквадратична похибки не може бути меншою 1: 1000. Загальну середньоквадратичну похибку для одного обводу при нормальній довжині обвідного важеля 150 – 170 мм можна обчислити за емпіричними формулами з площею до 200 см2 на плані:
а понад 200 см2:
|
|||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.98.40 (0.009 с.) |

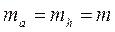
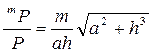 (а)
(а)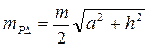 (б)
(б)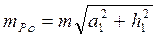 (в)
(в)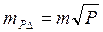 (4.17)
(4.17)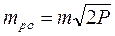 (4.18)
(4.18)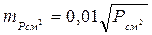
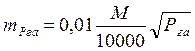 , (4.21)
, (4.21)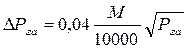
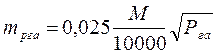 (4.22)
(4.22)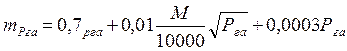 (4.26)
(4.26)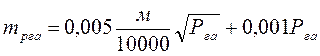 (4.27)
(4.27)


