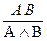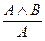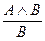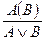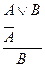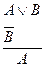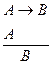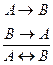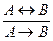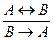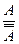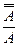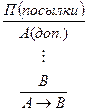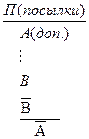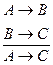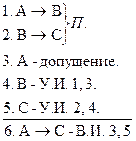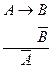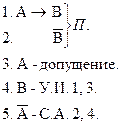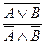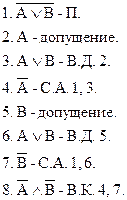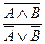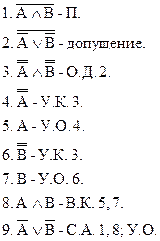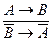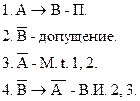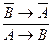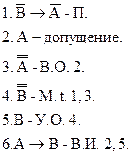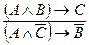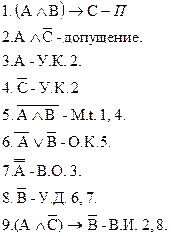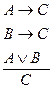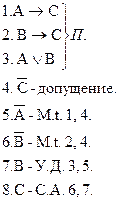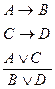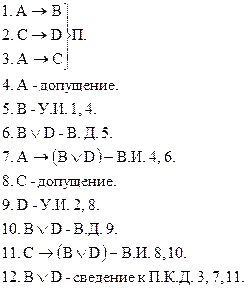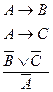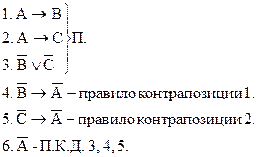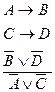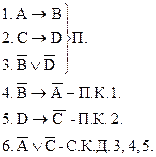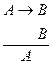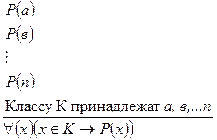Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила выводов логики высказыванийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Логика высказываний – это логическая система, которая анализирует процессы рассуждения, опираясь на истинностные характеристики логических связок и отвлекаясь от внутренней структуры суждений. Логика высказываний может строиться табличным методом или как исчисление, т.е. как система, позволяющая получать одни выражения из других на основании известных правил. Последняя называется системой натурального вывода. Аппаратом в ней служат правила вывода, каждое из которого является элементарной формой умозаключения. Правила вывода – это предписания или разрешения, позволяющие из суждений одной логической структуры как посылок вывести суждение некоторой логической структуры как заключение. Их особенность заключается в том, что признание истинности заключения производится на основании не содержания посылок, а их структуры. Правила вывода записываются в виде схемы, которая состоит из двух частей (верхней и нижней), разделенных горизонтальной линией – над чертой выписываются логические схемы посылок, под ней – заключение. Схема правил вывода:
Читается: из посылок вида Правила выводов логики высказываний делят на основные и производные. Основные правила – более простые и очевидные. Производные выводятся из основных. Их введение сокращает процесс вывода.
Как основные, так и производные делятся на прямые и непрямые (косвенные). Прямые правила указывают на непосредственную выводимость некоторых суждений из других суждений. Непрямые (косвенные) правила выводов дают возможность заключить о правомерности некоторых выводов из правомерности других выводов. Основные прямые правила: Правила введения и удаления конъюнкции (В.К.), (У.К.): В.К.
У.К.
Правила введения и удаления дизъюнкции (В.Д.), (У.Д.): В.Д.
У.Д.
Правила удаления импликации (У.И.):
Правила введения и удаления эквивалентности (В.Э.), (У.Э.): В.Э.
У.Э.
Правила введения и удаления двойного отрицания (В.О.), (У.О.): В.О. У.О. Основные непрямые правила Правила введения импликации (В.И.) и сведения к абсурду (С.А.): В.И.
С.А.
Производные правила Правило условного силлогизма
Доказательство:
Правило «modus tоllens»:
Доказательство:
Правило отрицания дизъюнкции (О.Д.):
Доказательство:
Правило отрицания конъюнкции (О.К.)
Доказательство:
Правила контрапозиции: 1. Доказательство:
2. Доказательство:
Правило сложной контрапозиции:
Доказательство:
Правило простой конструктивной дилеммы (П.К.Д.)
Доказательство:
Правило сложной конструктивной дилеммы (С.К.Д.)
Доказательство:
Правило простой деструктивной дилеммы (П.Д.Д.)
Доказательство:
Правило сложной деструктивной дилеммы (С.Д.Д.)
Доказательство:
Вопросы для повторения 1. Что такое отношение логического следования? Как проверить, имеет ли оно место в умозаключении? 2. Что такое непосредственные умозаключения и каковы их виды? 3. Назовите правила посылок и правила терминов простого категорического силлогизма. 4. Что такое метод натурального вывода? 5. Каковы основные прямые и непрямые правила логики суждений? 6. Чем отличается прогрессивный полисиллогизм от регрессивного? Недедуктивные (вероятностные) умозаключения Понятие о недедуктивных (вероятностных) умозаключениях Умозаключение, в котором заключение не следует строго логически из посылок, а лишь в некоторой степени подтверждается посылками, называется недедуктивным или вероятностным. Например:
Это умозаключение от утверждения следствия к утверждению основания по схеме: Между посылками и заключением нет отношения логического следования, что можно проверить с помощью таблицы истинности. По своему характеру вероятностные умозаключения весьма разнообразны. Это умозаключения по неправильным модусам категорического и условно-категорического силлогизмов, отдельные виды индуктивных умозаключений и умозаключения по аналогии. Индукция – это способ рассуждения, при котором заключение, являющееся общим рассуждением, получается на основе менее общего знания или отдельных фактов. Неполная индукция Неполная индукция – вероятностное умозаключение, в котором заключение о принадлежности признака целому классу предметов делается на основании принадлежности этого признака части предметов данного класса. Логическая структура неполной индукции может быть выражена следующим образом:
Виды неполной индукции: индукция через простое перечисление, статистическая индукция, индукция, основанная на установлении причинной связи. Индукция через простое перечисление (популярная индукция) – разновидность неполной индукции, в которой заключение о целом классе однородных предметов делается на том основании, что среди наблюдаемых случаев не встречалось факта, противоречащего производимому заключению. Индукция, основанная на простом наблюдении, распространена в быту: ласточки летают низко - быть дождю, если красный закат солнца, то завтра будет ветреный день и т.д. Степень вероятности заключения индукции через простое перечисление увеличивается с увеличением числа наблюдаемых случаев. Возможные ошибки, связанные с использованием этого вида умозаключения, получили название поспешного обобщения. Статистическая индукция – разновидность неполной индукции, содержащая информацию о частоте распределения некоторого свойства для определенного класса предметов. Этот класс предметов в статистике называется популяцией, а любой класс популяции – выборкой. Степень вероятности заключения статистической индукции зависит от того, насколько квалифицированно сделана выборка. Индукция на основе установления причинной связи (научная) – разновидность неполной индукции, в которой заключение о целом классе однородных предметов делается на основании знания необходимых, т.е. существенных признаков части предметов данного класса.
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 823; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.23 (0.01 с.) |

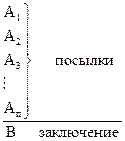
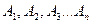 можно вывести заключение В.
можно вывести заключение В.