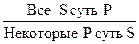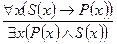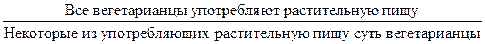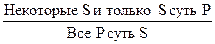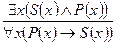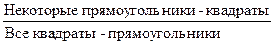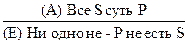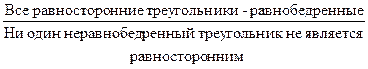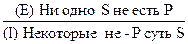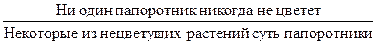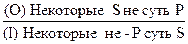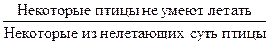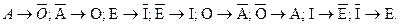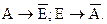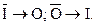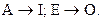Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выражение одних логических связок посредством другихСодержание книги
Поиск на нашем сайте
Рассмотренные выше логические союзы взаимозаменяемы и выразимы через другие. Например:
Существует метод проверки равносильности сложных суждений. Он заключается в построении таблиц истинности для соответствующих символических выражений. Если таблицы истинности совпадают при одинаковых логических значениях переменных, то такие выражения равносильны. Докажем равносильность следующей формулы
Таблицы истинности двух последних столбцов совпали, следовательно данные выражения равносильны. Вопросы для повторения 1. Дайте определение суждения. Какие суждения называются простыми, а какие сложными? 2. Какова логическая структура атрибутивных суждений и суждений отношения? 3. Каково отношение суждения и высказывания? 4. Чем определяется логическое значение (истинность или ложность) высказываний? Дедуктивные умозаключения. Выводы из простых суждений §1. Умозаключение как форма мышления. Виды умозаключений Умозаключение – форма мышления, посредством которой выводится новое суждение на основании одного или более известных суждений. Ранее известные, исходные суждения, из которых выводится новое суждение, называются посылками умозаключения, а новое суждение, полученное в результате сопоставления посылок – заключением. Например, в умозаключении
первые два суждения – посылки, а последнее – заключение. Логический переход от посылок к заключению называется выводом. Виды умозоключений 1. По характеру логического следования заключений из посылок все умозаключения делятся на дедуктивные (необходимые) и недедуктивные (выроятностные). Дедуктивные – умозаключения, между посылками и заключением которых имеет место отношение логического следования, которое можно определить следующим образом: из суждения α логически следует суждение β тогда и только тогда, когда α и β связаны по смыслу, а α→β является логическим законом. При этом α – символическое выражение посылок, соединенных логическим союзом конъюнкция, β – символическое выражение заключения. Умозаключение будет дедуктивным, если его символическое выражение будет представлять собой логический закон, т.е. тождественно-истинную формулу, что проверяется посредством таблицы истинности.
Тождественно-истинная формула – формула, принимающая логическое значение истины при всех вариантах логических значений входящих в нее переменных. Умозаключение, между посылками и заключением которого не имеет места отношение логического следования, называется недедуктивным или вероятностным. 2. В зависимости от количества посылок все умозаключения делятся на непосредственные и опосредствованные. Непосредственные умозаключения – умозаключения, заключение в которых выводится из одной посылки. Например, исходное суждение: «Все львы хищники», новое – «Ни один лев не является нехищником». Опосредствованные умозаключения – умозаключения, заключение в которых выводится из двух и более посылок. Например:
Непосредственные умозаключения К непосредственным умозаключениям относятся следующие виды: 1) превращение; 2) обращение; 3) контрапозиция (противопоставление предикату); 4) умозаключение по логическому квадрату. Превращение Превращение – такое непосредственное умозаключение, в котором устанавливается связь между понятием, являющимся субъектом исходного суждения, и понятием, противоречащим предикату исходного суждения. Например:
Исходное суждение – общеутвердительное (А) превращается в общеотрицательное (Е). Общеотрицательное (Е) превращается в общеутвердительное (А). Например:
Частноутвердительное суждение (I) превращается в частноотрицательное (О). Например:
Частноотрицательное (О) превращается в частноутвердительное (I). Например:
В результате операции превращения меняется качество суждения, но количество остается прежним. Обращение Обращение – такое непосредственное умозаключение, в результате которого субъект исходного суждения становится предикатом, а предикат – субъектом заключения. Например:
В зависимости от распределенности терминов исходного суждения различают два вида обращения:
1) простое (чистое) обращение; 2) нечистое обращение.
Простое (чистое) обращение имеет место в том случае, если оба термина (субъект и предикат) исходного суждения являются распределенными или оба являются нераспределенными. Например:
При чистом обращении А обращается в А:
Е обращается в Е:
Например:
I обращается в I:
Например:
Частноотрицательные суждения не обращаются с необходимостью.
Нечистое обращение представлено двумя вариантами: 1) обращение с ограничением; 2) обращение с приращением. Обращение с ограничением имеет место при переходе от общеутвердительных суждений (А) к частноутвердительным (I):
Например:
Обращение с приращением имеет место в случае выделяющих суждений и связано с переходом от частных суждений к общим:
Например:
Контрапозиция (противопоставление предикату) – непосредственное умозаключение, в результате которого в заключении субъектом становится понятие, противоречащие предикату исходного суждения, а предикатом – субъект исходного суждения. Противопоставление предикату представляет собой синтез превращения и обращения. Контрапозиция различных суждений производится по следующей схеме:
Частноутвердительное суждение контрапозицированно быть не может. Умозаключение по логическому квадрату Учитывая отношения между категорическими суждениями А, Е, I, О, которые продемонстрированы схемой логического квадрата, можно строить выводы, основываясь на истинности или ложности исходного суждения. Выводы строятся по схемам: Отношения противоречия (А – О; Е - I):
Отношение контрарности (противоположности) (А - Е):
Отношение подпротивности (I - О):
Отношение подчинения (А – I; Е - О):
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.49.19 (0.01 с.) |

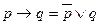 - импликация через дизъюнкцию
- импликация через дизъюнкцию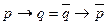 - импликация через импликацию
- импликация через импликацию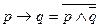 - импликация через конъюнкцию
- импликация через конъюнкцию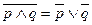 - конъюнкция через дизъюнкцию
- конъюнкция через дизъюнкцию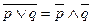 - дизъюнкция через конъюнкцию
- дизъюнкция через конъюнкцию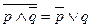 - конъюнкция через дизъюнкцию
- конъюнкция через дизъюнкцию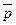
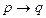
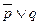
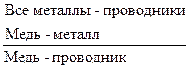
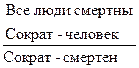
 .
.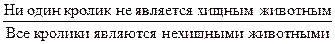 .
.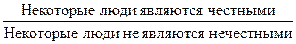 .
.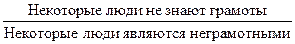 .
.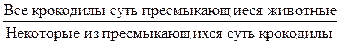
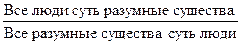 .
.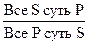
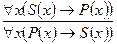
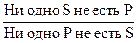
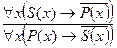
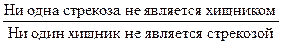 .
.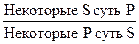
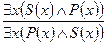
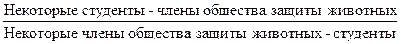 .
.