
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложные суждения и их виды. Понятие о логическом союзеСодержание книги
Поиск на нашем сайте Сложное суждение – суждение, образованное из простых посредством логических союзов конъюнкции, дизъюнкции, импликации, эквивалентности. Особенность сложных суждений заключается в том, что их логическое значение (истинность или ложность) определяется не смысловой связью простых суждений, составляющих сложное, но двумя параметрами: 1) логическим значением простых суждений, входящих в сложное, 2) характером логической связки, соединяющей простые суждения.
Современная формальная логика отвлекается от содержательной связи между простыми суждениями и анализирует такие высказывания, в которых эта связь может отсутствовать. Например, «Если квадрат гипотенузы равен сумме квадратов катетов, то на Солнце существуют высшие растения». Конъюнктивные суждения Конъюнктивное суждение – суждение, которое является истинным тогда и только тогда, когда истинны все входящие в него суждения. Образуется посредством логического союза конъюнкции, выражающегося грамматическими союзами «и», «да», «но», «однако». Например, «Светит, да не греет». Символически обозначается следующим образом:
Дизъюнктивные суждения Имеется два вида дизъюнктивных суждений: строгая (исключающая) дизъюнкция и нестрогая (неисключающая) дизъюнкция. Строгая (исключающая) дизъюнкция – сложное суждение, принимающее логическое значение истины тогда и только тогда, когда истинно только одно из входящих в него суждений. Например, «Данное число либо кратно, либо не кратно пяти». Логический союз дизъюнкция выражается посредством грамматического союза «либо…либо». Символически записывается
Нестрогая (неисключающая) дизъюнкция – сложное суждение, принимающее логическое значение истины тогда и только тогда, когда истинным является, по крайней мере, одно (но может быть и больше) из простых суждений, входящих в сложное. Например, «Писатели могут быть или поэтами, или прозаиками (или тем и другим одновременно)». Нестрогая дизъюнкция выражается посредством грамматического союза «или…или» в разделительно-соединительном значении. Символически записывается
Импликативные (условные) суждения Импликация – сложное суждение, принимающее логическое значение ложности тогда и только тогда, когда предшествующее суждение (антецедент) истинно, а последующее (консеквент) ложно. В естественном языке импликация выражается союзом «если…, то» в смысле «наверно, что р и не-q». Например, «Если число делится на 9, то оно делится и на 3». Символически импликация записывается
Анализ свойств импликации показывает, что истинность антецедента является достаточным условием истинности консеквента, но не наоборот. Достаточным для некоторого явления считается такое условие, наличие которого непременно вызывает это явление. В то же время истинность консеквента является необходимым условием истинности антецедента, но не достаточным. Необходимым для явления считается такое условие, без которого оно (явление) не имеет место. Суждения эквивалентности Эквивалентность – сложное суждение, которое принимает логическое значение истины тогда и только тогда, когда входящие в него суждения обладают одинаковым логически значением, т.е. одновременно либо истинны, либо ложны. Логический союз эквивалентности выражается грамматическими союзами «тогда и только тогда, когда», «если и только если». Например, «Если и только если треугольник равносторонний, то он и равноугольный». Символически записывается Логическое значение эквивалентности соответствует таблице истинности:
Эквивалентное суждение со связанными по содержанию членами выражает одновременно условие достаточное и необходимое:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

 , где p, q – переменные, обозначающие простые суждения,
, где p, q – переменные, обозначающие простые суждения,  - символическое выражение логического союза конъюнкции. Определению конъюнкции соответствует таблица истинности:
- символическое выражение логического союза конъюнкции. Определению конъюнкции соответствует таблица истинности: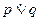 . Логическое значение строгой дизъюнкции соответствует таблице истинности:
. Логическое значение строгой дизъюнкции соответствует таблице истинности: . Нестрогой дизъюнкции соответствует таблица истинности:
. Нестрогой дизъюнкции соответствует таблица истинности: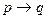 (если р, то q). Логическое значение представлено в таблице истинности:
(если р, то q). Логическое значение представлено в таблице истинности: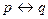 (если и только если р, то q).
(если и только если р, то q). . Равносильность выражений (
. Равносильность выражений (


