
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория активированного комплексаСодержание книги
Поиск на нашем сайте
Введение в уравнение для константы скорости реакции (43) стерического фактора не решило проблемы в теории активных соударений. Причина в отсутствии прямой корреляции между вероятностными факторами и вероятностью того, что реагирующие молекулы столкнуться определенными группами. В связи с этим большинство расчетов химической кинетики сегодня выполняются на основе теории абсолютных скоростей реакций (или теории активированного комплекса; или теории переходного состояния) – теории Эйринга. Теория Эйринга исходит из предположения, что неравновесным состояниям можно приписать определенные термодинамические свойства, и, что полная реакция складывается из повторяющихся элементарных актов. Каждый элементарный акт является результатом взаимодействия небольшого числа атомов или молекул, приводящего к образованию новой относительно устойчивой конфигурации. Под конфигурацией у Эйринга понимается система, т.е. определенное расположение взаимодействующих частиц в пространстве, с определенным распределением энергии между этими частицами и т.д. В простейшем случае это может быть расстояние между двумя частицами. Начальные и конечные состояния стабильны. Им соответствует относительный минимум энергии. Для того чтобы достигнуть конечное состояние исходя из начального, вся группа атомов должна пройти через промежуточные состояния, обладающие более высокой энергией по сравнению, как с исходным состоянием, так и по сравнению с конечным состоянием. В некотором промежуточном состоянии энергия достигает максимума. Конфигурация, отвечающая максимуму свободной энергии, получила название активированного комплекса (активированного состояния). Согласно Эйрингу, если активированное состояние достигнуто, существует большая вероятность того, что реакция пройдет полностью. Дополнительная энергия, необходимая для достижения активированного состояния, получила название энергии активации процесса Еэ. В простейшем случае реакция может состоять в сближении 2-х молекул вдоль прямой линии до тех пор, пока при некотором критическом расстоянии они не образуют активируемый комплекс М++.
А + В = М++ = Р + Q (44)
Исходные положения теории Эйринга состоят в следующем:
1. Полная реакция складывается из повторяющихся элементарных единичных актов, каждый из которых представляет собой переход из некоторой начальной конфигурации в конечную конфигурацию (состояние). Переход осуществляется путем непрерывного изменения конфигурационной координаты. Начальные и конечные конфигурации представляют собой стабильные состояния, котором соответствует относительный минимум энергетического рельефа, так что система в каждом из этих состояний стремиться вернуться в исходное положение, если ей сообщена малая энергия. 2. На любом пути реакции между начальным и конечным состояниями существует энергетический барьер, а наиболее предпочтительным путем реакции, обычно оказывается тот, для которого этот барьер наименьший. (Потенциальный рельеф свободной энергии) 3. На предпочтительном пути реакции между начальным и конечным состоянием существует критическая конфигурация, отвечающая максимуму свободной энергии. Эта конфигурация называется активированным комплексом (активированным состоянием). Если достигнуто активированное состояние, то существует большая вероятность, что реакция пройдет до конца. 4. В начальном состоянии реагирующие объемы находятся в равновесии с активированными комплексами, несмотря на то, что комплексы М++ не образуют равновесных состояний. 5. Активированный комплекс обладает всеми свойствами обычной равновесной конфигурации, за исключением того, что у него нет степени свободы, отвечающей колебательному движению по пути реакции. Исходя из вышеизложенных положений, выведем уравнение Эйринга для бимолекулярной реакции. Поскольку активированный комплекс находится как бы в процессе распада на отдельные фрагменты, одно из внутренних колебаний[1], как было указано выше, Эйринг принял за поступательное движение в сторону реакции. Предполагается, что это колебание имеет классическую энергию
В классической теории принято, что энергия равномерно распределяется по степеням свободы, т.е. на каждую степень свободы соотносят энергию равную (kT/2). Поскольку колебательное движение связано с изменением как потенциальной, так и кинетической энергии, то на одну колебательную степень свободы отводится в два раза большее значение энергии, т.е. kT.
В квантовой теории показано, что энергия молекулярного колебания равна hn. Следовательно
Частота колебательного движения n, согласно предположению Эйринга, принимается равной скорости, с которой активированный комплекс движется через потенциальный барьер. Следовательно, для реакции (12.40) скорость реакции - это есть скорость прохождения комплекса через барьер, умноженная на концентрацию активированного комплекса:
v=
В этом уравнении введен трансмиссионный коэффициент k, который представляет собой вероятность того, что молекула прошедшая через потенциальный барьер, продолжит свой путь вперед, а не возвратится назад. При расчетах обычно полагают k =1. Поскольку в теории Эйринга принимается, что активированные комплексы находятся в равновесии с исходными веществами, то для расчетов можно использовать методы термодинамики и статистической механики, а значит законом действующих масс:
и уравнением изотермы:
Подстановка в уравнение дает:
Откуда для константы скорости реакции второго порядка можно записать
Константу равновесия К++ выразим из уравнения изотермы (12.45):
DG++0 – представляет собой изотермическую работу, необходимую для медленного перехода конфигурации молекул реагентов, находящихся в стандартном в критическое состояние активированного комплекса, находящегося в стандартном состоянии. С другой стороны изменение стандартного изобарного потенциала в процессе активации связано с термодинамическими характеристиками предполагаемого равновесия уравнением Гиббса - Гельмгольца:
Поэтому уравнение (52) можно переписать как
Это и есть фундаментальное уравнение теории Эйринга. Хотя мы получили этот результат для константы скорости реакции второго порядка, он является совершенно общим. Более того, в теории термодинамики показано, что теория Эйринга включает в себя ТАС как частный случай. Из-за множителя Т в предэкспоненциальном множителе уравнения Эйринга энтальпия активации оказывается не равной энергии активации в уравнении Аррениуса Еар. Соотношение между ними можно получить, если найти выражение для тангенса угла наклона линии lnk - 1/T. Последовательно логарифмируя и дифференцируя уравнение Эйринга (53) найдем:
Энтропийный множитель exp(DS++0 /к) является в этой теории аналогом стерического фактора р в теории активных столкновений. Значение DS++0 может быть больше, равно или меньше нуля. Это объясняет возможность p> 1, что было необъяснимо в ТАС. По значению DS++0 реакции делятся на три группы. При DS++0 >>0 (р >1) реакции быстрые; при DS++0 = 0 (р =0) реакции нормальные; при DS++0 <<0 (р <1) реакции медленные. Доказательство в теории переходного состояния того факта, что реакции зависят не только от энергии активации, но и от энтропии активации, позволяет объяснить различие в скоростях реакций с близкими энергиями активации. Скорость будет больше там, энтропия активации больше.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.159.5 (0.009 с.) |

 (45)
(45) (46)
(46)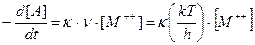 (47)
(47) (48)
(48) (47)
(47) (48)
(48) (49)
(49)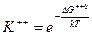 (50)
(50)
 (51)
(51) (52)
(52)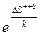
 (53)
(53) (54)
(54)


