
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цикл паровой компрессионной холодильной установкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Паровые компрессионные установки позволяют в области насыщенного пара приблизить холодильный цикл к обратному циклу Карно. Насыщенный пар низкокипящей жидкости (хладагента) всасывается компрессором и адиабатно сжимается до давления конденсации p2 с затратой работы lц (процесс 1-2). После компрессора сжатый пар поступает в конденсатор, где при постоянном давлении p2 вследствие отнятия у пара теплоты q1 охлаждающей водой (процесс 2-2’-3) снижается температура перегретого пара (2-2’), а затем при постоянной температуре насыщенного пара осуществляется полная конденсация (2’-3).
Для дальнейшего снижения температуры хладагента можно было бы применить расширительную машину и осуществлять в ней адиабатное расширение 3-4’ (с производством внешней работы за счет убыли внутренней энергии). Однако для упрощения установки и обеспечения гибкой регулировки расширительную машину заменяют регулирующим дроссельным вентилем, в котором хладагент после конденсатора дросселируется с понижением давления и температуры (процесс 3-4). На диаграмме T-s процесс дросселирования, как необратимый, условно показан пунктиром 3-4 (h=const). После дроссельного вентиля (точка 4) образовавшаяся парожидкостная смесь (влажный пар) с низкой температурой T2 поступает по трубам в испаритель, который находится в холодильной камере X. В испарителе при постоянных температуре T2 и давлении p1 происходит отбор теплоты q2 от охлаждаемых объектов (производство холода) и за счет этого испарение (кипение) хладагента (процесс 4-1). Образовавшийся пар (точка 1) вновь засасывается компрессором, и цикл повторяется. Холодильный коэффициент:
Количество теплоты q2, отнятой 1 кг хладагента от охлаждаемой среды, называется удельной хладопроизводительностью q2 = пл. |41ba4| = h1 – h4 = h1 – h3. Количество теплоты, переданной в конденсаторе охлаждающей среде при постоянном давлении: q1 = пл. |22’3’3b2| = h2 – h3. Тогда
Отсюда следует, что ε увеличивается с повышением температуры в испарителе T2, (чем выше расположена линия 4-1, тем больше хладопроизводительность) и понижением температуры охлаждающе среды в конденсаторе T1 (линия 2’-2 расположена ниже, затрачиваемая работа в компрессоре меньше). Затрата работы в компрессоре при адиабатном сжатии 1-2
что на диаграмме T-s соответствует пл. |122’34”1|. Эффективность холодильных установок зависит от свойств хладагентов, к которым предъявляется ряд требований: - давление насыщенного пара хладагента, соответсвующее требуемым низким температурам, должно быть выше атмосферного, так как при этом легче бороться с утечкой хладагента, чем с подсосом воздуха при вакууме; попадающий в хладагент воздух сильно ухудшает теплопередачу и содержит влагу, которая может замерзать при низкой температуре; - теплота парообразования r должна быть по возможности большей, так как при одном и том же расходе хладагента она определяет хладопроизводительность установки; - хладагенты не должны вредно воздействовать на здоровье человека и не должны обладать корродирующими свойствами Наиболее распространенным хладагентом является аммиак (tн = –33,5 ºС), позволяющий получить достаточно высокий холодильный коэффициент и относительно невысокое давление в цикле. Однако из-за токсичности аммиака в последнее время широко применяются фреоны (в частности, фреон-12). По термодинамическим свойствам фреон-12 ближе к аммиаку, хотя меньшая его теплота парообразования обусловливает большой расход хладагента.
ЛЕКЦИЯ 9 Основы теории теплообмена Теплопередача - это процесс переноса теплоты от одного теплоносителя к другому через разделяющую стенку. Теплопередача связана с весьма сложными процессами и при ее изучении необходимо знать законы теории теплообмена и методы анализа, применяемые в физике, термодинамике, гидродинамике и химии. Сложный процесс переноса теплоты разбивают на ряд более простых. Такой прием упрощает его изучение. Кроме того, каждый простой процесс переноса теплоты подчиняется своим законам. Существует три простейших способа передачи теплоты: теплопроводность, конвекция, излучение. Явление теплопроводности состоит в переносе теплоты микрочастицами (молекулами, атомами, электронами и т.п.). такой теплообмен может происходить в любых телах с неоднородным распределением температур. Конвективный теплоперенос (конвекция) наблюдается лишь в жидкостях и газах. Конвекция - это перенос теплоты вместе с макроскопическими объемами вещества. Следует иметь ввиду, что одновременно с конвекцией всегда существует и теплопроводность. Однако конвекция обычно является определяющей, т.к. она интенсивнее теплопроводности. Конвекцией можно передавать теплоту на очень большие расстояния (например, при движении газа по трубам). Движущаяся среда (жидкость или газ), используемая для переноса теплоты, называется теплоносителем. Третьим способом переноса теплоты является излучение. За счет излучения теплота передается во всех лучепрозрачных средах, в том числе и в вакууме. Носителями энергии при теплообмене излучением являются фотоны, излучаемые и поглощаемые телами, участвующими в теплообмене. В большинстве случаев перенос тепла осуществляется несколькими способами одновременно. Например, конвективная теплопередача от газа к стенке практически всегда сопровождается параллельным переносом теплоты излучением. Основные понятия и определения Интенсивность переноса теплоты характеризуется плотностью теплового потока. Плотность теплового потока - это количество теплоты, передаваемое в единицу времени через единичную плотность поверхности, q [Вт/м2]. Мощность теплового потока или просто тепловой поток - это количество теплоты, передаваемое в единицу времени через произвольную поверхность F, [Вт]. q=Q/F, Вт/м2 поверхность теплообмена F - это поверхность, через которую происходит передача тепла. Например, при остывании теплоносителя в трубе диаметром d и длиной l, тепло передается от горячего теплоносителя к окружающей среде через цилиндрическую поверхность трубы. В этом случае Перенос теплоты зависит от распределения температуры по объему тела или пространства. Температурным полем называется совокупность мгновенных значений температуры во всех точках тела или системы тел в данный момент времени. Математическое описание температурного поля имеет вид: t=f(x,y,z,t), где t - температура; x,y,z - пространственные координаты;
Температурное поле, описываемое приведенным уравнением, называется нестационарным. В этом случае температуры зависят от времени. В том случае, когда распределение температуры в теле не изменяется со временем, температурное поле называется стационарным t=f(x,y,z,), если температура изменяется только по одной или двум пространственным координатам, то температурное поле называется соответственно одно - и двухмерным: t=f(x,t), Температурные поля (1.2) и (1.3) называются трехмерными. Поверхность, во всех точках которой температура одинакова, называется изотермической. Изотермические поверхности могут быть замкнутыми, но не могут пересекаться. Быстрее всего температура изменяется при движении в направлении, перпендикулярном изотермической поверхности. Скорость изменения температуры по нормали к изотермической поверхности характеризуется градиентом температуры.
 , ,
где
Теория теплопроводности Закон Фурье Теория теплопроводности рассматривает тело как непрерывную среду. Согласно основному закону теплопроводности - закону Фурье - вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален вектору градиента температуры:
где Знак «-» указывает на противоположное направление вектора теплового потока и вектора градиента температуры. Вектор плотности теплового потока q всегда направлен в сторону наибольшего уменьшения температуры. скалярная величина вектора плотности теплового потока:
Из формулы следует, что коэффициент теплопроводности коэффициент теплопроводности является физическим параметром и зависит от химической природы вещества и его физического состояния (плотности, влажности, давления, температуры). Диапазоны изменения
Рисунок 9.2 - Теплопроводность при стационарном режиме
       Рассмотрим однородную плоскую стенку толщиной d, на поверхностях которой поддерживаются температуры tс1 и tс2, причем tс1>tс2 (рис.2.2). температура изменяется только по толщине стенки - по одной координате х, коэффициент теплопроводности Рассмотрим однородную плоскую стенку толщиной d, на поверхностях которой поддерживаются температуры tс1 и tс2, причем tс1>tс2 (рис.2.2). температура изменяется только по толщине стенки - по одной координате х, коэффициент теплопроводности  . Теплового потока в этом случае, в соответствии с законом Фурье, определяется по формуле: . Теплового потока в этом случае, в соответствии с законом Фурье, определяется по формуле:
или
где
Распределение температур в плоской однородной стенке - линейное. В большинстве практических задач приближенно предполагается, что коэффициент теплопроводности Тепловой поток (мощность теплового потока) определяется по формуле:
Многослойная плоская стенка
       
  
 
   
В этом случае плотность теплового потока определяется по формуле:
 , ,
где n - число слоев многослойной стенки; tc1 и tc(n+1) - температуры на внешних границах многослойной стенки;
Плотность теплового потока, проходящего через все слои, в стационарном режиме одинакова. А так как коэффициент теплопроводности l различен, то для плоской многослойной стенки распределение температур - ломанная линия. Рассчитав тепловой поток через многослойную стенку, можно найти температуру на границе любого слоя. Для к-го слоя можно записать:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.008 с.) |


 .
. .
.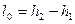 ,
, .
. - время.
- время.

 -единичный вектор, направленный в сторону возрастания температур нормально к изотермической поверхности.
-единичный вектор, направленный в сторону возрастания температур нормально к изотермической поверхности. ,
, - коэффициент теплопроводности, Вт/(м×К). Он характеризует способность вещества, из которого состоит рассматриваемое тело, проводить теплоту.
- коэффициент теплопроводности, Вт/(м×К). Он характеризует способность вещества, из которого состоит рассматриваемое тело, проводить теплоту. ,
, определяет плотность теплового потока при градиенте температуры 1 К/м.
определяет плотность теплового потока при градиенте температуры 1 К/м.
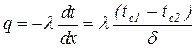 ,
, ,
, , причем tс1>tс2;
, причем tс1>tс2; - внутреннее термическое сопротивление теплопроводности стенки, (м2×К)/Вт.
- внутреннее термическое сопротивление теплопроводности стенки, (м2×К)/Вт. .
. ,
, - полное термическое сопротивление многослойной плоской стенки.
- полное термическое сопротивление многослойной плоской стенки. ,
,


