Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет закрытой конической передачи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
3.1. Выбор материала колес зубчатой передачи. Сталь в настоящее время – основной материал для изготовления зубчатых колес и червяков. Одним из условий совершенствования редукторостроения является повышение контактной прочности активных поверхностей зубьев и их прочности на изгиб. При этом снижается масса и габаритные размеры зубчатой (червячной) передачи, а это повышает ее технический уровень. В условиях индустриального и мелкосерийного производства, предусмотренного техническими заданиями на курсовое проектирование, в мало- и средненагруженных передачах, а также в открытых передачах с большими колесами применяются зубчатые колеса (червяки) с твердостью материала Н≤350 НВ. При этом обеспечивается чистовое нарезание зубьев после термообработки, высокая точность в изготовлении и хорошая прирабатываемость зубьев. Материал для шестерни и колеса выбираем по таблице 3.1 [ист. _ стр. 52], при условии, что данная передача выполнена с круговым зубом, что способствует уменьшению уровня шума при работе редуктора, а так же обеспечивает более высокую плавность хода. Шестерня: Сталь 35ХМ 262…302 НВ Колесо: Сталь 40ХН 235…269 НВ Термообработка для шестерни улучшение + закалка ТВЧ. Термообработка для колеса - улучшение. 2. Определяем коэффициенты долговечности:
Где
Определяем коэффициент долговечности шестерни:
Определяем коэффициент долговечности колеса:
3. Определяем допускаемые контактные напряжения:
Шестерня:
Колесо:
4. Определяем допускаемое напряжение изгиба:
Шестерня:
Колесо:
3.2. Проектный расчет.
Проектный расчет выполняется по допускаемым контактным напряжениям с целью определения геометрических параметров редукторной пары. 1. Определяем главный параметр передачи – внешний делительный диаметр колеса:
КНβ = 1,1 – коэффициент, учитывающий распределение нагрузки по ширине зубчатого венца. ӨН = 1,85 – коэффициент вида конических колес. Тогда
Полученное значение округляем до стандартной длины по таблице 13.15 [ист. 4 стр. 326].
2. Определяем углы делительных конусов шестерни и колеса:
3. Определяем внешнее конусное расстояние:
4. Определяем ширину венца шестерни и колеса:
ψR = 0,285 – коэффициент ширины венца колеса:
Округляем до стандартного значения по таблице 13.15 [ист. 4 стр. 326] по Ra 20.
5. Определяем внешний окружной модуль зубчатой передачи:
КFβ = 1,08 – коэффициент, учитывающий распределение нагрузки по ширине зубчатого венца. θF = 1 – коэффициент вида конических колес. Тогда
Принимаем 6. Определяем число зубьев колеса и шестерни:
7. Определяем фактическое передаточное отношение и проверяем его отклонение:
8. Определяем действительные углы конусов шестерни и колеса:
9. По таблице 4.6 [ист. 4 стр.71] определяем коэффициенты смещения:
10. Определяем фактические внешние диаметры шестерни и колеса: Делительный диаметр:
Диаметр вершин зубьев:
Диаметр впадин зубьев:
11. Определяем средний делительный диаметр шестерни и колеса:
3.3. Проверочный расчет.
Проверочный расчет должен подтвердить правильность выбора табличных величин, коэффициентов и полученных результатов в проектном расчете, а также определить соотношения между расчетными и допускаемыми напряжениями изгибной и контактной выносливости. При неудовлетворительных результатах проверочного расчета нужно изменить параметры передачи и повторить проверку. 1. Проверяем контактные напряжения:
Окружная сила в зацеплении:
КНα = 1 – коэффициент, учитывающий распределение нагрузки между зубьями. КНυ = 1,08 – коэффициент динамической нагрузки. Определяется по таблице 4.3 [ист. 4 стр. 64…65] при v = 0,5ω3d2 = 1,3 м/с и 8-ом классе точности. Тогда
Передача удовлетворяет условиям контактной прочности. 2. Проверяем напряжение изгиба зубьев колеса:
КFα = 1 – коэффициент, учитывающий распределение нагрузки между зубьями. КFυ = 1,07 – коэффициент динамической нагрузки. Определяется по таблице 4.3 [ист. 4 стр. 64…65] при v = 1,3 м/с и 8-ом классе точности. YF2 – коэффициент формы зуба колеса. Определяется по таблице 4.7 [ист. 4 стр. 71] в зависимости от эквивалентного числа зубьев колеса.
β =35° – угол наклона зубьев.
Yβ = 1 – коэффициент учитывающий наклон зуба. Тогда:
3. Проверяем напряжение изгиба зубьев шестерни:
YF1 – коэффициент формы зуба шестерни. Определяется по таблице 4.7 [ист. 4 стр. 71] в зависимости от эквивалентного числа зубьев шестерни.
Тогда:
Полученные при расчете данные заносим в таблицу.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 781; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.008 с.) |

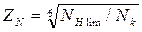 при
при 
 при
при 

 закладываемый при проектировании рабочий ресурс привода.
закладываемый при проектировании рабочий ресурс привода.
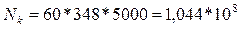

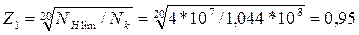

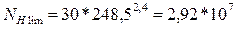



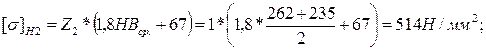



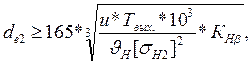 где
где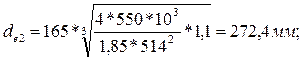

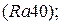


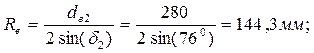
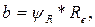 где
где

 где
где



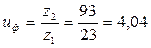











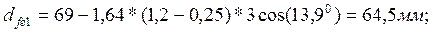



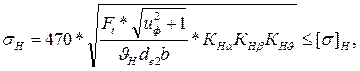 где
где

 где
где где
где
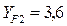

 где
где