
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические свойства дисперсииСодержание книги
Поиск на нашем сайте 1.Дисперсия постоянной величины равна нулю 2.Если величину признака уменьшить на постоянную величину А, то величина дисперсии не изменится
3.Если все значения варианта уменьшить в k раз, то значение дисперсии уменьшится в
Расчет дисперсии упрощенным способом Для расчета дисперсии упрощенным способом используют её свойства. При этом последовательно выполняется ряд шагов: 1. Выбирается условный нуль – вариант, находящийся в середине ряда распределения или вариант с наибольшей частотой. 2. Все значения признака уменьшаются на величину А – условный нуль, т.е. находится отклонение вариантов признака от условного нуля. 3. Все отклонения значений от условного нуля уменьшаются в k раз, часто за k принимают величину интервала или значение, кратное величине отклонения. В результате этих действий получают ряд распределения от условной величины 4.Исчисляют условную среднюю 5.Исчисляют среднюю из квадратов условных величин
6.Исчисляется условная дисперсия.
7.Исчисляется дисперсия от величины х:
Пример:
Дисперсия альтернативного признака Наряду с количественной вариацией признака может иметь место качественная вариация. Если имеют место два взаимоисключающих друг друга признака, то вариация называется альтернативной. Вариация альтернативного признака выражается в том, что одни единицы обладают данным признаком, а другие нет. Наличие признака у единицы совокупности обозначается 1, а его отсутствие – 0, долю единиц, обладающих данным признаком, обозначают p, а не обладающих данным признаком – q. Рассчитаем дисперсию альтернативного признака:
Если распределение альтернативного признака в совокупности неизвестно, то принимают p=q =0,5. В этом случае дисперсия альтернативного признака принимает максимальное значение, равное 0,25. Пример: В результате экзамена 90% студентов получили “удовлетворительно”, остальные – “неудовлетворительно”. Определить дисперсию альтернативного признака.
Тема 7. Статистическое изучение взаимосвязи социально – экономических явлений 1. Характеристика статистической связи 2. Формально статистические методы изучения связи. 3. Корреляционно – регрессионный метод изучения связи Парная корреляция Логический смысл параметров уравнения линейной регрессии Множественная корреляция 4. Показатели тесноты связи Параметрические показатели тесноты связи Непараметрические показатели тесноты связи (эмпирические меры тесноты связи) Характеристика статистической связи Изучение взаимосвязи – важнейшая познавательная задача статистики. Её решение начинается с выяснения социально – экономической сущности явлений. Явления и процессы природы и общества органически связаны между собой. Зависят друг от друга, взаимообуславливают друг друга. Статистический анализ позволяет установить причинно – следственное отношение между явлениями и выявить признаки, Факторы, оказывающие решающее воздействие на вариацию изучаемого явления. Статистические методы изучения взаимосвязи между социально – экономическими явлениями и признаками позволяют: ` Выявить наличие и направление связи ` Измерять её количественно ` Выразить связь аналитически Статистика разработала методы, дающие возможность изучения не только простых парных связей между двумя явлениями или признаками, но и множественных связей между многими явлениями и признаками. Связи между признаками принято характеризовать по ряду оснований: 1. По роли признака во взаимосвязи c Факторные признаки, оказывающие воздействие на вариацию изучаемого явления. c Результативные признаки, меняющиеся под воздействием факторного.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |


 раз.
раз.
 ,равной
,равной 

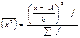





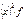






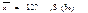

 ,где p+q=1
,где p+q=1




