
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики центра розподілу.Содержание книги
Поиск на нашем сайте
Характеристиками центру розподілу в будь-якому ряді розподілу є:
Характеристики варіації В статистичних сукупностях індивідуальні значення ознаки, тобто варіанти ряду розподілу, можуть або певним чином відхилятися від центру розподілу або, щільно групуватися навколо нього. Чим менше відхилення, тим одно ріднішою буде статистична сукупність, а отже, тим більш надійними і типовими будуть характеристики рядів розподілу. Вимірювання ступеня коливання індивідуальних значень ознаки від центру розподілу є невід'ємною складовою аналізу закономірностей розподілу. Ступінь відхилення значень від центру розподілу називають варіацією. Для вимірювання та оцінювання варіації використовують показники варіації – показники, які визначають міру коливання значень ознаки від центру розподілу. Показники варіації поділяють на: 1. Абсолютні – визначають межі, в яких змінюється значення ознаки та різноманітні відхилення індивідуальних значень ознаки від центру розподілу. 2. Відносні – характеризують співвідношення абсолютних характеристик варіації і центру розподілу та використовуються при порівнянні варіації різних ознак однієї сукупності та однієї ознаки в різних сукупностях. Показники варіації
Характеристики форм розподілу. Різноманітність
Тема № Статистичне вивчення динаміки Зміст 1 Поняття про ряди динаміки. Види та правила побудови. 2 Аналітичні показники рядів динаміки. 3 Середні показники рядів динаміки. 4 Основні прийоми аналізу рядів динаміки. 5 Вимірювання сезонних коливань.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.98.91 (0.008 с.) |




 і значення варіанти, яке відповідає цій частоті і буде модою
і значення варіанти, яке відповідає цій частоті і буде модою 


 . Серед всіх кумулятивних частот знаходять таку, яка не менша за половину обсягу сукупності тобто таку, що
. Серед всіх кумулятивних частот знаходять таку, яка не менша за половину обсягу сукупності тобто таку, що  .
.
 Варіанта, яка відповідатиме їй і буде медіаною.
Варіанта, яка відповідатиме їй і буде медіаною.





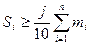 .
.
 Варіанта, яка відповідатиме їй і буде відповідним децилем.
Варіанта, яка відповідатиме їй і буде відповідним децилем.






