
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сформулируйте теорему о замене переменной в неопределенном интеграле и Правило интегрирования по частям. Докажите любое из этих двух утверждений.Содержание книги
Поиск на нашем сайте
Замена переменной Теорема: Пусть ф-я x = j(t) определена и диф-ема на промежутке Т и Х – мн-во ее зн-й, на кот определена ф-я f(x). Тогда если F(x) – первообразная f(x) на Х, то F(j(t)) - первооб для f(j(t)) j¢(t) на Т, т.е. на множестве Т выполняется ра-во Док-во: По правилу диф-ия сложной ф-и производная левой части равенства равна:
Что совпадает с подынтегр ф-ей в правой части рав-ва, это и док-ет рав-во. Т-ма док-на. Пример. Найти неопределенный интеграл Сделаем замену t = sinx, dt = cosxdt.
Интегрирование по частям. Пусть u(x) и v(x) – две дифференцируемые функции на промежутке Х. Тогда на Х выполняется формула интегрирования по частям: Док-во Имеем фор-лу для диф-ла произведения ф-й uv: d(uv) = udv + vdu Проинт-в обе части рав-ва, получаем: Получили фор-у инте-ия по частям, кот позв-ет нах-ть инт-лы мн-их элем ф-й. Пример: 43. Дайте определение и приведите пример первообразной. Сформулируйте теорему о существовании первообразной для непрерывной функции. 1.Функция F(x) называется первообразной для функции f(x) на промежутке ХÌR, если для любого Пример: Непрерывная ф-ция F(x)=sinx - первообразная функции y=cosx на x=(-¥;+¥), F’(x)=(sinx)'=cosx 2. Теорема. Если y=f(x) непрерывна на xÌR, то у нее на х существует первообразная F(x). Если F(x) первообр ф-и f(x) на xÌR, то G(x)=F(x)+C(общий вид первообр на х ф-и f(x) Пример: см. выше 44. Дайте определение определенного интеграла и приведите формулу Ньютона-Лейбница. Сформулируйте основные свойства определенно го интеграла, иллюстрируя их примерами. Пусть функция
Рассмотрим интегральные суммы, соответствующие разбиениям отрезка 2. Формула Ньютона – Лейбница: Пусть ф-ция y=f(x) непрерывна на отрезке [a,b] и F(x) – первообразная для f(x). Тогда Пример. 3. Основные св-ва определенного интеграла: 1. Пример. 2. 3.
4.
5.если f(x)£g(x) на отрезке [a,b], то 6.если на отрезке [a,b] выполняется m£f(x)£M,то m(b-a)£ пример. M=3/5,m=1/2 на [0;2] c помощью производной ½(2-0)£ 7.теорема о среднем Для непрерывной на отрезке[a,b] функции y=f(x) найдется точка сÎ[a,b]
45. Напишите формулы вычисление площади криволинейной трапеции и объема тела вращения. Приведите в обоснование чертежи к каждой из формул и приведите примеры. Вычисление площадей плоских фигур.
Изв-но, что опред-ый инт на отрезке предст-ет собой площадь криволин трапеции, огран-ой гр-ом ф-и f(x). Если гр расположен ниже оси Ох, т.е. f(x) < 0 (случай 2), то площадь имеет знак “-“, если гр расп выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+” (случай 1). Для нахождения суммарной площади используется формула Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий. Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
Объем тел вращения. Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что ф-я f(x) непр-на на отре [a, b]. Если соотвую ей кривол трапецию с основаниями а и b вращать вокруг оси Ох, то получим так наз-ое тело вращения.
При вращении вокруг оси Оу рассуждения аналогичны, только Пример: Вычислить объем тела вращения, образованного вращением вокруг оси абсцисс фигуры, ограниченной гиперболой
46. Дайте определения несобственных интегралов с бесконечными пределами. Приведите примеры вычисления таких интегралов. Пусть ф-я f(x) опр-на и непр-на на инт-ле [a, ¥). Тогда она непр-на на любом отрезке [a, b]. Оп-е: Если существует конечный предел Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится. Если предел не существует или бесконечен, то несобственный интеграл расходится. Аналогичные рассуждения можно привести для несобственных интегралов вида:
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют. Пример. Несобственный интеграл расходится. Пример. 47. Дайте определение двойного интеграла. Сформулируйте определение элементарной области вдоль координатной оси и правило вычисления двойного интеграла. Приведите пример вычисления двойного интеграла. Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой f(x, y) = 0. Разобьем область D на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние Dхi, а по оси у – на Dуi. Вообще говоря, такой порядок разбиения наобязателен, возможно разбиение области на частичные участки произвольной формы и размера.Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны Si = Dxi × Dyi. В каждой частичной области возьмем произвольную точку Р(хi, yi) и составим интегральную сумму
где f – ф-я непр-ая и однозначная для всех точек области D. Если беск увел-ть кол-во частичных обл-ей Di, тогда, очевидно, площадь каж частичного участка Si стремится к нулю. Опр-е: Если при стремлении к нулю шага разбиения обл D интегральные суммы
С учетом того, что Si = Dxi × Dyi получаем:
В прив-ой выше записи им-ся два знака S, т.к. сумм-ние производится по 2 перем х и у. Т.к. деление области интегрирования произвольно, также произволен и выбор точек Рi, то, считая все площади Si одинаковыми, получаем формулу:
Теорема. Если ф-я f(x, y) непр-на в замкнутой обл D, огран-ой линиями х = a, x = b, (a < b), y = j(x), y = y(x), где j и y - непрерывные функции и j £ y, тогда
Пример. Вычислить интеграл
48. Сформулируйте определения числового ряда и его суммы. В чем состоит достаточный признак сходимости ряда. Гармонический ряд. Числовой ряд. Пусть дана {un}- числ. послед.; Числовым рядом называется бесконечная сумма членов послед. un т.е. u1+u2+…+un+… обозначение: Ряд
Критерий Коши (необ-ые и дост усл-я сходимости ряда): Для того, чтобы посл-ть Для того, чтобы ряд В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда: . 49. Сформулируйте определения и приведите признаки сходимости положительных и знакочередующихся рядов. Проиллюстрируйте это на примерах. Положительный ряд можно записать в виде: Предельный признак Даламбера является сле-ем из приведенного выше признака Даламбера. Если существует предел Пример. Определить сходимость ряда
Признак Коши. (радикальный признак) Если для ряда то ряд
Следствие. Если сущ-ет предел Пример. Определить сходимость ряда
Т.е. признак Коши не дает ответа на вопрос о сх-ти ряда. Проверим вып-е необ-ых условий сх-ти. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.
Интегральный признак Коши. Если j (х) – непрерывная положительная функция, убывающая на промежутке [1;¥), то ряд j (1) + j (2) + …+ j (n) + … = Пример. Ряд Знакочередующийся ряд можно записать в виде:
Признак Лейбница. Если у знакочередующегося ряда Примером условно сходящегося знакочередующегося ряда может служить ряд:
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.42.25 (0.006 с.) |



 .
.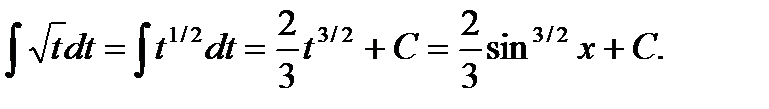

 , а в соотв-и с прив-ми выше св-ми неопр-го интеграла:
, а в соотв-и с прив-ми выше св-ми неопр-го интеграла:  или
или  ;
;
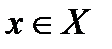 функция y=F(x) дифференцируема и выполняется равенство
функция y=F(x) дифференцируема и выполняется равенство 
 определена на отрезке
определена на отрезке 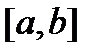 . Разобьем отрезок на
. Разобьем отрезок на  частей точками
частей точками  (
( ) такими, что
) такими, что  . Длины полученных отрезков обозначим
. Длины полученных отрезков обозначим  (
( ), и пусть
), и пусть  – наибольшая из этих длин. Выберем на каждом из отрезков разбиения произвольную точку
– наибольшая из этих длин. Выберем на каждом из отрезков разбиения произвольную точку  и составим сумму
и составим сумму , которую назовем интегральной суммой для функции
, которую назовем интегральной суммой для функции  .
. . Если существует предел таких сумм при
. Если существует предел таких сумм при 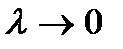 , то он называется определенным интегралом функции
, то он называется определенным интегралом функции  на отрезке
на отрезке  ,
,

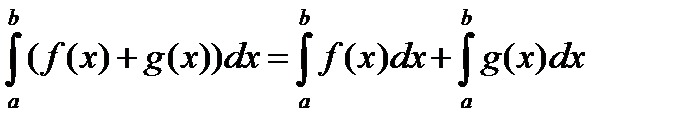

 , где k – постоянная.Пример.
, где k – постоянная.Пример.  =1
=1
 =0;
=0; 
 Пример.
Пример. 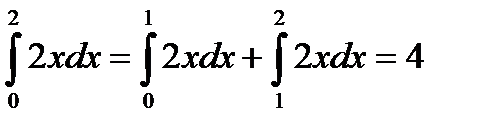
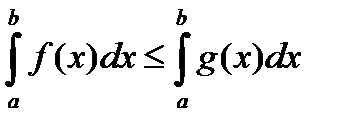
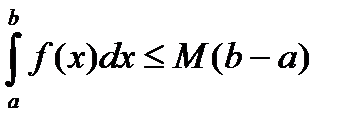 (оценка интеграла)
(оценка интеграла)
 £3/5(2-0)
£3/5(2-0)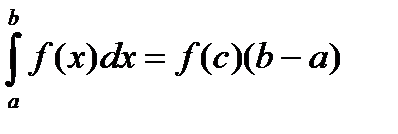



 .В 3 случае имеем область, принадлежащую обеим криволинейным трапециям (как для верхней, так и для нижней функции). В данном случае площадь заштрихованной области – разница площадей трапеций верхнего и нижнего графиков функций.
.В 3 случае имеем область, принадлежащую обеим криволинейным трапециям (как для верхней, так и для нижней функции). В данном случае площадь заштрихованной области – разница площадей трапеций верхнего и нижнего графиков функций. 
 Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
Искомая площадь (заштрихована на рисунке) может быть найдена по формуле: (ед2)
(ед2) Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса
Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса 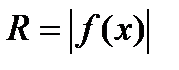 , то объем тела вращения может быть легко найден по полученной выше формуле:
, то объем тела вращения может быть легко найден по полученной выше формуле: 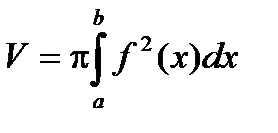
 Примечание: Рисунок тот же только вместо х написать у.
Примечание: Рисунок тот же только вместо х написать у.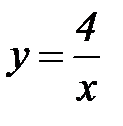 , осью абсцисс и прямыми
, осью абсцисс и прямыми 


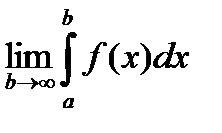 , то этот предел называется несоб-м интегралом от ф-и f(x) на интервале [a, ¥). Обозначение:
, то этот предел называется несоб-м интегралом от ф-и f(x) на интервале [a, ¥). Обозначение: 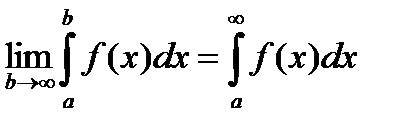


 - не существует.
- не существует. - интеграл сходится
- интеграл сходится Сово-ть всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой обл-ю D. Если выбрать точки обл-и без учета точек, лежащих на кривой, область будет называется незамкнутой область D.С геом точки зрения D - площадь фигуры, огран0ой контуром.
Сово-ть всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой обл-ю D. Если выбрать точки обл-и без учета точек, лежащих на кривой, область будет называется незамкнутой область D.С геом точки зрения D - площадь фигуры, огран0ой контуром.
 имеют кон предел, то этот пр наз-ся двойным инт-ом от ф-и f(x, y) по обл D.
имеют кон предел, то этот пр наз-ся двойным инт-ом от ф-и f(x, y) по обл D.
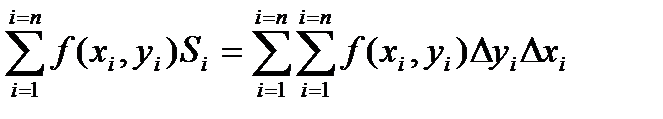



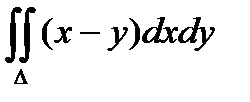 , если область D ограничена линиями: y = 0, y = x2, x = 2.
, если область D ограничена линиями: y = 0, y = x2, x = 2.
 =
= 

 называется сходящимся, если сходится посл-ть его частных сумм к некот числу S. S-сумма ряда. Сумма сход ряда – предел посл-ти его частных сумм.
называется сходящимся, если сходится посл-ть его частных сумм к некот числу S. S-сумма ряда. Сумма сход ряда – предел посл-ти его частных сумм.
 была сходящейся, необ-мо и дост-но, чтобы для любого
была сходящейся, необ-мо и дост-но, чтобы для любого  сущ-вал такой номер N, что при n > N и любом p > 0, где р – целое число, вып-ось бы нерав-во:
сущ-вал такой номер N, что при n > N и любом p > 0, где р – целое число, вып-ось бы нерав-во:  .
. был сход-ся необ-мо и дост-но, чтобы для любого существовал номер N такой, что при n>N и любом p>0 вып-ось бы нер-о
был сход-ся необ-мо и дост-но, чтобы для любого существовал номер N такой, что при n>N и любом p>0 вып-ось бы нер-о 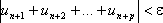
 Ряд назван гармоническим так как каждый его член, начиная со второго, является гармоническим средним двух соседних. Согласно интегральному признаку, ряд расходится!
Ряд назван гармоническим так как каждый его член, начиная со второго, является гармоническим средним двух соседних. Согласно интегральному признаку, ряд расходится!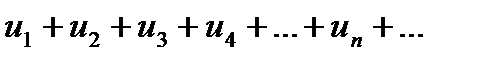 где
где 
 , то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то на вопрос о сходимости ответить нельзя.
, то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то на вопрос о сходимости ответить нельзя.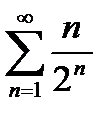 .
. Вывод: ряд сходится.
Вывод: ряд сходится. с неотриц-ми членами сущ-ет такое число q<1, что для всех достаточно больших n вып-ся нер-во
с неотриц-ми членами сущ-ет такое число q<1, что для всех достаточно больших n вып-ся нер-во 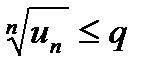 ,
, то ряд
то ряд  , то при r<1 ряд сх-ся, а при r>1 ряд расходится.
, то при r<1 ряд сх-ся, а при r>1 ряд расходится. .
.
 , т о, необ-ое усл-е сх-ти не выполняется, значит, ряд расходится.
, т о, необ-ое усл-е сх-ти не выполняется, значит, ряд расходится. и несобственный интеграл
и несобственный интеграл  одинаковы в смысле сходимости.
одинаковы в смысле сходимости. сх-ся при a>1 и расх-ся a£1 т.к. соответствующий несобс интеграл
сх-ся при a>1 и расх-ся a£1 т.к. соответствующий несобс интеграл  сх-ся при a>1 и расх-ся a£1. Ряд
сх-ся при a>1 и расх-ся a£1. Ряд  наз-ся общегармоническим рядом.
наз-ся общегармоническим рядом.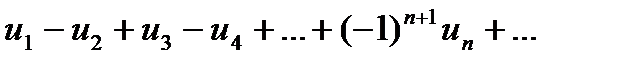 где
где  и общий член стремится к нулю
и общий член стремится к нулю  , то ряд сходится.
, то ряд сходится.



