
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сформулируйте правило Лопиталя. Докажите первый и второй замечательные пределы с помощью правила Лопиталя.Содержание книги
Поиск на нашем сайте Вначале отметим, что к разряду неопределенностей принято относить следующие соотношения: Теорема (правило Лопиталя). Если ф-и f(x) и g(x) дифф-емы в вблизи точки а, непр-ны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отн-ия ф-й при х®а равен пределу отн-я их производных, если этот предел (кон-й или беск-й) сущ-ет. Первый предел. Второй замечательный предел. Доказательство (правило Лопиталя и свойство
29. Дайте определения возрастающей и убывающей функций. В чем состоит необходимое и достаточное условия локального экстремума функции. Теорема (возрастание и убывание на отрезке): 1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f¢(x) ³ 0. 2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f¢(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b]. Анал-но можно сделать вывод о том, что если ф-я f(x) убывает на отрезке [ a, b ], то f¢(x) £0 на этом отрезке. Если f¢(x) <0 в пром-ке (a, b), то f(x) убыв на отрезке [ a, b ]. Конечно, данное утверждение справедливо, если ф-я f(x) непрерывна на отрезке [ a, b ] и дифференцируема на интервале (a, b). Рассмотрим функцию f (x) на множестве М⊆D(f). Число f (b) назовем наим-им значением ф-и f на мн-ве М (абсолютным или глобальным мин-ом) и обозначим f (b)=min x ∈ Mf (x), если точка b ∈М и f (x)≥ f (b) при любыx x ∈ M. 30. Дайте определения выпуклых вниз и вверх функций одного аргумента. Приведите достаточные условия выпуклости функции. Приведите примеры. Функция y=f(x) называется выпуклой вверх (вниз) на промежутке х Î R, если для любых x1 x2 и x3 этого промежутка выполняется:
Пример: Функция у = -х2 выпукла вверх на промежутке
у = -х2 , y¢ = -2x, y¢¢ = -2 у = х2 , y¢ = 2x, y¢¢ = 2 Т-ма 1 Ф-я y=f(x) вып вверх (вниз) на числ пром-ке X, если f¢¢(x) >0 (соотв-но <0) для всех х Î X. 31. В чем состоит необх и дост признаки точки перегиба графика функции. Приведите пример. Определение: Точкой перегиба непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх. Теорема 1. (необходимое условие перегиба). Вторая производная f¢¢(x) дважды дифференцируемой функции в точке перегиба х0 равна 0, т.е. f¢¢(x) = 0 Теорема 2.(достаточное условие перегиба). Если вторая производная f¢¢(x) дважды дифференцируемой функции при переходе через некоторую точку х0, меняет свой знак, то х0 есть точка перегиба её графика. Пример: Найдём точки перегиба графика функции y = (x)3 1.) y¢ = 3x2 2.) y¢¢ = 6x 6x=0, y¢¢ = 0, x0 =0 есть точкa перегиба гр ф-и. При переходе через данную точку ф-я действительно меняет свой знак (что видно из гр данной ф-и).
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 2086; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |


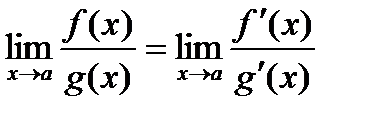
 Док-во (правило Лопиталя):
Док-во (правило Лопиталя): 
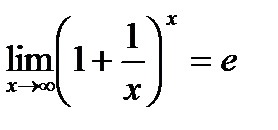
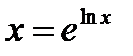 ):
): 
 , ч.т.д.
, ч.т.д.
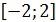 , т.к.
, т.к.
 0 Þ выпукла вверх
0 Þ выпукла вверх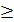 0 Þ выпукла вниз
0 Þ выпукла вниз


