
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сформулируйте с обоснованием ответ на вопрос: В чем состоит связь между дифференцируемостью и непрерывностью функции?Содержание книги
Поиск на нашем сайте
Рассмотрим следующие вопросы, который касаются функций: а) Если функция непрерывна, то она дифференцируема? б) Если функция дифференцируема, то она непрерывна? Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость. Ответ на второй вопрос: из дифференцируемости ф-и следует ее непрерывность. Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необ-мо док-ть озвученый факт или привести пример, кот опровергает этот факт. Найдем производную следующей функции
Покажем, что в точке нуль производная не существует. Для этого найдем производную в нуле по определению производной:
23. Обоснуйте возможность использования дифференциала в приближенных вычислениях. Приведите пример. Дифференциалом функции называется величина dy= f ′ (х)dх Рассмотрим подробнее формулу ∆y»dy или f ′ (х0+∆х) – f(х)» f ′ (х) ∆х; т.е. f ′ (х0+∆х)» f ′ (х0) ∆х + f ′(х0) – расчётная формула Эйлера; Найдём Полагаем y = f(x) =
2 способ Дифференциалом функции в точке х0 называется линейная относительно приращения аргумента часть приращения функции в этой точке, эквивалентная всему приращению. df(х0)= f ′ (х0) ∆х; ∆х=dх; df(х0)= f ′ (х0)dх
24. Сфор-те теоремы Лагранжа и Коши для дифференцируемых ф-й. Проверьте справедливость теоремы Лагранжа для функции Теорема Коши: Пусть ф-ции Домножим левую часть уравнения на Получили т-му Лагранжа. Теорема Лагранжа – это частный случай т. Коши, когда Теорема Лагранжа: Пусть функция Следствие 1: Если производная y¢=f¢(x) равна 0 на X, то для всех x Î Х выполняется f=const. Следствие 2: Правило Лопиталя 0:
Проверьте справедливость теоремы Лагранжа для функции f (х) =1 - y=1-(x4)1/5 ; f(-2) = 1-(-24)1/5 = f(2) В итоге: f ’(c)=0 Найдём f ’(x)=(1-(x4)1/5)’ = -4/5 *x-1/5=-4 / 5*x1/5 ¹ 0 Следовательно теорема Лагранжа не выполняется. 25. Сформ теоремы Лагранжа и Коши для дифференцируемых ф-й. Проверьте справедливость теоремы Лагранжа для функции Теорема Коши: Пусть ф-ции Домножим левую часть уравнения на Получили теорему Лагранжа. Теорема Лагранжа – это частный случай т. Коши, когда Теорема Лагранжа: Пусть функция Пример: y = f(x) =1/x на [-2; 2] 1. функция не является непрерывной на отрезке [-2; 2] Следовательно теорема Лагранжа не выполняется. 26. Сформулируйте теоремы Ферма и Ролля для дифференцируемых функций. Покажите, что функция Теорема (Ферма). Пусть f(x) определена и дифференцируема на некотором интервале (a;b) и в точке c Теорема (Ролля). Если ф-я f(x) непр-на на отрезке [a, b], дифф-ема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка с, a < с < b, в которой производная функция f(x) равная нулю, т.е. f¢(с) = 0. Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка с такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки. Парабола Сформулируйте теоремы Ферма и Ролля для дифференцируемых функций. Проверьте справедливость теорема Ролля для функции Пример: Значит в заданном интервале существует по крайней мере одна точка с, в которой производная функции обращается в нуль:
27. Сформ теоремы Ферма и Ролля для дифференцируемых функций. Проверьте справедливость теорема Ролля для функции Пример: Функция
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.137.13 (0.006 с.) |

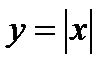 . Хорошо известно, что данная функция является непрерывной и что ее производная будет следующей:
. Хорошо известно, что данная функция является непрерывной и что ее производная будет следующей:
 Данный предел равен 1, если ∆ х →0+ и равен (–1), если ∆ х →0–, получается что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема.
Данный предел равен 1, если ∆ х →0+ и равен (–1), если ∆ х →0–, получается что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема.
 ; х0 = 1, ∆х = 0,01 и y¢ = f ′ (х) =
; х0 = 1, ∆х = 0,01 и y¢ = f ′ (х) =  , согласно расчётной формуле:
, согласно расчётной формуле: »
»  +
+ 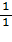 * 0,01» 0,01
* 0,01» 0,01

 на отрезке
на отрезке 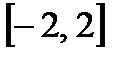 .
.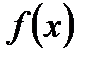 и
и  непрерывны на отрезке [a;b], дифференцируемы на интервале (a;b) и
непрерывны на отрезке [a;b], дифференцируемы на интервале (a;b) и 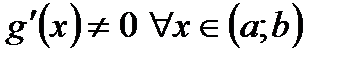 , тогда существует точка
, тогда существует точка  такая, что
такая, что 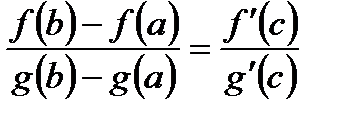 .
.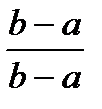
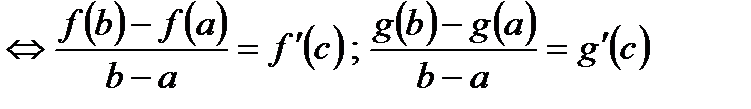
 .
. .
.
 4 на отрезке
4 на отрезке 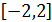 :
: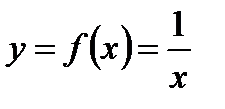 на отрезке
на отрезке 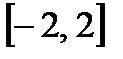 .
. удовлетворяет условиям теоремы Ферма на
удовлетворяет условиям теоремы Ферма на  и найдите соответствующее значение х = с на
и найдите соответствующее значение х = с на  .
. (a;b) принимает наибольшее (наименьшее) значение. Тогда
(a;b) принимает наибольшее (наименьшее) значение. Тогда  .
. определена и дифференцируема на заданном участке, а также имеет максимум в своей вершине (y max=4).
определена и дифференцируема на заданном участке, а также имеет максимум в своей вершине (y max=4).  , откуда, согласно теореме, х =1.
, откуда, согласно теореме, х =1. на отрезке
на отрезке 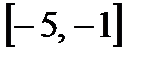 .
.
 .
.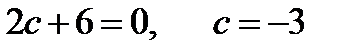 Причем
Причем  . Все условия теоремы Ролля выполнены.
. Все условия теоремы Ролля выполнены. на отрезке
на отрезке  .
. на концах отрезка [0, 8] принимает равные значения
на концах отрезка [0, 8] принимает равные значения  .
.  . При
. При  ,
, 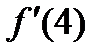 не существует. Нарушено условие теоремы Ролля.
не существует. Нарушено условие теоремы Ролля.


