
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дайте опр-я производной по напр-ю и градиента ф-и двух перем. ВчемСостоитОсновное св-о градиента ф-и.Содержание книги
Поиск на нашем сайте
Производная по напр-ю —предел df(x0,y0)/de→ =limt→0+0 f(xo+tex,y0+tey)-f(x0,y0)/t Произв по напр-ю пок-ет на сколько быстро ф-я изменяется при движении вдоль заданного направления. Так как произв пок-ет скорость изм-я ф-и, то можно сказать, что
f’(M)=F Y(M)*V1+F Y(M)*V2/ Градиент-вектор, координаты которого равны соответствующим частным производным данной функции в точке M. gradf(m)=(f x(m);f y(m)) z=5x3y2-x Пр. Пусть z=f(x;y) = 3х+5у+6. Тогда grad z = {3;5} – направл роста ф-и – вектор нормали. Основное свойство градиента: Вектор-градиент направлен в сторону наискорейшего возрастания функции в данной точке. grad (C · f) = C · grad f, grad (f + g) = grad f + grad g, grad (f · g) = g · grad f + f · grad g, grad f/g = g · grad f − f · grad g/g2 35. Сформулируйте теорему о наибольшем и наименьшем значениях дифференцируемой функции на замкнутом ограниченном множестве. Приведите пример. Пусть ф-я u = f (x1, x2,…, xn) опр-на и непрерывна в нек- огр-ом и замкнутом мн-ве D и имеет на этом мн-ве конечные част производные (за искл, быть может, отд точек). Тогда эта ф-я достигает на D своего наиб и наим зн-я (см. св-ва непрерывных ф-й). Если это знач дост-ся во внутр точке мн-ва, то, очевидно, эта точка д быть стац; кроме того, наиб и наим зн-е может дост-ся на границе мн-ва D. Поэтому для опр-ия наиб и наимо зн-й ф-и на мн-ве D треб-ся: 1) найти стац точки ф-и, принадлежащие D, и выч-ть зн-я ф-и в этих точках; 2)найти наиб и наим зн-е, принимаемое ф-ей на границе мн-ва D;3) выбрать наим и наиб из полученных чисел, кот-е и будут являться наим- и наиб- зн-ми ф-и на всем мн-ве D. Пример. Найдем наиб зн ф z = sin x + sin y – sin (x + y) в треуг-ке со сторонами х = 0, у = 0, х + у = 2π. Стац точки опр-ся из решения системы 36. Дайте опр- частных производных высших порядков ф-и двух перем. Сформ теорему о равенстве смешанных производных и приведите в качестве ее иллюстрации пример. Пусть D – открытое множество в R 2, f(x,y) – определенная на множестве D ф-я. Предположим, что в каждой точке М ÎD существуют частные производные f ‘x и f ‘y. Тогда частные производные f ‘x(x,y) и f ’y(x,y) естественно считать ф-ми с обл опр D Они наз-ся частными производными пер-го порядка. Част производные от ф-й f ‘x(x,y) и f ’y(x,y) наз-ся част производными вт-го порядка от ф-и f(x,y). Част производные от част производных вт-го порядка наз-ся част производными т-го порядка и т.д. Если первая производная ф-и z= f(x,y) была взята скажем, по x, то ее частные производные в (x0,y0) обозн-ся так:
Продолжая дифф-ть полученные рав-ва, получим частные произв более высоких порядков. Определение. Частные производные вида Теорема. Если производные f²xy(x,y) f²yx(x,y) существуют в некоторой окрестности точки М(x0,y0) и непрерывны в самой точке М, то имеет место равенство: Пример: Док-ть справедливость теоремы (част производные высших порядков не зависят от порядка дифф-ия) для f (x;y) = x3–3y3+5xy2 Проверка: f 'x=3x2+5y2 f 'y=10xy–9y2 f ''xy=10y f ''yx=10y. Теорема спр-ва. 37. Дайте опр экстремума функции двух переменных. В чем состоит необходимое и достаточное условия экстремума. Проиллюстрируйте это на примере. Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0(х0, у0) верно неравенство
Определение. Если для функции z = f(x, y), определенной в некот обл, в некот окр-ти точки М0(х0, у0) верно нерав-во Теорема. (Необ-ые условия экс). Если ф-я f(x,y) в точке (х0, у0) имеет экс, то в этой точке либо обе ее част производные первого порядка равны нулю Теорема. (Дост усл-я экст-) Пусть в окр-ти крит точки (х0, у0) ф-я f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:
1) Если D(x0, y0) > 0, то в точке (х0, у0) функция f(x, y) имеет экстремум, если
2) Если D(x0, y0) < 0, то в точке (х0, у0) функция f(x, y) не имеет экстремума В случае, если D = 0, вывод о наличии экстремума сделать нельзя. 38. Дайте опр-я условных максимума и минимума функции двух переменных. В чем состоит метод множителей Лагранжа для нахождения условных максимума и минимума функции двух переменных. Приведите пример. Определение: Точка М0 = (x0, y0) Î U называется точкой условного максимума (минимума), если существует ε – окрестности точки М0, что для всех M(x,y) из этой ε – окр-и, удовлетворяет условию g(x,y) = C, выполняется неравенство z0 = f(x0,y0) ≥ z = f(x,y) или соответственно z0 = f(x0,y0) ≤ z = f(x,y). Опр-е. Ф-й Лагранжа для ф-и z = f(x,y) наз-ся выражение вида L = (x,y,t) = f(x,y) – t(g(x,y)-c), где t наз-ся множителем Лагранжа Теорема: Если M0(x0,y0) – точка усл экс ф-и z = f(x,y) при g(x,y) = c, то сущ-ет такое t=t0, что точка (x0,y0,t0) будет точкой экс ф-и Лагранжа. Алгоритм нахождения точки условного экстремума: 1.Найти критические точки функции Лагранжа, т.е. решить систему уравнений L'x = f'x + tg'x = 0, L'x = f'y + tg'y = 0, L't = g – c =0 2.Составим определитель 0 g'x g'y ∆ = g'x L''xx L''xy g'y L''yx L''yy 3.Вычислить ∆ в критических точках. Если ∆>0, то f(x,y) имеет условный максимум. Если ∆<0, то f(x,y) имеет условный минимум. Пример Найти точки условного экстремума функции z = x2 + y2 при x + y = 1. 1.Функция Лагранжа L(x,y,t) = (x2+y2)t + t(x+y -1) 2.Критические точки L'x=2x+t=0, L'y=2y+t=0, L't=x+y-1=0, Следовательно (x0=1/2, y0=1/2, t0=-1) 3.Вид условного экстремума g'x= (x+y)'x=1, g'y=(x+y)'y=1, L'xx=2, L'xy=0, L'yy=2 ∆= 0 1 1 = -4<0 1 2 0 1 0 2 То M0 (1/2, ½) –точка условного минимума. 39. Дайте опр однородной ф-и двух аргументов и сфор теорему Эйлера. Явл-я ли ф-я Однородная ф-я – ф-я одного или неск переменных, удовлетворяющая след условию: при одновременном умножении всех аргументов ф-и на один и тот же (произвольный) множитель зн-е ф-и умножается на некот степень этого множ-ля, т. е. для однородной ф-и двух аргументов f (x, y) при всех зн-ях х, у и любом λ должно иметь место рав-во: f (λ x, λ у) = λn f (х, y), где n — т.н. степень однор-ти. Т Эйлера: если в выражении полного диф-ла
40. Дайте определение выпуклой функции двух аргументов и приведите критерий выпуклости. Проиллюстрируйте это на примере. Множество называется выпуклым, если вместе с любыми своими точками
Более того, экстремум выпуклой ф-и явл-ся глобальным, то есть наим-м зн-ем во всей области определения в случае функции, выпуклой вниз, и наиб-им в случае функции, выпуклой вверх. Теорема. Если ф-я Пример: Исследовать на выпуклость и вогнутость: Найдем критические точки: Исследуем эти точки, для этого найдем частные производные: Исследуем точку M 1: а) А =6 х (М 1=0 ), В = –6 (М 1 = –6 ), С =48 у (М 1=0 ) ∆(М 1)= АС – В 2= –36 < 0. В точке М 1 нет экстремума, т.к. ∆<0. Исследуем точку M 2: б) А =6 х (М 2=6 ), В = –6 (М 2 = –6 ), С =48 у (М 2=24 ) ∆(М 2)=108 > 0. Т.к. значение A>0, значит в точке М 2 минимум (z min=0). Ф-я выпукла. 41. Дайте определение и перечислите основные свойства неопределенного интеграла, иллюстрируя их примерами. Определение: Если F(x) – первообразная для f(x),то выражение F(x) + C, где С – произволь пост-ая, наз-ся неопределенным интегралом от ф-и f(x). Записывают: Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке. Свойства: 1. 2. Пример 3. 4. Док-во: Это вытекает из того, что если ф-и U, V и W – первообразные соот-но для u, v и w, то производная их суммы (разности) будет равна сумме (разности) производных. Пример 5.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.23 (0.01 с.) |

 хар-ет быстроту изм-я ф-и
хар-ет быстроту изм-я ф-и  по напр-ию
по напр-ию  в точке
в точке  . Если напр-е
. Если напр-е  совпадает с полож-ым напр-ем оси Ох, то
совпадает с полож-ым напр-ем оси Ох, то 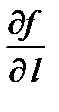 есть част производная ф-и
есть част производная ф-и  по х в точке
по х в точке  . Если
. Если  совпадает с полож направлением оси Оу, то
совпадает с полож направлением оси Оу, то 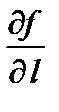 есть частная производная функции
есть частная производная функции 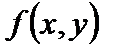 по у в точке
по у в точке  .
.
 , откуда
, откуда 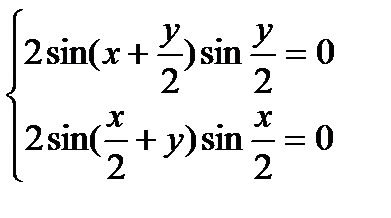 . Един-ой внутр точкой дан тр-ка, являющейся реш-м получ сис-мы, будет
. Един-ой внутр точкой дан тр-ка, являющейся реш-м получ сис-мы, будет  , в кот
, в кот  . Это зн-е оказывается наиб и на всем рассм-ом мн-ве, так как на его границе z = 0.
. Это зн-е оказывается наиб и на всем рассм-ом мн-ве, так как на его границе z = 0.



 и т.д. называются смешанными частными производными.
и т.д. называются смешанными частными производными. .
. то точка М0 называется точкой максимума.
то точка М0 называется точкой максимума. то точка М0 называется точкой минимума
то точка М0 называется точкой минимума , либо хотя бы одна из них не существует.Эту точку (х0, у0) будем называть критической точкой.
, либо хотя бы одна из них не существует.Эту точку (х0, у0) будем называть критической точкой. D=Determinant=∆
D=Determinant=∆ - максимум, если
- максимум, если  - минимум.
- минимум. однородной, и если да, то какова степень одн-ти?
однородной, и если да, то какова степень одн-ти? ф-и f (x, у) заменить диф-ал каждого независимого переменного самим этим переменным, то получают ф-ю f (x, у), умноженную на степень однородности, т.е.:
ф-и f (x, у) заменить диф-ал каждого независимого переменного самим этим переменным, то получают ф-ю f (x, у), умноженную на степень однородности, т.е.: 

 Степень однородности равна (–4).
Степень однородности равна (–4). и
и 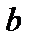 оно целиком содержит отрезок
оно целиком содержит отрезок 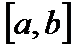 .
.  множества В, лежат не выше хорды, соединяющей точки
множества В, лежат не выше хорды, соединяющей точки  (рис. 12). Анал-но можно дать геом-ое толкование вып вверх ф-и двух переменных.
(рис. 12). Анал-но можно дать геом-ое толкование вып вверх ф-и двух переменных. Очевидно, выпуклая ф-я не может иметь седловых точек (точек перегиба). Это зн-ит, что для вып ф-и рав-во нулю частных производных явл-я не только необ усл экс-, но и дост.
Очевидно, выпуклая ф-я не может иметь седловых точек (точек перегиба). Это зн-ит, что для вып ф-и рав-во нулю частных производных явл-я не только необ усл экс-, но и дост. выпукла (вогнута) во всей обл определения D, тогда она имеет не более одной точки глобального минимума (максимума) в области D.
выпукла (вогнута) во всей обл определения D, тогда она имеет не более одной точки глобального минимума (максимума) в области D.



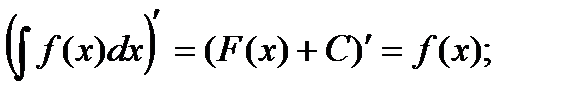 Пример
Пример 
 Доказательство:
Доказательство: 

 Пример
Пример 
 где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.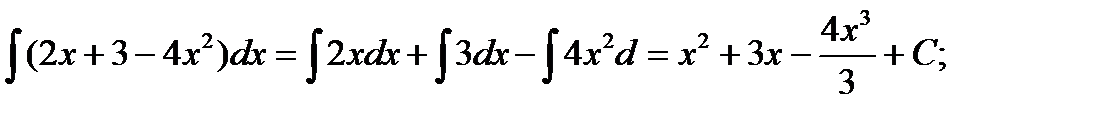
 Пример
Пример 



