
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 13 Импликация высказываний и ее свойства .Обратная, противоположная и обратная противоположной импликации.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Импликацией двух высказываний A и B называется новое высказывание A=>B(из А следует В, если А то В),которое ложно только в том случаи, когда А-ИСТИНА,В-ложь, во всех остальных случаях! Импликация-истина
Свойства: 1.закон контропозиции A=>B ó
Если дана импликация A=>B,то импликация В=>A называется обратной Эквиваленция высказывания - …двух высказ. a и b,называется новое высказывание A<=>B,которые истинно, если высказывание A и B одновременно И или Л(тоесть принимают одинаковые значения)
17. Отрицание предиката. Множество истинности отрицания предиката. Примеры. Отрицанием предиката А(х) называется предикат Справедливо равенство:
ТА = ТА’, где ТА’ – дополнение множества ТА до множества Х
26.Особенности математических понятий. Объём и содержание понятий. Видо-родовые отношения между понятиями. Всякий математический объект обладает определенными свойствами. Например, квадрат имеет 4 стороны, 4 прямых угла, равные диагонали(существенные). Среди свойств объекта различают свойства существенные и несущественные для его выделения из других объектов. Свойство считают существенным для объекта, если оно присуще этому объекту и без него он не может существовать. Несущественные свойства – это такие свойства, отсутствие которых не влияет на существование объекта. Примеры: *существенные: см. выше Несущественные: сторона АВ квадрата горизонтальна (если квадрат повернуть, то сторона окажется расположенной по-другому). Поэтому, чтобы понимать, что представляет собой данный объект достаточно знать его существенные свойства. В этом случае говорят, что имеется понятие об этом объекте. Совокупность всех взаимосвязанных существенных свойств объекта называют содержанием понятия об этом объекте. Когда говорят о математическом объекте, то обычно имеют в виду всю совокупность объектов, обозначаемых одним термином. Так, когда говорят о квадрате, то имеют в виду все геометрические фигуры, являющиеся квадратами. Совокупность всех квадратов составляет объем понятия квадрата. Объем понятия – это совокупность всех объектов, обозначаемых одним и тем же термином. Т. о., всякое понятие характеризуется термином, объемом и содержанием. Связь объема и содержания: Чем больше объем понятия, тем меньше его содержание, и наоборот. Так например объем понятия «прямоугольный треугольник» меньше объема понятия «треугольник», поскольку в объем первого понятия входят не все треугольники, а только прямоугольные. Но содержание первого понятия больше: прямоугольный треугольник обладает не только всеми свойствами треугольника, но и другими, присущими только ему (сумма двух острых углов прямоугольного треугольника = 90 градусов; катет, лежащий против угла 30 градусов = половине гипотенузы) 14.Высказывания и высказывательные формы. Область определения и множество значений истинности предиката. Примеры. Определение. Высказывание - повествовательное предложение, относительно которого имеет смысл говорить истинно оно или ложно. Логическими значениями высказываний являются «истина» и «ложь». Примеры высказываний: · Москва стоит на Неве. (ложно –Л; простое) · Лондон — столица Англии. (истинно – И; простое) · Сокол не рыба. (истинно – И; сложное) · Число 6 делится на 2 и на 3. (истинно – И; сложное) Различают два вида высказываний: ü Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. ü Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если.... то...», «тогда и только тогда», принято называть сложными или составными. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным. Определение. Высказывательной формой или предикатом называется предложение с одной или несколькими переменными, обращающееся в высказывание, если вместо переменных подставить их значения. Определение. Совокупность значений переменной х, которая может не обязательно иметь числовую природу, называется областью определения предиката. Определение. Значения х, обеспечивающие истинность предиката, называются его множеством истинности. 18.Отношение логического следования предикатов. Импликацией - двух предикатов Р(х) и К(у) называется предикат обозначаемый Р(х) -> К(у), который ложен когда Р(х)-истина, К(у)-ложь.
Импликацией (следованием) - двух предикатов Р(х) и К(х) называется когда предикат обозначаемый Р(х) -> К(х), если Р(х) обращается в истинное высказывание при всех х которых К(х)- превращается в истинное высказывание. Р(х) ТР- область истинности К(х) ТК- область истинности Р(х) -> К(х) ТР с ТК. 19.Отношение равносильности предикатов. Примеры. Эквиваленцией (равносильность) - двух предикатов Р(х) и К(у)называется предикат обозначаемый Р(х) <-> К(у),который истин,когда оба предиката принимают одинаковые истинностные значения.(два предиката равносильны, когда из одного следует другой, и наоборот.) Р(х) <-> К(у) ТР=ТК. 20.Кванторы существования и общности и их влияние на предикаты. В формулировках математических предложений часто встречаются слова «каждый», «все», «некоторые», «хотя бы один» и др. Такие выражения называются кванторами. Выражение «для каждого х»(для всякого,для всех) называется –квантором общности. Пусть Р(х) одноместный предикат,приписывание к нему символа (Vх) (А перевернутая) называется – операцией навешивания квантора общности, её результатом является утверждение (Vх) Р(х),которое представляет собой запись высказывания о тождественности предиката Р(х) В(х): х- четное число. (Vх (А перевернутая) принадлежит R) х- четное число-Л При помощи добавления квантора предикат обращается в высказывание истинное или ложное. Выражение «существует х такое, что…»- называется квантором существования. Пусть Р(х) одноместный предикат,приписывание к нему символа Е(х) (Е в другую сторону) называется – операцией навешивания квантора существования, её результатом является утверждение (Ех) Р(х),которое представляет собой запись высказывания о выполнимости предиката Р(х). В(х): х- четное число. (Е(х) (Е в другую сторону) принадлежит R) х- четное число-И. А) для того что бы доказать истинность высказывания с квантором общности необходимо провести некоторое доказательство, а что бы его опровергнуть достаточно привести один контрпример. В) что бы доказать истинность высказывания с квантором существования достаточно привести один пример,а что бы показать его ложность нужно провести доказательство. Построение отрицания высказывания с кванторами. Для того что бы построить отрицание высказывания с квантором общность (существования) достаточно заменить его квантором существования(общности) и построить отрицание предложения стоящего после квантора. Например: (Е(х) (Е в другую сторону) принадлежит R) х- однозначное число, х:10. Все однозначные числа не делятся на 10. (Vх (А перевернутая) принадлежит R) х- однозначное число,х не: 10. 21.Построение отрицания высказываний с кванторами.
Построение отрицания высказывания с кванторами. Для того что бы построить отрицание высказывания с квантором общность (существования) достаточно заменить его квантором существования(общности) и построить отрицание предложения стоящего после квантора. Например: (Е(х) (Е в другую сторону) принадлежит R) х- однозначное число, х:10. Все однозначные числа не делятся на 10. (Vх (А перевернутая) принадлежит R) х- однозначное число,х не: 10. Законы отрицания. (Vх) Р(х)(с чертой)= (Ех) Р(х) (Р с чертой) (Ех) Р(х)(с чертой)= (Vх) Р(х)(Р с чертой)
22.Теорема: определение, виды. Закон контрапозиции. Необходимое и достаточное условия. Критерий. Примеры. Определение: ТЕОРЕМА (греч. theorema, от theoreo - рассматриваю), в математике - предложение (утверждение), устанавливаемое при помощи доказательства (в противоположность аксиоме). Теорема обычно состоит из условия и заключения. Напр., в теореме: если в треугольнике один из углов прямой, то два других - острые, после слова ''если'' стоит условие, а после ''то'' - заключение.
Рассмотрим, например, теорему «если четырехугольник является прямоугольником, то в нем диагонали равны». Построим предложение, обратное данному: «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником». Это ложное высказывание, в чем легко убедиться (в равнобедренной трапеции диагонали равны, но трапеция не является прямоугольником).
Рассмотрим теорему «в равнобедренном треугольнике углы при основании равны». Обратное ей предложение таково: «если в треугольнике углы при основании равны, то этот треугольник – равнобедренный». Это истинное предложение и потому является теоремой. Ее называют теоремой, обратной данной.
Для всякой теоремы вида А
Вообще, для какой бы теоремы мы ни формулировали предложение, обратное противоположному, оно всегда будет теоремой, потому что имеется следующая равносильность: (А
Эту равносильность называют законом контрапозиции.
1. В следующих теоремах выделим условие и заключение: а) «Для того чтобы разность двух чисел делилась на 2, достаточно, чтобы на 2 делилось уменьшаемое и вычитаемое»;
б) «Для того чтобы четырехугольник был квадратом, необходимо, чтобы хоты бы один из его углов был прямым». Решение: а) Слово достаточно относится к предложению «уменьшаемое и вычитаемое делится на 2», следовательно, это предложение и является условием теоремы. Тогда заключение теоремы – «разность двух чисел делится на 2». б) В данной теореме есть слово «необходимо», которое относится к предложению «чтобы четырехугольник был квадратом». Значит, это и будет условием данной теоремы. А ее заключением в таком случае будет предложение «один из углов четырехугольника прямой». 2. Сформулируем следующие теоремы в виде «если …, то …»: а) «Перпендикуляр к одной из двух параллельных прямых также перпендикуляр к другой»; б) «Всякий параллелограмм имеет центр симметрии». Решение: а) Выделим условие и заключение теоремы: «Перпендикуляр к одной из двух параллельных прямых» – условие, «перпендикуляр к другой» – заключение. Тогда теорема примет вид: «Если есть перпендикуляр к одной из двух параллельных прямых, то он является также перпендикуляром к другой прямой». б) Условие теоремы – «всякий параллелограмм», заключение – «имеет центр симметрии». Нашу теорему тогда можно переформулировать следующим образом: «Если фигура параллелограмм, то она имеет центр симметрии».
3. Дана теорема: «Если в четырехугольнике две противоположные стороны равны и параллельны, то четырехугольник параллелограмм». Сформулируем предложения, являющиеся обратным, противоположным и обратно противоположным.
Решение: Выделим условие и заключение данной теоремы. Условие: «в четырехугольнике две противоположные стороны равны и параллельны». Заключение: «четырехугольник – параллелограмм».
Заменяя условие и заключение исходной теоремы их отрицаниями, получим теорему, противоположную данной: «Если в четырехугольнике две противоположные стороны не равны или не параллельны, то четырехугольник – не параллелограмм». Это предложение также истинно.
Зако́н контрапози́ции — закон классической логики, утверждающий, что в том случае, если некая посылка A влечёт некое следствие B, то отрицание этого следствия (то есть «не B») влечёт отрицание этой посылки (то есть «не A»). Как и всякое общезначимое импликативное утверждение, может служить также и правилом вывода. В виде формулы алгебры высказываний закон контрапозиции имеет вид
Необходимое условие Необходимыми условиями истинности утверждения А называются условия, без соблюдения которых А не может быть истинным. Суждение P является необходимым условием суждения X, когда из (истинности) X следует (истинность) P. То есть, если P ложно, то заведомо ложно и X. Для суждений X типа «объект принадлежит классу M» такое суждение P называется свойством (элементов) M. Достаточное условие Достаточными называются такие условия, при наличии (выполнении, соблюдении) которых утверждение А является истинным. Суждение P является достаточным условием суждения X, когда из (истинности) P следует (истинность) X, то есть в случае истинности P проверять X уже не требуется. Для суждений X типа «объект принадлежит классу M» такое суждение P называется признаком (элементов) M.
Критерий — это фактор, на основании которого вы судите о чём-либо или принимаете решение. Критерий истинности. Критерий отбора победителей. Соответствовать критериям. Крите́рий — признак, основание, правило принятия решения по оценке чего-либо на соответствие предъявленным требованиям (мере). Особо выделяют критерии истинности знания. Различают логические (формальные) и эмпирические (экспериментальные) критерии истинности. Формальным критерием истины служат логические законы: истинно всё, что не заключает в себе противоречия, логически правильно. Эмпирическими критериями истинности служит соответствие знаний экспериментальным данным, например: «критерий пригодности объекта», «критерий превосходства объекта», «критерий достоверности результатов», «критерий достаточности испытаний». Вопросом о критериях истины, выставляемых разными философскими школами, занимается теория познания или гносеология.
23.Умозаключения и их виды. Умозаключение это способ получения нового знания на основе некоторого имеющегося. Умозаключение состоит из посылок и заключений. Посылка- это высказывание, содержащее знание. Заключение – это высказывание, содержащее новое знание, полученное из исходного. В умозаключении из посылок выводится заключение. Существуют разные виды умозаключений: например: Существуют дедуктивные умозаключения- это умозаключения, в котором посылки и заключение находятся в отношении логического следования.
Если посылки дедуктивного умозаключения обозначить А1,А2,А3,…..Аn, а заключение В, то само умозаключение можно представить в виде А1,А2,…Аn->В,но чаще это записывают следующим образом А1,…. Аn\В(А над чертой В од чертой)черта означает = следовательно.
Правильность умозаключений определяется только его формой и не зависит от содержания входящих в него утверждений.
Существует правило,соблюдая которое можно строить дедуктивные умозаключения, эти правила называются правилами вывода или схемами дедуктивных умозаключений, таких правил много,но наиболее часто используются следующие: 1) Правило заключения. А(х)=>В(х),А(а)\В(а)(над \ под чертой) В нем даны две посылки первая - А(х)=>В(х),это общая посылка, А(а) вторая- частная посылка, она получается из условия А(х) в случае когда х=а Предложение В(а) это умозаключение, оно получается из В(х) при х=а. Рассмотрим пример: Если запись числа х оканчивается цифрой 5, то число х делиться на 5. Запись числа 275 оканчивается на 5 =>275:5(А(х)-х оканчивается 5, В(х),х:5, А(а)-275 оканчивается на 5, В(а) 275:5) Существуют различные способы проверки правильности умозаключений Рассмотрим способ с использованием кругов Эйлера. А(х)=>В(х),А(а)\В(а)(над \ под чертой) А(х)=>В(х),--- ТА с ТВ А(а) а принадлежит ТА В(а) а принадлежит ТВ. ТА с ТВ, а принадлежит ТА\ а принадлежит ТВ.(над \ под чертой) В кругах в ТВ круг- ТА, а в нем точка а. 20 правило отрицания. А(х)=>В(х),отриц В(а)\отриц А(а) (над \под чертой.) Пример: Если запись числа х оканчивается на5, то число х делиться на 5, число 137 не делиться на 5 следовательно он не оканчивается на5. А(х)=>В(х)- ТА с ТВ, отриц В(а) а принадлежит ТотрицВ=Т’В, отриц А(а)- а принадлежит ТотрицА,= Т’А. ТА с ТВ, а принадлежит ТотрицВ=Т’В\ а принадлежит ТотрицА,= Т’А. В кругах- ТА в пустом,и это все 2 круга в ТВ,в ТВ и точка а. 3) правило силлогизма. А(х)=>В(х), В(х)=>С(х)\ А(х)=>С(х). Пример: если число делиться на 12, то оно делиться на 6. Если число делиться на 6, то оно делиться на 3 следовательно если число х делиться на 12,то он делиться на 3.
А(х); х: 12 В(х) х:6 С(х):х:3 А(х)=>В(х), ТА с ТВ, В(х)=>С(х),ТВ с ТС, А(х)=>С(х), ТА с ТС. ТА с ТВ, ТВ с ТС\ ТА с ТС. В кругах. ТА в ТВ и все в ТС. При помощи кругов Эйлер можно проверить является ли умозаключение дедуктивным, если оно выполнено по схеме отличающейся от рассмотренных правил. Например: Если запись числа х оканчивается цифрой 5, то число х делиться на 5. Запись числа 125 делиться на 5 =>125 оканчивается на 5(А(х)-х оканчивается 5, В(х),х:5, В(а) 275:5, А(а)-125 оканчивается на 5) А(х)=>В(х),В(а)\А(а)(над \ под чертой) А(х)=>В(х), ТА с ТВ, А(а) а принадлежит ТА,В(а) а принадлежит ТВ. ТА с ТВ, а принадлежит ТВ \ а принадлежит ТА. В кругах точка а в ТВ и там же круг ТА. Данное умозаключение не является дедуктивным, т.к не гарантирует истинности заключения. При анализе умозаключения, заключение может быть истинным, а умозаключение не быть дедуктивным. При выполнении умозаключения можно менять очередность посылок и если общие посылки в правилах дедуктивных умозаключений содержат больше одной переменной, то это не нарушает смысла этих правил.
Кроме дедуктивных существуют другие виды умозаключений 1) неполная индукция- это умозаключение, в котором на основании того что некоторые объекты класса обладают определенным свойством, делается вывод о том, что все объекты данного класса обладают этим свойством. Рассуждая по схеме не полной индукции можно придти к ложному выводу. Например: Рассмотрим 3+5 и 3х5, 2+7 и 2х7, 4+8 и 4х8 3+5меньше 3х5 и так каждое! Т.е для некоторых натуральных чисел их сумма меньше их произведения на основании этого делают вывод о том, что этим свойством обладают все натуральные числа, т.е для любых чисел а и в натуральных а+в меньше ахв. Это не верно т.к можно привести контр пример, где данное неравенство не выполняется. 1+2 и 1х2, первое больше второго! К выводам полученным при помощи неполной индукции надо относиться критически, т.к они носят характер предположения, гипотезы и нуждаются в доказательстве. 2)аналогия.- аналогией называют умозаключения, в котором на основании сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии признака такого же характера у другого объекта. Вывод по аналогии носит характер предложения и нуждается в доказательстве или опровержении. Например: ученик установил, что число делиться на 6 если оно делиться на 2 и3. Действуя по аналогии он сделал вывод, что число делиться на 8 если оно делиться на2 и 4. И этот вывод является ложным, контрпример 12 или 20!
24.Схемы дедуктивных умозаключений. Существуют дедуктивные умозаключения- это умозаключения, в котором посылки и заключение находятся в отношении логического следования.
Если посылки дедуктивного умозаключения обозначить А1,А2,А3,…..Аn, а заключение В, то само умозаключение можно представить в виде А1,А2,…Аn->В,но чаще это записывают следующим образом А1,…. Аn\В(А над чертой В од чертой)черта означает = следовательно.
Правильность умозаключений определяется только его формой и не зависит от содержания входящих в него утверждений.
Существует правило,соблюдая которое можно строить дедуктивные умозаключения, эти правила называются правилами вывода или схемами дедуктивных умозаключений, таких правил много,но наиболее часто используются следующие: 1) Правило заключения. А(х)=>В(х),А(а)\В(а)(над \ под чертой) В нем даны две посылки первая - А(х)=>В(х),это общая посылка, А(а) вторая- частная посылка, она получается из условия А(х) в случае когда х=а Предложение В(а) это умозаключение, оно получается из В(х) при х=а. Рассмотрим пример: Если запись числа х оканчивается цифрой 5, то число х делиться на 5. Запись числа 275 оканчивается на 5 =>275:5(А(х)-х оканчивается 5, В(х),х:5, А(а)-275 оканчивается на 5, В(а) 275:5) Существуют различные способы проверки правильности умозаключений Рассмотрим способ с использованием кругов Эйлера. А(х)=>В(х),А(а)\В(а)(над \ под чертой) А(х)=>В(х),--- ТА с ТВ А(а) а принадлежит ТА В(а) а принадлежит ТВ. ТА с ТВ, а принадлежит ТА\ а принадлежит ТВ.(над \ под чертой) В кругах в ТВ круг- ТА, а в нем точка а. 20 правило отрицания. А(х)=>В(х),отриц В(а)\отриц А(а) (над \под чертой.) Пример: Если запись числа х оканчивается на5, то число х делиться на 5, число 137 не делиться на 5 следовательно он не оканчивается на5. А(х)=>В(х)- ТА с ТВ, отриц В(а) а принадлежит ТотрицВ=Т’В, отриц А(а)- а принадлежит ТотрицА,= Т’А. ТА с ТВ, а принадлежит ТотрицВ=Т’В\ а принадлежит ТотрицА,= Т’А. В кругах- ТА в пустом,и это все 2 круга в ТВ,в ТВ и точка а. 3) правило силлогизма. А(х)=>В(х), В(х)=>С(х)\ А(х)=>С(х). Пример: если число делиться на 12, то оно делиться на 6. Если число делиться на 6, то оно делиться на 3 следовательно если число х делиться на 12,то он делиться на 3.
А(х); х: 12 В(х) х:6 С(х):х:3 А(х)=>В(х), ТА с ТВ, В(х)=>С(х),ТВ с ТС, А(х)=>С(х), ТА с ТС. ТА с ТВ, ТВ с ТС\ ТА с ТС. В кругах. ТА в ТВ и все в ТС. При помощи кругов Эйлер можно проверить является ли умозаключение дедуктивным, если оно выполнено по схеме, отличающейся от рассмотренных правил. Например: Если запись числа х оканчивается цифрой 5, то число х делиться на 5. Запись числа 125 делиться на 5 =>125 оканчивается на 5(А(х)-х оканчивается 5, В(х),х:5, В(а) 275:5, А(а)-125 оканчивается на 5) А(х)=>В(х),В(а)\А(а)(над \ под чертой) А(х)=>В(х), ТА с ТВ, А(а) а принадлежит ТА,В(а) а принадлежит ТВ. ТА с ТВ, а принадлежит ТВ \ а принадлежит ТА. В кругах точка а в ТВ и там же круг ТА. Данное умозаключение не является дедуктивным, т.к не гарантирует истинности заключения. При анализе умозаключения, заключение может быть истинным, а умозаключение не быть дедуктивным. При выполнении умозаключения можно менять очередность посылок и если общие посылки в правилах дедуктивных умозаключений содержат больше одной переменной, то это не нарушает смысла этих правил.
25.Способы математических доказательств. Примеры. Доказать какое-либо утверждение это значит показать, что это утверждение логически следует из системы истинных и связанных с ним утверждений.
Основным способом математического доказательства является дедуктивный вывод, а само доказательство это цепочка умозаключений, в которых заключение одного из них является посылкой в последующем.
По способу ведения различают прямые и косвенные доказательства.
К прямым можно отнести: полную индукцию- это такой способ при котором истинность утверждения следует из истинности его в частных случаях. Например: доказать, что каждое составное натуральное число больше 4, но меньше 20, можно представить в виде простых чисел. 6=1+5,10=3+7,16=13+3,……. Следовательно, утверждение справедливо.
Примером косвенного –является доказательство методом противного. При этом допускают, что заключение ложно, следовательно, его отрицание истинно. Далее строят цепочку дедуктивных умозаключений до тех пор, пока не получат утверждение противоречащее условию. Как только такое утверждение получено делают вывод, что предложение сделано не верно, т.е верно исходное заключение. 28.Комбинаторные задачи. Виды и формулы для подсчёта числа возможных комбинаций. Часто встречаются задачи, которые имеют несколько различных вариантов решений, при этом необходимо осуществить перебор всех возможных вариантов или подсчитать их число. Задачи, требующие такого решения, называются комбинаторными. В начальной школе такие задачи решаются методом перебора, а для облегчения этого процесса используются таблицы и графики. Вылеляют: 1) Размещение элементов. Правило сумы и произведения- это общие правила решения комбинаторных задач, кроме них пользуются формулами для подсчета комбинаций, которые используются наиболее часто. Определение: Пусть имеется множество, состоящее из n-элементов, в нем выбирают подмножества, состоящие из m- элементов. Размещением из n-элементов, по m- называются картежи составленные из m элементов. В размещении важен не только состав элементов, но и порядок их следования. Пример: 7,4,1= 74,41,47,14,71,14 Пример: учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание н 1-ый день что бы в нем было 4 различных предмета. 1- 8 способов,2-7,3-6,4-5.=1680. Любое расписание на один день отличается либо предметами либо порядком следования предметов. Значит речь идет о размещениях их 8 элементов по 4. Для подсчета количества размещений существуют формулы: а) размещение из n по m с повторениями с волной сверху А по n в степени m = n в степени m. Пример: сколько трехзначных чисел можно составить из цифр 1,2,5,7,8, если цифры в записи могут повторяться? С волной А по 5 в степени 3= 5 в степени3 =125. в) без поторений. А по n в степени m =nх(n-1)…..(n-m+1)/ Пример: сколь…. Если в записи не повторяются А по 5 в степени 3= 5х4х3=60. 2)В данном случае разные числа получаются в результате перестановки цифр, по этому размещение из n по m называют перестановкой из n элементов. Другими словами перестановкой и n элементов называют каждое расположение этих элементов в определенном порядке. Количество перестановок подсчитывается по формуле. P по n= n1=1х2х3……хn 3) сочетание. Пример: имеется 5 роз разног цвета, требуется составить букет из 3х роз. Сколькими способами это можно сделать? 12345 123,235,321 Наборы элементов,в которых важен состав, а порядок не важен называют сочетаниями. Сочетанием из n элементов по m называется любое множество их m элементов взятых из n элементного множества. Формула: С по n в степени m = n!\m!х(n-m)! С по 5 в 3 степени = 10.- Задачи: имеется 5 автомобилей разных марок сколько разлчных кортежей автомашин можно составить Р по5=5!=120. Определение понятий. Способы определения понятий. Правила определения понятий через род и видовое отличие. В содержание понятия о к-л математическом объекте входит много различных существенных свойств этого объекта. Однако чтобы установить, содержится ли объект в объеме данного понятия (распознать его), необходимо проверить наличие у него лишь некоторых существенных свойств. Указание этих существ. св-в объекта, которые достаточны для распознания объекта, называется определением понятия об этом объекте. Определение – это логическая операция, раскрывающая содержание понятия. Способы определения понятия: Прежде всего различают явные и неявные определения. Явные определения имеют форму равенства, совпадения 2-х понятий. Например, прямоуг. треугольник – это треугольник с прямым углом. Если обозначить через а понятие «прямоугольный треугольник», а через в понятие «треугольник с прямым углом», то схема данного определения будет такова: «а есть в». Неявные определения не имеют формы совпадения двух понятий. Примерами таких понятий являются так называемые контекстуальные и остенсивные определения. В контекстуальных определениях содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл вводимого понятия. Например, определение уравнения и его решение. 3 + х = 9, какое число нужно подставить вместо х, чтобы равенство было верным? Это число 6. Из этого текста следует, что уравнение – это равенство с неизвестным числом, которое надо найти, а решить уравнение – это найти такое значение х, при подстановке которого в уравнение получается верное равенство. Остенсивные определения используются для введения терминов путем демонстрации объектов, которые этими терминами обозначают. Поэтому остенсивные определения называют ещё определениями путем показа. Например, таким способом определяются в нач шк понятия равенства и неравенства. 2*7 > 2*6; 78-9 < 78; 37+6 > 37 - это неравенства 9*3 = 27; 6*4 = 4*6; 17-5 = 8+4 – это равенства В явных определениях отождествляют два понятия. Одно из них называют определяемым понятием, другое – определяющим. Через определяющее раскрывается содержание определяемого понятия. Анализ структуры определения квадрата: «Квадратом называется прямоугольник, у которого все стороны равны». Сначала указано определяемое понятие – «квадрат», а затем приведено определяющее, которое включает св-ва: быть прямоугольником, иметь все равные стороны. Свойство «быть прямоугольником» указывает, что все квадраты – прямоугольники, т.е. понятие «прямоугольник» является более общим, чем понятие «квадрат». Его называют родовым по отношению к определяемому понятию «квадрат». Второе свойство – «иметь равные стороны» - это указание видового свойства, которое отличает квадрат от других видов прямоугольника. Схематичная структура определения: Определение понятия по такой схеме называют определением через род и видовое отличие.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 2329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.81.255 (0.014 с.) |

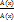 , ТА –
, ТА –
 В (если А, то В) можно сформулировать предложение
В (если А, то В) можно сформулировать предложение 
 (если не А, то не В), которое называют противоположным данному. Но это предложение также не всегда является теоремой. Например, предложение, противоположное теореме «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником» будет ложным: «если четырехугольник не является прямоугольником, то в нем диагонали не равны».
(если не А, то не В), которое называют противоположным данному. Но это предложение также не всегда является теоремой. Например, предложение, противоположное теореме «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником» будет ложным: «если четырехугольник не является прямоугольником, то в нем диагонали не равны».
 (
(  . Также являются тавтологиями следующие похожие формулы:
. Также являются тавтологиями следующие похожие формулы:  ,
,  . При подстановке вместо
. При подстановке вместо  произвольных формул также получаются тавтологии.Закон контрапозиции доказуем в исчислении высказываний,ноприэтомформула
произвольных формул также получаются тавтологии.Закон контрапозиции доказуем в исчислении высказываний,ноприэтомформула  невыводима в интуиционистском исчислении высказываний, где p,q - пропозициональные переменные
невыводима в интуиционистском исчислении высказываний, где p,q - пропозициональные переменные



