
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества, состоящие из чисел, называют числовыми множествами.Содержание книги
Поиск на нашем сайте Этапы решения. и у алгебраического и у арифметического. 1. Восприятие и анализ содержания задачи. 2. Поиск и составления плана решения задачи. 3. Выполнение плана решения. Формулировка вывода о выполнении требования задачи (ответа на вопрос задачи). 4. Проверка решения и устранение ошибок, если они есть. Формулировка окончательного вывода о выполнении требования задачи или ответа на вопрос задачи. Основная цель первого этапа решения – понимание решающим в целом ситуации, описанной в задаче, понимание условий задачи, ее требования или вопроса, смысла всех терминов и знаков, имеющихся в тексте. 35. О. т.з. – есть описание на естественном языке нек.явления, ситуации или процесса с требованием дать кол-ную характеристику к-л компонента этого явления, установить наличие или отсутствие отношений между компонентами или определить вид этого отношения. Основные методы решения – арифметический и алгебраический. О. решить задачу арифм.методом – значит найти ответ на требование задачи при помощи выполнения арифметических действий над числами. (можно решать несколькими способами, они будут отличаться логикой рассуждения). Пример. Сшили 3 платья, расходуя на каждое по 4 метра ткани. Сколько кофт можно сшить из этой ткани, если расходовать на 1 кофту по 2 м. 1. 4*3=12 2. 12:2=6. 1. 4:2=2 2. 3*2=6 О. решить задачу алгебраическим методом – значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений. (тоже можно несколькими способами) Пример. Свитер, шапку и шарф связали из 1кг 200г шерсти, шарф на 100 гр больше шапки и на 400 гр меньше свитера. Сколько шерсти израсх.на каждую вещь? Пусть х-это шарф. Х-(х-100) + (х+400)=1200 3х+300=1200 3х=900 Х=300гр. И т.д. Моделирование при решении текстовых задач. Примеры моделей. О. мат.модель-это описание к-л реального процесса на языке мат.понятий. формул и отношений. Мат.моделью текст.зад.явл.выражение,если з.решается арифметическим методом, и уравнение, если алгебраическим. Этапа мат.моделирования. 1. Перевод условий на мат.язык(выд.необходимые для решения данные и искомые и матем. Способами описывают связи между ними) 2. Внутримодельное решение (решение уравнения или нахождение значения выражения) 3. Интерпритация (перевод полученного решения на язык, на котором была сформулирована исходная задача) Чтобы облегчить 1 этап строят вспомогательные модели. Процесс решения задачи- переход от словесной к вспомогательной модели, а от нее к математической. Виды моделей. 1. Знаковые (должны быть представлены все её объекты, все отношения между ними, указаны требования) Естеств.язык - краткая запись и таблицы. Матем.язык – выражения,уравнения, запись по действиям. Схематизированные Выщ-ные – обеспечивают физическое действие с предметами (спички, пуговицы) Графические – исп.для обобщенного схематического создания ситуации, описанной в задаче (рисунок (обыч.условн.) чертеж(обычн.схематич.)). БИЛЕТ 36. ПОНЯТИЕ АЛГОРИТМА. СВОЙСТВА АЛГОРИТМА. ВИДЫ АЛГОРИТМОВ. СПОСОБЫ ОПИСАНИЯ АЛГОРИТМОВ Алгоритмом называется точное и понятное предписаниe исполнителю совершить последовательность действий, направленных на решение поставленной задачи. Слово «алгоритм» происходит от имени математика Аль Хорезми, который сформулировал правила выполнения арифметических действий. Первоначально под алгоритмом понимали только правила выполнения четырех арифметических действий над числами. В дальнейшем это понятие стали использовать вообще для обозначения последовательности действий, приводящих к решению любой поставленной задачи. Говоря об алгоритме вычислительного процесса, необходимо понимать, что объектами, к которым применялся алгоритм, являются данные. Алгоритм решения вычислительной задачи представляет собой совокупность правил преобразования исходных данных в результатные. Основными свойствами алгоритма являются: 1.детерминированность (определенность). Предполагает получение однозначного результата вычислительного процecca при заданных исходных данных. Благодаря этому свойству процесс выполнения алгоритма носит механический характер; 2.результативность. Указывает на наличие таких исходных данных, для которых реализуемый по заданному алгоритму вычислительный процесс должен через конечное число шагов остановиться и выдать искомый результат; 3.массовость. Это свойство предполагает, что алгоритм должен быть пригоден для решения всех задач данного типа; 4.дискретность. Означает расчлененность определяемого алгоритмом вычислительного процесса на отдельные этапы, возможность выполнения которых исполнителем (компьютером) не вызывает сомнений. Алгоритм должен быть формализован по некоторым правилам посредством конкретных изобразительных средств. К ним относятся следующие способы записи алгоритмов: словесный, формульно-словесный, графический, язык операторных схем, алгоритмический язык. Способами представления алгоритмов, изучаемыми в информатике, являются: естественный язык для словесно-пошагового способа записи алгоритма; язык блок-схем как графический способ записи алгоритма; языки программирования. Рассмотрим все три способа записи алгоритма на примере решения конкретной задачи. Задача. Найти площадь прямоугольника по двум его сторонам. Решение: обозначим стороны прямоугольника переменными a и b, а его площадь переменной S. Формула площади прямоугольника S=a*b. Теперь составим алгоритм решения данной задачи для компьютера и запишем его тремя способами. Из выше изложенного ясно, что для того чтобы вычислить площадь прямоугольника, компьютеру необходимо «знать» чему равны переменные a и b. Только тогда он сможет вычислить площадь по формуле. Чтобы алгоритм удовлетворял свойству массовости, необходимо, чтобы переменные a и b вводились с клавиатуры пользователем во время работы алгоритма. После того как компьютер вычислит площадь по формуле, он должен вывести значение переменной S на экран, чтобы пользователь увидел результат работы алгоритма Графический способ записи алгоритма: Блок-схема - графический способ, c помощью которого можно описать алгоритм, где каждый шаг изображается в виде связанных блоков (геометрических фигур). Пуск – останов (овал). Таким блоком, как правило, начинается и заканчивается блок-схема Процесс (прямоугольник). В таких блоках производят вычисления или описывают простые шаги. Ввод-вывод (параллелограмм). Таким блоком обозначают шаги по вводу исходных данных и выводу результатов. Условие (ромб). Осуществляет проверку условий.
При всем многообразии алгоритмов решения задач в них можно выделить три основных вида вычислительных процессов: линейный; ветвящийся; циклический. Линейным называется такой вычислительный процесс, при котором все этапы решения задачи выполняются в естественном порядке следования записи этих этапов. Ветвящимся называется такой вычислительный процесс, в котором выбор направления обработки информации зависит от исходных или промежуточных данных (от результатов проверки выполнения какого-либо логического условия). Циклом называется многократно повторяемый участок вычислений. Вычислительный процесс, содержащий один или несколько циклов, называется циклическим. По количеству выполнения циклы делятся на циклы с определенным (заранее заданным) числом повторений и циклы с неопределенным числом повторений. Количество повторений последних зависит от соблюдения некоторого условия, задающего необходимость выполнения цикла. При этом условие может проверяться в начале цикла — тогда речь идет о цикле с предусловием, или в конце — тогда это цикл с постусловием. БИЛЕТ 30. Перестановки из n элементов. Применение при решении задач. Решение. Получатся наборы: ББ, БА, БР, АА, АБ, АР, РР, РБ, РА. По формуле (3.2) получаем: !!! Размещение с повторениями или выборка с возвращением — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. БИЛЕТ 33. Сочетаниями из n элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов). Число сочетаний без повторений (n различных элементов, взятых по m) вычисляется по формуле:
Число сочетаний c повторениями (n элементов, взятых по m, где элементы в наборе могут повторяться) вычисляется по формуле:
Пример. Возьмем буквы Б, А, Р. Какие сочетания из этих букв, взятых по две, можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) можно брать по два одинаковые буквы. Решение.
Получатся наборы: БА (БА и АБ - один и тот же набор), АР и РБ По формуле
Получатся наборы: ББ, БА, БР, АА, АР, РР. Поформуле
Пример. Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно сделать? Решение. Надо выбрать двух человек из 20. Ясно, что от порядка выбора ничего не зависит, то есть Иванов-Петров или Петров-Иванов - это одна и та же пара дежурных. Следовательно, это будут сочетания из 20 по 2.
По формуле
Пример. В хлебном отделе имеются булки белого и черного хлеба. Сколькими способами можно купить 6 булок хлеба? Решение. Обозначая булки белого и черного хлеба буквами Б и Ч, составим несколько выборок: ББББББ, ББЧЧББ, ЧЧЧЧЧБ,... Состав меняется от выборки к выборке, порядок элементов несущественен, значит это - сочетания с повторениями из 2 по 6. По формуле Cделаем проверку и выпишем все варианты покупки: ББББББ, БББББЧ, ББББЧЧ, БББЧЧЧ, ББЧЧЧЧ, БЧЧЧЧЧ, ЧЧЧЧЧЧ. Их действительно 7. Билет №8 Понятие разбиения множества на классы. Виды классификаций. Примеры. Опр: Говорят, что множество Х разбито на классы Х1, Х2, …, Хn, если выполняются 2 условия: 1)Классы попарно не пересекаются Х1 ÇХ2 Ç…Ç Хn = Æ 2)Объединение всех подмножеств совпадает с множеством Х Х1 È Х2 È … È Хn = Х Если хотя бы 1 из условий не выполняется, то данные разбиения на подмножества не являются разбиением на классы. Рассмотрим множество N, его элементы обладают разными свойствами, и выделим числа, которые обладают свойством «быть кратным 5». Это свойство выделяет в множестве N подмножества, в которых находятся числа, делящиеся на 5. Про остальные числа можно сказать, что они не делятся на 5. Получается 2 подмножества N, они не пересекаются, и их объединение – все мн-во N. При помощи 1-го св-ва мн-во разбивается на 2 класса: 1кл – обладает св-вом; 2кл – не обладает св-вом. Рассмотрим случай, когда для элементов мн-ва заданы 2 св-ва: 1 – «быть кратным 5» 2 – «быть кратным 3» В результате можно выделить 2 подмножества А – кратны 5 В – кратны 3 Множества А и В пересекаются, и в пересечении находятся числа, которые кратны 15, то для того, чтобы выделение данных свойств привело к разбиению на классы, необходимо выделить следующие подмножества: 1) – кратны 5, но не 3 2) – кратны 3, но не 5 3) – кратны и 3 и 5 4) – не кратны 3 и 5 Выделение 2-х св-в привело в разбиению на 4 класса. Рассмотрим 2 свойства натуральных чисел: 1 – быть кратным 3 2 – быть кратным 6 А – кратны 3 В – кратны 6 1)кратны 6 2) кратны 3, но не 6 3) не кратны 3 Выделение 2-х св-в привело к разбиению на 3кл. Множества, состоящие из чисел, называют числовыми множествами. N – множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество действительных чисел. Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.
4.Определение. Пересечением множеств А и В называется множество, содержащее элементы, принадлежащие и множеству А и множеству В одновременно. Пересечение обозначают: А∩ В. Таким образом, по определению, А ∩ В = { х | х∈Аих∈В}. Например, если А = { a, c, k, m, n } и В = { a, b, c, d, e }, то А ∩ В = { a, c }. Для пересечения множеств выполняются следующие свойства. •коммутативность: А ∩ В = В ∩ А •ассоциативность: (А ∩ В) ∩ С = А ∩ (В ∩ С) •А ∩ ∅ = ∅ •А ∩ А = А 5.Определение. Объединением множеств А и В называется множество, содержащее элементы, принадлежащие хотя бы одному из множеств. Объединение обозначают: А∪В. Таким образом, по определению, А∪В = { х | х∈А или х∈В}. Например, если А = { a, c, k, m, n } и В = { a, b, c, d, e }, то А∪В = { a, c, k, m, n, b, d, e }. Для объединения множеств выполняются следующие свойства: · Коммутативность: А ∪В = В∪А. · Ассоциативность: (А ∪В)∪С = А∪ (В∪С). · А ∪∅= А. · А ∪А = U. 6.Определение. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В. Разность обозначают А \ В. Таким образом, по определению разности А \ В = { х | х∈Аих∉В}. Например, если А = { a, c, k, m, n } и В = { a, b, c, d, e }, то А \ В = { k, m, n }. Определение. Пусть В подмножество А. В этом случае разность множеств А и В называют дополнением подмножества В до множества А и обозначают В'. Разность множеств и дополнение к подмножеству обладают рядом свойств: · (А \ В) \ С = (А \ С) \ В. · (А∪В) \ С = (А \ С) ∪ (В \ С). · (А \ В) ∩ С = (А ∩С) \ (В ∩ С). · А \ (В ∪ С) = (А \ В)∩(А \ С). · А \ (В ∩ С) = (А \ В) ∪ (А \ С). 7.Определение. Декартовым произведением множеств А и В называется множество, состоящее из пар, первая компонента которой принадлежит А, а вторая компонента принадлежит В. Декартово произведение обозначается: АxВ. Определение. Парой чисел а и б называется упорядоченное множество (а;в), где а – первая компонента пары и в- вторая компонента пары. Свойства декартово произведения множеств: · Не обладает коммутативностью · Дистрибутивность декартово произведения относительно объединения множеств · Дистрибутивность декартово произведения относительно разности множеств. Определение. Кортежем длины n называют упорядоченный набор из элементов. Кортеж записывается: n= (а1; а2; а3; …; аn) 9.Определение. Высказывание - повествовательное предложение, относительно которого имеет смысл говорить истинно оно или ложно. Логическими значениями высказываний являются «истина» и «ложь». Различают два вида высказываний: ü Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. ü Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если.... то...», «тогда и только тогда», принято называть сложными или составными. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным. Примеры высказываний: · Москва стоит на Неве. (ложно –Л; простое) · Лондон — столица Англии. (истинно – И; простое) · Сокол не рыба.(истинно – И; сложное) · Число 6 делится на 2 и на 3.(истинно – И; сложное) Логические операции над высказываниями: Ø Отрицание. Определение. Отрицанием высказыванияА называется новое высказывание, которое является истинным, если высказывание х ложно. Ø Конъюнкция. Определение. Конъюнкцией двух высказываний X и Y называется новое высказывание, которое считается истинным только тогда, когда оба высказывания истинны. Ø Дизъюнкция. Определение. Дизъюнкцией двух высказываний А и В называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний истинно, и ложным, если они оба ложны. Ø Импликация. Определение. Импликацией двух высказываний А и В называется новое высказывание, которое считается ложным только тогда, когда из истины следует ложь. Ø Эквивалентность. Определение. Эквивалентностью двух высказыванийА и В называется новое высказывание, которое считается истинным, когда оба высказывания принимают одинаковые значения. 29.Правило суммы: Если а можно выбрать х способами, а б у способами, то выбор элемента «а или б» можно осуществить х+у способами. Имеются 4 желтых и 3 красных воздушных шарика. Сколькими способами можно выбрать один шарик. Ж-4 кр-3 = 7 выбор одного шарика (либо, либо) можно осуществить 4+3 способами. Правило произведения: Если а можно выбрать х способами, а б у способами, то элемент «а и б» можно выбрать х*у сп. Имеются 5 красных, 4 желтых, 4 розовых шарика. Сколькими способами можно составить букет из 3 роз разного цвета. Кр-5 ж-4 р-4) 5*4*4=80 Сколько 2х значных чисел можно составить из цифр 7,4,1 при условии 1. Цифры могут повторяться. (3*3=9) 2. Не могут повторяться (3*2=6) Сколько 4х значных цифр можно составить из 0,8 (1*2*2*2=8) 34. О. т.з. – есть описание на естественном языке нек.явления, ситуации или процесса с требованием дать кол-ную характеристику к-л компонента этого явления, установить наличие или отсутствие отношений между компонентами или определить вид этого отношения. Структура т.з.- любая т.з.представляет собой описание к-л явления, ситуации и процесса. С этой точки зрения т.з. является словесной моделью некоторого явления. Как и в любой модели в текстовых задачах опис.не все явления в целом, а лишь некоторые его стороны, в основном кол-ные характеристики. Типы т.з. по отнош.между условиями и требованиями. 1. Определенные (в них заданных условий столько, сколько необходимо и достаточно для выполнения требования) 2. Недоопределенные (в них условий недостаточно для выполнения требований) 3. Переопределенные (в них есть лишние условия) Этапы решения. и у алгебраического и у арифметического. 1. Восприятие и анализ содержания задачи. 2. Поиск и составления плана решения задачи. 3. Выполнение плана решения. Формулировка вывода о выполнении требования задачи (ответа на вопрос задачи). 4. Проверка решения и устранение ошибок, если они есть. Формулировка окончательного вывода о выполнении требования задачи или ответа на вопрос задачи. Основная цель первого этапа решения – понимание решающим в целом ситуации, описанной в задаче, понимание условий задачи, ее требования или вопроса, смысла всех терминов и знаков, имеющихся в тексте. 35. О. т.з. – есть описание на естественном языке нек.явления, ситуации или процесса с требованием дать кол-ную характеристику к-л компонента этого явления, установить наличие или отсутствие отношений между компонентами или определить вид этого отношения. Основные методы решения – арифметический и алгебраический. О. решить задачу арифм.методом – значит найти ответ на требование задачи при помощи выполнения арифметических действий над числами. (можно решать несколькими способами, они будут отличаться логикой рассуждения). Пример. Сшили 3 платья, расходуя на каждое по 4 метра ткани. Сколько кофт можно сшить из этой ткани, если расходовать на 1 кофту по 2 м. 1. 4*3=12 2. 12:2=6. 1. 4:2=2 2. 3*2=6 О. решить задачу алгебраическим методом – значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений. (тоже можно несколькими способами) Пример. Свитер, шапку и шарф связали из 1кг 200г шерсти, шарф на 100 гр больше шапки и на 400 гр меньше свитера. Сколько шерсти израсх.на каждую вещь? Пусть х-это шарф. Х-(х-100) + (х+400)=1200 3х+300=1200 3х=900 Х=300гр. И т.д. Моделирование при решении текстовых задач. Примеры моделей. О. мат.модель-это описание к-л реального процесса на языке мат.понятий. формул и отношений. Мат.моделью текст.зад.явл.выражение,если з.решается арифметическим методом, и уравнение, если алгебраическим. Этапа мат.моделирования. 1. Перевод условий на мат.язык(выд.необходимые для решения данные и искомые и матем. Способами описывают связи между ними) 2. Внутримодельное решение (решение уравнения или нахождение значения выражения) 3. Интерпритация (перевод полученного решения на язык, на котором была сформулирована исходная задача) Чтобы облегчить 1 этап строят вспомогательные модели. Процесс решения задачи- переход от словесной к вспомогательной модели, а от нее к математической. Виды моделей. 1. Знаковые (должны быть представлены все её объекты, все отношения между ними, указаны требования) Естеств.язык - краткая запись и таблицы. Матем.язык – выражения,уравнения, запись по действиям. Схематизированные Выщ-ные – обеспечивают физическое действие с предметами (спички, пуговицы) Графические – исп.для обобщенного схематического создания ситуации, описанной в задаче (рисунок (обыч.условн.) чертеж(обычн.схематич.)). БИЛЕТ 36. ПОНЯТИЕ АЛГОРИТМА. СВОЙСТВА АЛГОРИТМА. ВИДЫ АЛГОРИТМОВ. СПОСОБЫ ОПИСАНИЯ АЛГОРИТМОВ Алгоритмом называется точное и понятное предписаниe исполнителю совершить последовательность действий, направленных на решение поставленной задачи. Слово «алгоритм» происходит от имени математика Аль Хорезми, который сформулировал правила выполнения арифметических действий. Первоначально под алгоритмом понимали только правила выполнения четырех арифметических действий над числами. В дальнейшем это понятие стали использовать вообще для обозначения последовательности действий, приводящих к решению любой поставленной задачи. Говоря об алгоритме вычислительного процесса, необходимо понимать, что объектами, к которым применялся алгоритм, являются данные. Алгоритм решения вычислительной задачи представляет собой совокупность правил преобразования исходных данных в результатные. Основными свойствами алгоритма являются: 1.детерминированность (определенность). Предполагает получение однозначного результата вычислительного процecca при заданных исходных данных. Благодаря этому свойству процесс выполнения алгоритма носит механический характер; 2.результативность. Указывает на наличие таких исходных данных, для которых реализуемый по заданному алгоритму вычислительный процесс должен через конечное число шагов остановиться и выдать искомый результат; 3.массовость. Это свойство предполагает, что алгоритм должен быть пригоден для решения всех задач данного типа; 4.дискретность. Означает расчлененность определяемого алгоритмом вычислительного процесса на отдельные этапы, возможность выполнения которых исполнителем (компьютером) не вызывает сомнений. Алгоритм должен быть формализован по некоторым правилам посредством конкретных изобразительных средств. К ним относятся следующие способы записи алгоритмов: словесный, формульно-словесный, графический, язык операторных схем, алгоритмический язык.
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |

 наборов.
наборов.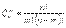

 получаем: наборов.
получаем: наборов. получаем: наборов.
получаем: наборов. получаем: способов.
получаем: способов. получаем способов.
получаем способов.



