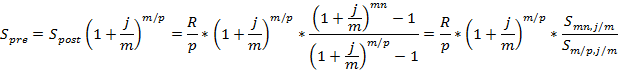Денежные потоки и методы их оценки

В большинстве современных коммерческих отношениях подразумеваются не разовые платежи, а последовательность денежных поступлений или выплат, в течение определенного периода. Например: серия выплат задолженностей, регулярные и нерегулярные взносы в различные фонды, получение и погашение долгосрочного кредита и др. Такая последовательность называется потоком платежей. Оценка потока платежей может решать две задачи:

1. Прямая – оценка с позиций будущего или наращение.

2. Обратная – с позиций настоящего (дисконтирования).

Поток однонаправленных платежей с равными интервалами между последовательными платежами в течение определенного времени называется аннуитетом, или финансовой рентой. Например: регулярные взносы в пенсионный фонд.

Аннуитет является частным случаем денежного потока (anno – в переводе с латинского «год»). Различают следующие виды аннуитетов:

1. По величине размеров платежей:

- постоянные аннуитеты;

- непостоянные аннуитеты.

2. По количеству платежей:

- ограниченные;

- бесконечные.

3. По моментам выплат:

- пренумерандо (Pre);

- постнумерандо (Post).

Аннуитет, для которого платежи осуществляются в начале соответствующих интервалов, носит название аннуитета пренумерандо (авансовый аннуитет). Если платежи осуществляются в конце интервалов, то аннуитет носит название постнумерандо или обычный аннуитет. Аннуитеты, в которых платежи равны между собой либо изменяются в соответствии с определенной закономерностью, называются постоянными аннуитетами.

Приняты к использованию следующие обозначения:

S – наращенная величина аннуитета, т.е. сумма всех платежей с начисленными процентами;

Spre – наращенная величина аннуитета пренумерандо;

Spost – наращенная величина аннуитета постнумерандо;

A – приведенная (дисконтированная) величина аннуитета, т.е. сумма всех платежей с процентами в будущем, приведенная к настоящему времени;

Apre – приведенная величина аннуитета пренумерандо;

Apost – приведенная величина аннуитета постнумерандо;

R – годовая величина отдельного платежа;

i (j) – годовая ставка сложных процентов, в долях;

n – срок ренты, в годах;

p – количество выплат по аннуитету в течение года;

m – количество начисленных процентов в течение года;

K_i,n (S_m,j) – множитель наращения с параметрами i,n или m,j; характеризует будущую стоимость срочного аннуитета в одну денежную единицу продолжительности n (m) периодов;

a_i,n – множитель приведения аннуитета, дисконтирующий множитель с параметрами i,n; характеризует приведенную стоимость срочного аннуитета в одну денежную единицу продолжительностью n периодов. Составлены таблицы для определения множителей приведения и наращения для различных значений i и n.

Будущая стоимость аннуитета постнумерандо

Будущая стоимость аннуитета постнумерандо определяется по формуле

Возможны следующие частные случаи:

а) поступления по аннуитету 1 раз в год (p=1), начисление сложных процентов m раз в год:

б) рента p-срочная, m=1, т.е. рента выплачивается p раз в год равными платежами, проценты начисляются 1 раз в конце (m=1):

в) рента p-срочная, m=p, т.е. число выплат ренты в году совпадает с количеством начислений процентов:

г) рента p-срочная, m≠p, т.е. число выплат ренты в году не совпадает с количеством начислений процентов:

 

Расчет приведенной (дисконтированной) величины аннуитета постнумерандо

Если поступления по аннуитету 1 раз в год (p=1), начисления сложных процентов 1 раз в год (m=1), то приведенная стоимость аннуитета постнумерандо рассчитывается по формуле

Возможны следующие частные случаи:

а) поступления по аннуитету 1 раз в год (p=1), начисление сложных процентов m раз в год:

б) рента p-срочная, m=1, т.е. рента выплачивается p раз в год равными платежами, проценты начисляются 1 раз в конце года (m=1):

в) рента p-срочная, m=p, т.е. число выплат ренты в году совпадает с количеством начислений процентов:

г) рента p-срочная, m≠p, т.е. число выплат ренты в году не совпадает с количеством начислений процентов:

 

Будущая стоимость аннуитета пренумерандо

Для нахождения размера платежа и срока аннуитета пренумерандо можно найти для заданных значений величины S_pre и A_pre и пользоваться формулами для аннуитета постнумерандо.

Возможны следующие частные случаи:

а) поступление аннуитета один раз в год, начисление процентов m раз в год:

б) рента p-срочная, m=1:

в) рента p-срочная, m=p:

 

г) рента p-срочная, m≠p: