
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы, принимающие значение «истина» при всех наборах значений входящих в нее переменных, называются тождественно истинными или тавтологиями.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одна из задач математической логики состоит в поиске формул, являющихся тавтологиями и противоречиями (тождественно ложными, т.е. принимающими при всех наборах значений переменных значение «ложь»). Способы рассуждений, формализующиеся тавтологиями, затем применяются при доказательстве утверждений. 2. Определим порядок выполнения операций: 1) отрицание
Заполняем первый столбик значениями истинности переменной А, для этого число пустых строк делим пополам (8: 2 = 4) и в половине пишем значение «истина», а в оставшейся половине – «ложь»:
Заполняем второй столбик значениями истинности переменной В. Для этого число пустых строк делим на 4 (8: 4 = 2) и попеременно записываем в строки по одному значению «истина» и «ложь» таким образом, чтобы каждому значению истинности переменной А соответствовали по два значения истинности переменной В:
Заполняем третий столбик значениями истинности переменной С. Для этого число пустых строк делим на 8 (8: 8 = 1) и попеременно записываем в строки по одному значению «истина» и «ложь» таким образом, чтобы каждому значению истинности переменной В соответствовали оба значения истинности переменной С:
Заполняем четвертый столбик результатами выполнения операции отрицания
Аналогичным образом заполняем пятый столбик результатами операции отрицания
В шестом столбике записываем результаты выполнения операции дизъюнкции
И, наконец, в седьмом столбике записываем результат выполнения итоговой операции эквиваленции
Вывод следующий: истинность высказывания, имеющего данную логическую структуру, зависит от значений истинности составляющих его элементарных высказываний. Формулы такого вида (принимающие при некоторых наборах переменных значение «истина», а при некоторых – значение «ложь») называются выполнимыми (опровержимыми).
С помощью таблиц истинности можно установить, при каких наборах значений истинности входящих переменных формула будет принимать истинное или ложное значение (а также высказывание, имеющее соответствующую логическую структуру), какие формулы будут тавтологиями или противоречиями, а также установить, являются ли две данные формулы равносильными. В логике говорят, что два предложения равносильны, если они одновременно истинны, либо одновременно ложны. Слово «одновременно» в этой фразе неоднозначно. Так, для предложений «Завтра будет вторник» и «Вчера было воскресенье» это слово имеет буквальный смысл: в понедельник они оба истинны, а в остальные дни недели – оба ложны. Для уравнений «х = 2» и «2х = 4» «одновременно» означает «при одних и тех же значениях переменной». Прогнозы «Завтра будет дождь» и «Неверно, что завтра не будет дождя» одновременно подтвердятся (окажутся истинными) либо не подтвердятся (окажутся ложными). В сущности, это один и тот же прогноз, выраженный в двух разных формах, которые можно представить формулами Х и
Видим, что значения истинности в первом и последнем столбцах совпадают. Такие формулы, как и соответствующие им предложения, естественно считать равносильными. Формулы F1 и F2 называются равносильными, если их эквиваленция Равносильность двух формул записывается так: Проверить, равносильны ли формулы, можно двумя способами: 1) составить их эквиваленцию и с помощью таблицы истинности проверить, не является ли она тавтологией; 2) для каждой формулы составить таблицу истинности и сравнить итоговые результаты; если в итоговых столбцах при одинаковых наборах значений переменных значения истинности обеих формул будут равны, то формулы являются равносильными. Пример. Выяснить, являются ли формулы равносильными: Равносильности формул логики высказываний часто называют законами логики. Перечислим наиболее важные из них: I. II. III. IV. V. VI. VI. VII. VIII Законы логики используются для упрощения сложных формул и для доказательства тождественной истинности или ложности формул.
Контрольные вопросы:
1. Дайте определение высказывания и высказывательной формы. 2. Перечислите основные логические связки. 3. Дайте определение логической операции. 4. Дайте определение негации, конъюнкции, дизъюнкции, импликации и эквиваленции. 5. Какие переменные называются пропозициональными? 6. Сформулируйте определение формулы логики высказываний. 7. Опишите процедуру формализации высказываний. 8. Для чего нужна таблица истинности? 9. Опишите алгоритм составления таблицы истинности. 10. Какие формулы называются тавтологиями, противоречиями, выполнимыми (опровержимыми)? 11. Какие формулы называются равносильными? 12. Сформулируйте несколько основных законов логики. 13. Для чего нужны законы логики?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 777; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.185.51 (0.01 с.) |

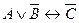 . Данная формула содержит 3 различные переменные и 4 символа логических операций. Число строк в таблице – 23 + 1 = 8 + 1 = 9. Число столбцов – 3 + 4 = 7.
. Данная формула содержит 3 различные переменные и 4 символа логических операций. Число строк в таблице – 23 + 1 = 8 + 1 = 9. Число столбцов – 3 + 4 = 7.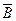 ; 2) отрицание
; 2) отрицание  ; 3) дизъюнкция
; 3) дизъюнкция 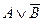 и 4) эквиваленция
и 4) эквиваленция 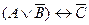 . Нарисуем таблицу и заполним строку заголовка, начиная с элементарных формул:
. Нарисуем таблицу и заполним строку заголовка, начиная с элементарных формул: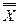 . Эти формулы одновременно принимают значение «истина» либо значение «ложь». Для проверки достаточно составить таблицу истинности:
. Эти формулы одновременно принимают значение «истина» либо значение «ложь». Для проверки достаточно составить таблицу истинности:
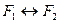 – тавтология.
– тавтология. (читается: формула F1 равносильна формуле F2).
(читается: формула F1 равносильна формуле F2). - закон тождества (утверждает, что мысль, заключенная в некотором высказывании, остается (считается) неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует).
- закон тождества (утверждает, что мысль, заключенная в некотором высказывании, остается (считается) неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует).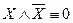 - закон противоречия (никакое предложение не может быть истинным одновременно со своим отрицанием).
- закон противоречия (никакое предложение не может быть истинным одновременно со своим отрицанием).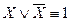 - закон исключенного третьего (закон альтернативы).
- закон исключенного третьего (закон альтернативы).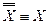 - закон двойного отрицания.
- закон двойного отрицания. ;
; 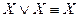 - законы тождества (или идемпотентности (на латинском языке «idem» означает «то же», а «potentia» - «сила»)).
- законы тождества (или идемпотентности (на латинском языке «idem» означает «то же», а «potentia» - «сила»)).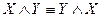 ;
; 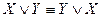 - законы коммутативности (переместительности).
- законы коммутативности (переместительности). ;
; 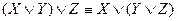 - законы ассоциативности (сочетательности).
- законы ассоциативности (сочетательности).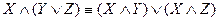 ;
; 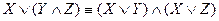 - законы дистрибутивности (распределительности).
- законы дистрибутивности (распределительности). ;
; 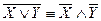 - законы де Моргана (английский логик, 1806-1871).
- законы де Моргана (английский логик, 1806-1871).


