Возникновение логики. Основные характеристики аристотелевской логики.

ПРЕДМЕТ И ЗНАЧЕНИЕ ЛОГИКИ

 

Для выяснения предмета логики можно использовать несколько методов, каждый из которых дает определенный результат.

Первый метод – этимологический. Он заключается в том, что требуется прояснить значение слова, которое используется для названия данной науки. Термин «логика» восходит к древнегреческому слову «логос», означавшему слово, мысль, понятие, рассуждение и закон. Древнегреческие философы считали, что в речах человека есть некая сила. Она побуждает, сказав «А», сказать и «Б». В основе этого принуждения лежит человеческий разум, который отыскивает в природе необходимое и отбрасывает случайное.

Этимология слова «логика» показывает, что это наука, имеющая отношение к человеческому мышлению, обосновывает рассуждения с помощью оснований, которые впоследствии стали называться логическими законами.

Недостатком данного метода является многозначность слова «логика». В повседневной жизни, в популярной, общенаучной и философской литературе это слово используется в большом спектре значений. Оценки «логично» и «нелогично» могут использоваться для характеристики человеческих действий, оценки событий и т. п.

Второй метод – справочно-академический. Он заключается в том, что ответ на вопрос мы ищем в словарях и энциклопедиях. В большинстве словарей и учебников логика определяется как наука о законах и формах правильного мышления, а предметом данной науки признается человеческое мышление. Однако логика рассматривает не только правильное мышление, но и ошибки, возникающие в процессе мышления: софизмы, парадоксы и т. д.

Логика – наука о законах и формах человеческого мышления, рассматриваемого как средство познания окружающей действительности.

Значение логики состоит в следующем:

1) логика выступает важнейшим средством формирования убеждений (прежде всего научных). Эти убеждения опираются на доказательные процедуры своего представления и обоснования. Именно в этом плане логика применялась даже средневековыми схоластами, пытавшимися придать христианскому вероучению рациональную форму, что послужило формальной предпосылкой возникновения действительной науки, отказавшейся от теологических подходов;

2) формальная логика применяется в науке и технике. При этом техническими приложениями формальной логики являются: исчисление высказываний и исчисление предикатов. Без исчисления предикатов не могли появиться искусственные информационные языки, основа современной компьютерной техники. Традиционная формальная логика остается важнейшим логическим инструментом построения доказательств, обоснований во всех науках;

3) традиционная формальная логика остается важнейшим средством в сфере всех видов образования. Она является основой организации всех видов знания для его подачи в процессе обучения;

4) логика является важнейшим и незаменимым инструментом развития культуры. Без логики не может обойтись никакая культурная деятельность вообще, поскольку в ней присутствуют и играют принципиальную роль рациональные элементы.

Предметом логики выступает дискурсивное мышление. Оно позволяет найденным смыслам обрести строгие формы. Оно не хаотично, а движется в русле заранее заданных правил. Поэтому дисциплинированное дискурсивное мышление можно назвать формальным. Для Аристотеля понятие «форма» выступает выражением идеальной сущности вещи. Логику называют теорией правильных рассуждений.

 

Логика и естествознание: индуктивная логика Ф.Бэкона.

индуктивная логика

раздел логики, изучающий индуктивные умозаключения, которые отличаются от дедуктивных умозаключений тем, что вывод в них вытекает из посылок не с необходимостью, а лишь с некоторой вероятностью. Типичным примером индуктивного умозаключения является переход от единичных фактов к общему утверждению

ИНДУКТИВНАЯ ЛОГИКА — раздел логики, в котором изучается индукция. Индукция как познавательная процедура, приводящая к обобщению в результате обнаружения сходства наблюдаемых предметов, в современной логике может быть формализована различными средствами, образуя соответствующие варианты индуктивной логики. Вариант формализации индукции, предложенный Р. Карнапом, основан на интерпретации вероятности как логического отношения между двумя высказывания. Это отношение выражает степень подтверждения гипотезы h эмпирическими данными е, обычно понимаемыми как констатация результатов наблюдений. Р. Карнап отличает понятие логической вероятности от эмпирической вероятности, изучаемой в теории вероятностей и математической статистике. Он использует язык логика предикатов первого порядка и “описания состояний” (модели), с помощью которых он вводит числовую функцию меры от, областью значений которой является закрытый числовой промежуток между 0 и 1. Сумма значений от-функции на “описаниях состояния” равна 1; от-функция логически ложных высказываний равна 0, а от-функция логически истинных высказываний равна 1. Высказывания, не являющиеся ни логически истинными, ни логически ложными, имеют значение от-функции, заключенное между 0 и 1. Степень подтверждения гипотезы h данными наблюдения е определяется как отношение значения от-функции для конъюнкции h не к значению от-функции для е.

 

Метод познания. Указывая на плачевное состояние науки, Бэкон говорил, что до сих пор открытия делались случайно, не методически. Их было бы гораздо больше, если бы исследователи были вооружены правильным методом. Метод — это путь, главное средство исследования. Даже хромой, идущий по дороге, обгонит нормального человека, бегущего по бездорожью.

Исследовательский метод, разработанный Фрэнсисом Бэконом — ранний предшественник научного метода. Метод был предложен в сочинении Бэкона «Novum Organum» («Новый Органон») и был предназначен для замены методов, которые были предложены в сочинении «Organum» («Органон») Аристотеля почти 2 тысячелетия назад.

В основе научного познания, согласно Бэкону, должны лежать индукция и эксперимент.

Индукция может быть полной (совершенной) и неполной. Полная индукция означает регулярную повторяемость и исчерпаемость какого-либо свойства предмета в рассматриваемом опыте. Индуктивные обобщения исходят из предположения, что именно так будет обстоять дело во всех сходных случаях. В этом саду вся сирень белая — вывод из ежегодных наблюдений в период её цветения.

Неполная индукция включает обобщения, сделанные на основе исследования не всех случаев, а только некоторых (заключение по аналогии), потому что, как правило, число всех случаев практически необозримо, а теоретически доказать их бесконечное число невозможно: все лебеди белы для нас достоверно, пока не увидим чёрную особь. Это заключение всегда носит вероятностный характер.

Пытаясь создать «истинную индукцию», Бэкон искал не только факты, подтверждающие определенный вывод, но и факты, опровергающие его. Он, таким образом, вооружил естествознание двумя средствами исследования: перечислением и исключением. Причем главное значение имеют именно исключения. С помощью своего метода он, например, установил, что «формой» теплоты является движение мельчайших частиц тела.

Итак, в своей теории познания Бэкон неукоснительно проводил мысль о том, что истинное знание вытекает из чувственного опыта. Такая философская позиция называется эмпиризмом. Бэкон и был не только его основоположником, но и самым последовательным эмпириком.

Понятие и слово. Образование понятий.

Понятие является одной из форм абстрактного мышления. Конкретные предметы и их св-ва отражают с помощью форм чувств, познания – ощущения, восприятие, представление. В понятие отражается лишь существенные признаки. Признаки – предметы сходные друг с другом или наоборот. Св-ва и отношения являются признаками. Представления могут быть тождественными (сахар, мед) по св-вам (мед сладки, лимон кислый). Признаки бывают существенные и несущественные. Понятия – форма мышления в ктр отражаются существенные признаки класса однородных предметов. Языковыми формами выражения понятий являются словосочетания или слова (книга, спорт кар). Основными лог приемами формирования понятий явл: Анализ, синтез, сравнения, обобщения, абстрагирование.

Синтез – мысленное соединение в ед целое частей предмета, полученных в процессе анализа. Анализ – расчленение предметов на их составные части, мысленное выделение в них признаков. Сравнение – мысленное установление сходства или различия предметов по существенным или не существенным признакам. Абстрагирование – мысленное выделение одних признаков предмета и отвлечение от других. Обобщение – мысленное объединение отдельных предметов в нектр понятие.

Понятие как и имя выражается в языке словом или словосочетанием, но если имя лишь указывает на предмет, то понятие раскрывает его сущность.

 

Виды понятий.

В практике мышления функционирует множество определенных и разнообразных понятий. Они подразделяются на виды в соответствии с двумя фундаментальными логическими характеристиками любого понятия – содержанием и объемом.

Объективные различия между предметом мысли отражаются в различиях между понятиями прежде всего по их содержанию. В соответствии с этим признаком понятия делятся на следующие наиболее значимые группы.

Конкретные – понятия, в которых находят свое отражение сами предметы и явления, обладающие относительной самостоятельностью существования (книга, ручка).

Абстрактные – это понятия, в которых мыслятся свойства предметов или отношения между предметами, не существующие самостоятельно без этих предметов (жесткость, электропроводимость).

Необходимо учитывать, что если абстрактное понятие, отражающее свойство, употребляется применительно к самим предметам, обладающим этим свойством, то они обретают множественное число.

Те понятия, в которых отражается наличие у предметов мысли каких-либо качеств, свойств и так далее, называются положительными.

Отрицательные понятия – это понятия, характеризующиеся отсутствием у предметов мысли каких-либо качеств, свойств и т. п. Для выражения отрицательных понятий используются отрицательные частицы («не») и отрицательные приставки («без-» и «бес-»). Кроме русских, могут быть использованы иностранные отрицательные приставки («а-», «анти-», «дез-», «контр-» и др.

Также понятия делятся на соотносительные и безотносительные.

В соотносительных понятиях один предмет мысли предполагает существование другого и без него невозможен – соотносится с ним («родители» и «дети»: нельзя быть сыном или дочерью без родителей).

В безотносительных понятиях мыслится предмет, существующий до известной степени самостоятельно – отдельно от других: «природа», «человек» и т. д.

Собирательные и несобирательные понятия различаются в зависимости от того, как соотносится с охватываемыми ими предметами мысль: с группой предметов в целом или с каждым предметом этой группы в отдельности. Одна из особенностей собирательных понятий состоит в том, что они не могут быть отнесены к каждому предмету одного класса.

Особенность несобирательных понятий заключается в том, что они относятся не только к группе предметов в целом, но и к каждому отдельному предмету данной группы.

Пустые понятия – они относятся к реально не существующим предметам или явлениям («русалка», «леший», «идеальный газ»).

Непустые понятия относятся к реальным предметам («город», «космическое тело»).

Единичные понятия – объем понятия, составляющий один предмет («Солнце», «Россия»).

Общие понятия – отражают в своем объеме группу предметов («звезда», «планета»).

Деление понятий на виды по их содержанию и объему позволяет в огромном понятийном материале выделить наиболее крупные и распространенные группы, а также более или менее отчетливо представлять себе особенности этих групп.

Единичное понятие – такое, в объем которого входит один элемент (город Саратов, Россия и др.).

Общее понятие – такое, в объем которого входит более одного элемента (студент, солдат, преступник и др.).

 

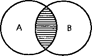
Отношения между понятиями.

Понятия, объемы которых полностью или частично совпадают, называются совместимыми. Существуют три вида отношений совместимости: 1) равнообьемность, 2) пересечение и 3) подчинение (субординация).

1. В отношении равнообъемности находятся понятия, в которых мыслится один и тот же предмет. Объемы этих понятий полностью совпадают (хотя содержание различно). В отношении равнообъем­ности находятся, например, понятия «геометрическая фигура с тремя равными углами» и «геометрическая фигура с тремя равными сторонами».

Отношение между понятиями принято изображать с помощью круговых схем (кругов Эйлера), где каждый круг обозначает объем понятия, а каждая его точка — предмет, мыслимый в его объеме.

2. В отношении пересечения (перекрещивания) находятся поня­тия, объем одного из которых частично входит в объем другого. Содержание этих понятий различно.

В отношении пересечения находятся понятия «юрист» (А) и «преподаватель» (В): некоторые юристы являются преподавателя­ми (как некоторые преподаватели — юристами).

3. В отношении подчинения (субординации) находятся понятия, объем одного из которых полностью входит в объем другого, состав­ляя его часть.

В таком отношении находятся, например, понятия «суд» (А) и «городской суд» (В). Объем первого понятия шире объема второго понятия, кроме городских существуют и другие виды судов — крае­вые, областные, районные и т.д. Понятие «городской суд» полнос­тью входит в объем понятия «суд».

Несовместимые понятия

Понятия, объемы которых не совпадают ни полностью, ни час­тично, называются несовместимыми (или внеположными). Эти понятия содержат признаки, исключающие совпадение их объ­емов.

Существуют три вида отношений несовместимости: соподчине­ние (координация), 2) противоположность, 3) про­тиворечие (контрадикторность).

1. В отношении соподчинения (координации) находятся два или больше неперекрещивающихся понятий, подчиненных общему для них понятию. Например: «областной суд» (В), «городской суд» (С), «суд» (А). Понятия, находящиеся в отношении подчинения к обще­му для них понятию, называются соподчиненными.

2. В отношении противоположности (контрарности) находятся понятия, одно из которых содержит некоторые признаки, а дру­гое — признаки, не совместимые с ними. Такие понятия называются противоположными (контрарными). Объемы двух противополож­ных понятий составляют в своей сумме лишь часть объема общего для них родового понятия, видами которого они являются и которо­му они соподчинены; Таковы, например, отношения между поня­тиями «черный» и «белый», «отличник» и «неуспевающий», «друже­ственное государство» и «враждебное государство».

3. В отношении противоречия (контрадикторности) находятся понятия, одно из которых содержит некоторые признаки, а другое эти же признаки исключает.

В отношении противоречия находятся положительные и отрица­тельные понятия: «четный» и «нечетный», «успевающий» и «неуспе­вающий», «дружественное государство» и «недружественное госу­дарство».

Лог. опер. над понятиями наз. действие над этой формой мышления, в некоторой степени измен. её, с целью достижения какой-либо цели, результата.

 

Деление понятий и его виды.

Еще одной важной операцией является деление понятий.

Деление некоторого непустого понятия aВ(a) – это переход от данного понятия к некоторой системе непустых понятий S = {aА1(a), aА2(a), …, aАn(a)}, каждое из которых является видовым по отношению к исходному. В состав деления входят:

1) Делимое понятие – родовое понятие aВ(a), объем которого разбивается на классы.

2) Члены деления – видовые понятия aА1(a), aА2(a), …, aАn(a), полученные в результате такого разбиения.

3) Основание деления – характеристика предметов, входящих в объем делимого понятия, модификация которой и порождает систему членов деления S.

Сущность деления состоит в том, что предметы, входящие в объем делимого понятия, распределяются по группам.

Операция деления позволяет правильно распределить предметы по группам, изучить их, а следовательно, глубже познать весь класс в целом.

В зависимости от выбранного основания деления, различают следующие виды деления: дихотомическое и по видоизменению основания.

В случае дихотомического деления родового понятия aВ(a) основанием деления является признак, присущий лишь части предметов, входящих в объем aВ(a). Деление осуществляется по наличию или отсутствию этого признака у предметов делимого понятия.

При делении по видоизменению основания в качестве основания деления используются варьируемые характеристики элементов объема делимого понятия (вес, цвет, объем, форма, величина и т.п.).

 

Простые суждения и их виды.

Простым называется суждение, не включающее другие сужде­ния..

Атрибутивным (от латинского attributio — «свойство», «при­знак») называется суждение о признаке предмета. В нем отражает­ся связь между предметом и его признаком, эта связь утверждается или отрицается. Атрибутивные суждения называют также категорическими (от греческого kategorikos — «ясный», «безусловный», «не допускаю­щий иных толкований»).

Атрибутивное, или категорическое, суждение состоит из субъек­та, предиката и связки; его логическая схема S—Р, где S — субъект суждения, Р — предикат суждения, «—» — связка.

Субъектом суждения называется понятие о предмете суждения. Понятие о признаке предмета называется предикатом суждения. Связка выражает отношение между субъектом и предикатом.

Поэтому основную смысловую нагрузку несет предикат.

Атрибутивному суждению может быть дана объемная интерпре­тация. В этом случае оно рассматривается не как связь между пред­метом и его признаком, а как включение объема одного понятия в объем другого или исключение из него.

Реляционные суждения – раскрывают наличие или отсутствие у предмета мысли того или иного отношения к другому предмету.

Экзистенциальные суждения – раскрывают наличие или отсутствие предмета мысли.

 

Сложные суждения и их виды.

Сложным называют суждение, состоящее из нескольких про­стых, связанных логическими связками. Различают следующие виды сложных суждений: 1) соединительные, 2) разделительные, 3) услов­ные, 4) эквивалентные. Истинность таких сложных суждений опре­деляется истинностью составляющих их простых.

1. Соединительные (конъюнктивные) суждения.

Соединительным, или конъюнктивным называют суждение, со­стоящее из нескольких простых, связанных логической связкой «и». Например, суждение «Кража и мошенничество относятся к умыш­ленным преступлениям» является соединительным суждением, со­стоящим из двух простых: «Кража относится к умышленным преступлениям», «Мошенничество, относится к умышленным преступ­лениям». В естественном языке конъюнктивная связка может быть пред­ставлена и такими выражениями, как: «а», «но», «а также», «как и», «хотя», «однако», «несмотря на», «одновременно» и другими.

Соединительное суждение может быть как двух-, так и многосо­ставным; в символической записи: р л q л г л... л п.

2. Разделительные (дизъюнктивные) суждения.

Разделительным, или дизъюнктивным, называют суждение, со­стоящее из нескольких простых, связанных логической связкой «или». Например, суждение «Договор купли-продажи может быть заключен в устной или письменной форме» является разделитель­ным суждением, состоящим из двух простых: «Договор купли-прода­жи может быть заключен в устной форме»; «Договор купли-продажи может быть заключен в письменной форме». Разделительное суждение может быть как двух-, так и многосо­ставным: р v q v... v п.

3. Условные (импликативные) суждения.

Условным, или импликативным, называют суждение, состоя­щее из двух простых, связанных логической связкой «если.., то...». Например: «Если предохранитель плавится, то электролампа гас­нет». Первое суждение — «Предохранитель плавится» называют ан­тецедентом (предшествующим), второе — «Электролампа гас­нет» —консеквентом (последующим).

4. Эквивалентные суждения (двойная импликация). Эквивалентным называют суждение, включающее в качестве составных два суждения, связанных двойной (прямой и обратной) условной зависимостью, выражаемой логической связкой «если и только если—, то...». Например: «Если и только если человек на­гражден орденами и медалями (р), то он имеет право на ношение соответствующих орденских планок (q)».

Логическая характеристика этого суждения состоит в том, что истинность утверждения о награждении (р) рассматривается как необходимое и достаточное условие истинности утверждения о на­личии права на ношение орденских планок (q). Точно так же истин­ность утверждения о наличии права на ношение орденских планок (q) является необходимым и достаточным условием истинности ут­верждения о том, что данное лицо награждено соответствующими орденом или медалью (р). Такую обоюдную зависимость символи­чески можно выразить двойной импликацией p(Стрелочка влево и стрелочка вправо)q, которая читает­ся: «Если и только если р, то q». Эквивалентность выражают и другим знаком: р = q(Вместо 2х линий 3).

 

Основные законы логики.

Неумышленное нарушение законов логики называется паралогизмом.
1. Закон тождества. В процессе рассуждения любая мысль должна быть тождественной самой себе. Оставаться неизменной и не подменяться другой (нарушением этого закона является известный рогатый софизм).
Нельзя отождествлять различное и разнотождествлять тождественное.

Закон тождества- всякая мысль в процессе рассуждения должна быть тождественна сама себе, т.е. нельзя отождествлять различные мысли (подмена понятий) и тождеств. мысли пренемать за нетождеств.. Лог. формула: p→p. Из зак. следует,что нельзя отождествю. различные мысли и тождеств. принимать за нетождеств.. «Иванов совершил кражу=Иванов тайно похитил чужую вещь» P этих сужд.-равнозначные понятия, а S вообще один и тот же.

Но не надо отождествлять различные мысли. Остерегайтесь подмены понятий.

Этот зак. особо важен для юристов, ему нужно неукоснительно следовать в процессе работы. Точность в понятиях наиболее важна, их необходимо употреб. в нужном значение, т.к. ошибка может привести к трагическим последствиям. При разбарательстве дела необходимо выяснить точный смысл каждого понятия.
2. Закон не противоречия.
Невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении (Аристотель).
"Молодая была немолода"
"Не бываемое бывает"

Закон не противоречия- два несовместимых друг с другом суждения не могут быть одновременно истинными, хотя бы одно из них ложно. Лог. формула не(p и не p), не p- любое высказывание, искл. p. Зак. действ. в отнош. всех несовместных (не могут быть одновремен. ист., но могут быть лож.) сужд.. Т.е. должно быть единство признака, пердмета обсуждения, времени, отношения (места, по сравнеию с др. и т.д.).

3. Закон исключенного третьего. Два противоречащих суждения могут находиться лишь в двух отношениях: истина или ложь, другого не дано.
Если закон не противоречия запрещает одновременно принимать истину и ложь, то закон исключенного третьего запрещает их одновременно отвергать.

Закон искл. третьего- два противоречащих (не могут быть одновремен. ни ист., ни лож.) сужд. не могут бытть одновременно ложными, одно из них необходимо истинно. Лог. формула: a есть либо b, либо не b. (Все коошки ночью яв. серыми= некотор. кошки ночью не яв. серыми).
4. Закон достаточного основания. Любое суждение должно иметь крепкий фундамент, который состоит из имеющихся фактов или из других суждений.
В любом рассуждении для каждого производного суждения должны быть предъявлены основания, позволяющие считать его истинным или ложным.
Истинное суждение не должно ссылаться само на себя и само себя подтверждать. Закон требует ответа на вопрос "почему"?

Закон достаточного основания- всякая мысль признаётся ист., если она имеет достаточное основание. Аргументация утверждения. a→b.

Достаточным основ. может быть личный опыт чел., научные достижения, весь опыт человечества, аксиомы (зак., не треб. доказ.), лю.бая др. достоверная мысль. Истинность сужд. уст. путём их сравнеия с фактами действительности: улиакми, свид. показ., др. имеющемися фактами. Но достаточ. основ. не могут служит ьразличные догмы, предрассутки и суеверия. нужно опиратся только на достоверные факты.

Вынесение мотивированного приговора или решения суда яв. главным принципом судопроизводства во всех демокр. странах. Не стоит принемать необоснованных решений.

 

Метод остатков

Применение метода связано с установлением причины, вызы­вающей определенную часть сложного действия при условии, что причины, вызывающие другие части этого действия, уже выявле­ны.

Схема рассуждения по методу остатков имеет следующий вид:

1) АВС вызывает xyz

2) А вызывает х

3) В вызывает у

С вызывает z

Схема модифицированного рассуждения по методу остатков имеет следующий вид:

1) АВС вызывает abed

2) А вызывает а

3) В вызывает Ь

4) С вызывает с

По-видимому, существует некий X, который вызывает d

Подобно другим индуктивным выводам метод остатков дает, как правило, проблематичное знание. Степень вероятности заключения в таком выводе определяется, во-первых, точностью знаний о пред­шествующих обстоятельствах, среди которых идет поиск причины исследуемого явления, во-вторых, точностью знания о степени вли­яния каждой из известных причин на совокупный результат. При­близительный и неточный перечень предшествующих обстоя­тельств, как и неточное представление о влиянии каждой из извест­ных причин на совокупное действие, может привести к тому, что в заключении вывода в качестве неизвестной причины будет пред­ставлено не необходимое, а лишь сопутствующее обстоятельство.

49.Умозаключение по аналогии, их структура и виды. Аналогия и моделирование.

Аналогия – это умозаключение о принадлежности предмету определенного признака на основе сходства в признаках с другим предметом.

Аналогия дает не строго достоверные, а правдоподобные выводы. Поэтому, чтобы не получить ложных результатов, ею нужно пользоваться осторожно.

Существуют следующие правила «правильного пользования» аналогией:

1) нужно установить как можно больше сходных признаков у сравниваемых предметов;

2) найти у сравниваемых предметов существенные с точки зрения рассматриваемого вопроса признаки;

3) стремиться к тому, чтобы признаки сравниваемых предметов были специфическими;

4) необходимо учитывать количество и существенность пунктов различия;

5) переносимый признак должен быть того же типа, что и сходные.

Различают два вида аналогии: аналогию предметов и аналогию отношений.

Аналогия предметов. В данном умозаключении объектом уподобления выступают два единичных предмета, события или явления, а переносимым признаком являются свойства этих предметов.

Аналогия отношений – это умозаключение, в котором объектом уподобления выступают отношения между двумя парами предметов, а переносимым признаком являются свойства этих отношений.

Также выделяют аналогию строгую, нестрогую и ложную. Строгая аналогия применяется в научных исследованиях, в математических доказательствах. На основах умозаключения по строгой аналогии основан метод моделирования. Научные аналогии позволяют использовать имеющийся к настоящему времени опыт, при этом, кроме формально логических принципов проведения аналогии, необходимо учитывать и методологические требования конкретной истины, рассмотрения явлений в конкретно-исторической обстановке.

Нестрогая аналогия дает не достоверное, а вероятное заключение. Например, испытание прочности моста на модели, затем построение настоящего моста.

При нарушении правил применения аналогии аналогия может дать ложное заключение, т. е. стать ложной. Вероятность заключения по ложной аналогии равна нулю.

Рассмотренные три вида аналогии делятся в зависимости от характера выводного знания, т. е. по степени достоверности заключения: получено истинное заключение, определенная степень вероятности заключения или ложное заключение. Вероятные заключения тем ценнее, чем их вероятность ближе к истине.

В процессе познания место аналогии предопределяется ее логической природой как умозаключение от единичного к единичному.

При выяснении причин возникновения или свойств единичных предметов и событий обращаются не только к законам и научным обобщениям, но и к ранее приобретенным знаниям о сходных явлениях. Отсюда и возникает необходимость использования умозаключения по аналогии.

Судья и следователь, анализируя фактический материал, используют не только знания, полученные наукой и практикой, но также они обращаются к знаниям, полученным в результате опыта – как своего, так и чужого.

Умозаключение по аналогии в своем большинстве используется при производстве некоторых криминалистических экспертиз в результате идентификации личности или материальных предметов.

 

Виды доказательств.

В науке и практике в зависимости от области исследования пользуются различными способами доказательства гипотез. Основными среди них являются три способа: дедуктивное обоснование выраженного в гипотезе предположения; логическое доказательство гипотезы; непосредственное обнаружение предположенных в гипотезе предметов.
Применительно к судебному исследованию имеются два основных способа превращения версий в достоверное знание: (1) непосредственное обнаружение искомых предметов и (2) логическое доказывание версий путем подтверждения следствий.
Логическое доказывание гипотезы в зависимости от способа обоснования может протекать в форме косвенного или прямого доказывания. Косвенное доказывание протекает путем опровержения и исключения всех ложных версий, на основании чего утверждают достоверность единственного оставшегося предположения.
Заключение в этом выводе может расцениваться как достоверное, если, во-первых, построен исчерпывающий ряд версий, объясняющих исследуемое событие, и, во-вторых, в процессе проверки версий опровергнуты все ложные предположения. Версия, указывающая на оставшуюся причину, в этом случае будет единственной, а выраженное в ней знание будет выступать уже не как проблематичное, а как достоверное.
Этот способ доказывания, протекающий по методу исключения, часто используется в судебно-следственной практике при доказывании как общих, так и частных версий.
Косвенное доказывание гипотез при расследовании преступлений должно применяться с учетом особенностей этого вида исследования.
Прежде всего следует отметить практическую трудность построения в отдельных случаях полного перечня версий, объясняющих исследуемое событие. При явной недостаточности исходного материала в начале расследования трудно бывает точно и определенно перечислить все реально возможные причины, которые объясняли бы происхождение фактических данных.

 

Требования к аргументации, типичные логические ошибки.

Логичное рассуждение предполагает соблюдение двух правил в отношении тезиса: определенность тезиса и неизменность тезиса.

(1) Определенность тезиса

Правило определенности означает, что тезис должен быть сфор­мулирован ясно и четко.

(2) Неизменность тезиса

Правило неизменности тезиса запрещает видоизменять или отступать от первоначально сформулированного положения в процессе данного рассуждения.

Требование логической точности, определенности и неизменнос­ти тезиса достаточно просты и, как правило, выполняются при нали­чии элементарных навыков логической культуры. Однако в практи­ке встречаются отступления от этих правил.

Первое из них — потеря тезиса.

Потеря тезиса проявляется в том, что, сформулировав тезис, про­понент забывает его и переходит к иному, прямо или косвенно свя­занному с первым, но в принципе другому положению. Затем, часто по ассоциации, он затрагивает третье положние, а от него переходит к сходному четвертому и т.д. В конце концов он теряет исходную мысль. Подмена тезиса. Общее название ошибки по отношению к тези­су — подмена тезиса, которая бывает полной или частичной.

(1) Полная подмена тезиса проявляется в том, что, выдвинув определенное положение, пропонент в итоге фактически обосновы­вает нечто другое, близкое или сходное с тезисом положение и тем самым подменяет основную идею другой.

(2) Частичная подмена тезиса выражается в том, что в ходе выступления пропонент пытается видоизменить собственный тезис, сужая или смягчая свое первоначально слишком общее, преувели­ченное либо излишне резкое утверждение. Так, первоначальное ут­верждение о том, что «все участники преступления действовали умышленно», видоизменяется до утверждения «большинство из них...», затем до утверждения «отдельные...» и т.д.

2. Правила и ошибки по отношению к аргументам

Решение стратегической задачи аргументации определяется вы­полнением следующих требований, или правил в отношении до­водов:

(1) достоверность аргументов;

(2) автономное от тезиса обоснование;

(3) непротиворечивость;

(4) достаточность.

(1) Требование достоверности, т.е. истинности и доказаннос­ти аргументов определяется тем, что они выступают логическими основаниями, опираясь на которые выводят тезис. Сколь бы вероят­ными ни были доводы, из них может следовать лишь правдоподоб­ный, но не достоверный тезис.

Доводы выполняют роль фундамента, на котором строится аргументация.

Нарушение указанного логического правила приводит к двум ошибкам. Одна из них — принятие за истину ложного аргумен­та — называется «основное заблуждение».

Причины такой ошибки — использование в качестве аргумента несуществующего факта, ссылка на событие, которое в действитель­ности не имело места, указание на несуществующих очевидцев и т.п.

Другая ошибка — «предвосхищение основания». Она заключается в том, что в качестве аргументов исполь­зуются недоказанные, как правило, произвольно взятые положения.

(2) Автономное обоснование аргументов означает: поскольку доводы должны быть истинными, то, прежде чем обосновывать тезис, следует проверить сами аргументы. При этом для доводов изыскивают основания, не обращаясь к тезису. Иначе может полу­читься, что недоказанным тезисом обосновываются недоказанные аргументы. Эта ошибка называется «круг в демонстрации».

(3) Требование непротиворечивости аргументов вытекает из ло­гической идеи, согласно которой из противоречия формально следу­ет все что угодно — и тезис пропонента, и антитезис оппонента. Содержательно же из противоречивых оснований с необходимостью не вытекает ни одно положение.

(4) Требование достаточности аргументов связано с логичес­кой мерой — в своей совокупности доводы должны быть такими, чтобы из них по правилам логики в необходимости следовал доказы­ваемый тезис.

Логическая состоятельность и доказательное значение рассуждения во многом зависит от качества исходного фактического и теоретического материала - убеждающей силы аргументов.

Процесс аргументации всегда предполагает предварительный анализ имеющегося фактического и теоретического материала, статистических обобщений, свидетельств оче