
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление числовой информацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Информация Количество информации Количеством информации называют ее числовую характеристику, отражающую ту степень неопределенности, которая исчезает после получения информации. Для оценки и измерения количества информации в сообщении применяются различные подходы, среди которых следует выделить статистический и алфавитный. Статистический подход. Для количественной оценки неопределенности или энтропии Н Хартли Р. предложил формулу, содержащую логарифм от числа равновероятных возможностей N H = log 2 N, (1) которую можно записать в следующем виде: 2 H = N, (2) где H – количество информации. Минимальной единицей количества информации, именуемой битом, будет выбор из двух возможностей. При не равновероятной возможности выбора количество информации hi, зависящей от индивидуальной вероятности Pi i – го выбора, вычисляется по формуле К. Шеннона
которую можно преобразовать к виду
Удобнее в качестве меры количества информации пользоваться не значнем hi, а средним значением количества информации
Алфавитный подход позволяет определить количество текстовой информации. Количество информации, которое несёт каждый символ вычисляется по формуле i = log 2 N, (6) где N – мощность алфавита, равная количеству символов в нём. Текст, содержащий K символов, имеет объём информации, равный I = K · i. (7) Максимальное количество слов L из m букв, которое можно составить с помощью алфавита мощностью N, определяется как L = N m. (8)
Примеры решения задач с равновероятными возможностями
П 1.1. Пусть имеется колода карт, содержащая 32 различные карты. При выборе одной карты имеется 32 возможности. Решение: Число возможностей N = 32 при подстановке в формулу (1) дает количество информации H = 5 (2 H = 25). П 1.2. При бросании монеты выбор одного результата (например, выпадения орла) несет один бит информации, поскольку количество возможных равновероятных результатов N = 2 (орел или решка). Действительно, подставляя N = 2 в формулу (1), получим H = 1 бит. П 1.3. Какой объем информации содержит сообщение, уменьшающее неопределенность в 4 раза? Решение: так как неопределенность знаний уменьшается в 4 раза, следовательно, она была равна 4, т.е. существовало 4 равновероятных события. Сообщение о том, что произошло одно из них, несет 2 бита информации (4 = 22). Ответ: 2 бита. П 1.4. В коробке лежат 16 кубиков. Все кубики разного цвета. Сколько информации несет сообщение о том, что из коробки достали красный кубик? Решение: из 16 равновероятных событий нужно выбрать одно. Поэтому N = 16, следовательно, H = 4, (16 = 24). Пояснение: события равновероятны, т.к. всех цветов в коробке присутствует по одному. Ответ: 4 бита. П 1.5. Сообщение о том, что ваш друг живет на 10 этаже, несет 4 бита информации. Сколько этажей в этом доме? Решение: N = 24 = 16 этажей. Пояснение: события равновероятны, т.к. номера этажей не повторяются. Ответ: 16 этажей.
Примеры решения задач с не равновероятными событиями
П 1.6. В корзине лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар? Дано: N ч = 8; N б = 24. Найти: H ч =? Решение: 1) N = 8 + 24 = 32 – шара всего; 2) Pч = 8/32 = ¼ - вероятность доставания черного шара; 3) H = log 2 (1/ ¼) = 2 бита. Ответ: 2 бита. П 1.7. В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в коробке? Дано: N ч = 64; H б = 4. Найти: К б =? Решение: 1) H б = log 2(1/ P б); 4 = log 2(1/ P б); 1/ P б = 16; P б = 1/16 – вероятность доставания белого карандаша; 2) P б = К б/ N; 1/16 = К б/64; К б = 64/16 = 4 белых карандаша. Ответ: 4 белых карандаша. П 1.8. В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего шаров в корзине? Дано: К ч = 16, N = 2 бита. Найти: N -? Решение: 1) 1/ P б = 21, 1/ P б = 22 = 4, P б = ¼ - вероятность доставания белого шара; 2) P б = К б/ N = К б/(К б + К ч), ¼ = К б/(К б + 18), К б + 18 = 4 * К б, 18 = 3 * К б, К б = 6 – белых шаров; 3) N = К б + К ч = 18 + 6 = 24 шара было в корзине. Ответ: 24 шара лежало в корзине.
Примеры решения задач на измерение алфавитного объёма
П 1.9. Найти объем текста HT, записанного на языке, алфавит которого содержит N = 128 символов и K = 2000 символов в сообщении. Решение: 1) H = log 2 N = log 2128 =7 бит – объем одного символа. 2) HT = H × K = 7 × 2000 = 14 000 бит – объем сообщения. Ответ: 14 000 бит. П 1.10. В алфавите некоторого языка всего N = 2 буквы, каждое слово в языке состоит точно из m = 7 букв. Какой максимальный запас слов в языке? а) 128; б) 256; в) 64; г) 1024. Решение: Если мощность алфавита N, а максимальное количество букв в слове, записанном с помощью этого алфавита, – m, то максимально возможное количество слов определяется по формуле L = Nm, откуда N = 27, следовательно, N = 128.
Тестовые задачи
Т 1.1. «Вы выходите на следующей остановке?» - спросили человека в автобусе. «Нет», - ответил он. Сколько информации содержит ответ? Варианты ответа: а) 1 бит; б) 2 бита; в) 3 бита; г) 4 бита. Т 1.2. Сколько информации содержит сообщение, уменьшающее неопределенность знаний в 8 раз? Варианты ответа: а) 1 бит; б) 2 бита; в) 3 бита; г) 4 бита. Т 1.3. При угадывании целого числа в некотором диапазоне было получено 8 бит информации. Сколько чисел содержит этот диапазон? Варианты ответа: а) 128; б) 256; в) 64; г) 32. Т 1.4. В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже 8 полок. Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации библиотекарь передал Пете? Варианты ответа: а) 5 бит; б) 6 бит; в) 7 бит; г) 8 бит. Т 1.5. При угадывании целого числа в диапазоне от 1 до N было получено 9 бит информации. Чему равно N? Варианты ответа: а) 64; б) 128; в) 256; г) 512. Т 1.6. В группе N = 30 студентов. За контрольную работу по математике получено К 5 = 15 пятерок, К 4 = 6 четверок, К 3 = 8 троек и К 2 = 1 двойка. Какое количество информации Н 5 в сообщении о том, что Андреев получил пятерку? Варианты ответа: а) 1 бит; б) 2 бита; в) 3 бита; г) 4 бита. Т 1.7. За семестр студент получил N = 100 оценок. Сообщение о том, что он получил пятерку, несет Н 5 =2 бита информации. Сколько пятерок К 5 студент получил за четверть? Варианты ответа: а) 15; б) 20; в) 25; г) 30. Т 1.8. В ящике лежат перчатки (белые и черные). Среди них – Кч = 2 пары черных. Сообщение о том, что из ящика достали пару черных перчаток, несет Нч = 4 бита информации. Сколько пар белых перчаток Кб было в ящике? Варианты ответа: а) 20; б) 30; в) 40; г) 48. Т 1.9. Для ремонта актового зала использовали белую, синюю и коричневую краски. Израсходовали одинаковое количество банок белой и синей краски Кб = Кс. Сообщение о том, что закончилась банка белой краски, несет Нб = 2 бита информации. Синей краски израсходовали Кс = 8 банок. Сколько банок коричневой краски Кк израсходовали на ремонт актового? Варианты ответа: а) 8; б) 12; в) 16; г) 20. Т 1.10. На остановке останавливаются троллейбусы с разными номерами. Сообщение о том, что к остановке подошел троллейбус с номером N1, несет НN1 = 4 бита информации. Вероятность появления на остановке троллейбуса с номером N2 в два раза меньше, чем вероятность появления троллейбуса с номером N1 (РN1 = 2РN2). Сколько информации НN2 несет сообщение о появлении на остановке троллейбуса с номером N2? Варианты ответа: а) 5 бит; б) 6 бит; в) 7 бит; г) 8 бит. Т 1.11. В корзине лежат 32 клубка шерсти. Среди них – 4 красных. Сколько информации несет сообщение о том, что достали клубок красной шерсти? Варианты ответа: а) 1 бит; б) 2 бита; в) 3 бита; г) 4 бита. Т 1.12. В корзине лежат красные и зеленые шары. Среди них 15 красных шаров. Сообщение о том, что из корзины достали зеленый шар, несет 2 бита информации. Сколько всего в корзине шаров? Варианты ответа: а) 18; б) 20; в) 22; г) 24. Т 1.13. Известно, что в ящике лежат N = 20 шаров. Из них – Кс = 10 синих, Кз = 5 – зеленых, Кж = 4 – желтых и Кк = 1 – красный. Какое количество информации несут сообщения о том, что из ящика случайным образом достали черный шар Нч, белый шар Нб, желтый шар Нж, красный шар Нк? Варианты ответа: а) Нч = 1 бит, Нб = 2 бита, Нж = 2,236 бит, Нк = 4,47 бит. б) Нч = 2 бита, Нб = 4 бита, Нж = 2, 6 бит, Нк = 4,47 бит. в) Нч = 1 бит, Нб = 2 бита, Нж = 3 бита, Нк = 4 бита. г) Нч = 3 бита, Нб = 2 бита, Нж = 2,236 бит, Нк = 4,47 бит. Т 1.14. В корзине находятся всего 128 красных, синих и белых шаров, причем красных шаров в три раза больше, чем синих. Сообщение о том, что достали белый шар, содержит 3 бита информации. Найти количество синих шаров. арианты ответа: а) 24;) 28; в) 32; г) 36. Т 1.15. В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Сколько информации мы получим, когда поймаем какую-нибудь рыбу? Варианты ответа: а) 1, 5 бит; б) 1, 75 бит; в) 2 бита; г) 2, 25 бит. Т 1.16. Сообщение, записанное буквами из 64-х символьного алфавита, содержит 20 символов. Какой объем информации оно несет? Варианты ответа: а) 100 бит; б) 110 бит; в) 120 бит; г) 130 бит. Т 1.17. Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение? Варианты ответа: а) 8; б) 16; в) 24; г) 32. Т 1.18. Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации содержат 5 страниц текста? Варианты ответа: а) 850 байт; б) 950 байт; в) 1050 байт; г) 1150 байт. Т 1.19. В алфавите некоторого языка всего две буквы: «А» и «Б». Все слова, записанные на этом языке, состоят из 11 букв. Какой максимальный словарный запас может быть у этого языка? Варианты ответа: а) 22; б) 11; в) 2048; г) 1024; д) 44. Т 1.20. Словарный запас некоторого языка составляет 256 слов, каждое из которых состоит точно из 4 букв. Сколько букв в алфавите языка? Варианты ответа: а) 8; б) 4; в) 64; г) 1024; д) 256. Системы исчисления Система счисления – это способ представления чисел и соответствующие ему правила действия с числами. Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами. В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы: I V L C D M 1 5 10 50 100 500 1000 П 1.11. Число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно 232. В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются, например: VI = 5 + 1 = 6, а IV = 5 – 1 = 4. П 1.12. Записать римское число MCMXCVIII в десятичной системе MCMXCVIII = 1000 + (- 100 + 1000) + (-10 +100) + 5 + 1 + 1+ 1 = 1998. В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием позиционной системы счисления. Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Позиционный характер этой системы легко понять на примере любого многозначного числа. Например, в числе 333 первая тройка означает три сотни, вторая – три десятка, третья – три единицы. Для записи чисел в позиционной системе с основанием n нужно иметь алфавит из n цифр. Обычно для этого при n < 10 используют n первых арабских цифр, а при n > 10 к десяти арабским цифрам добавляют буквы. Вот примеры алфавитов нескольких систем:
Если требуется указать основание системы, к которой относится число, то оно приписывается нижним индексом к этому числу. Например: 1011012, 36718, 3В8F16. В системе счисления с основанием q (q -ичная система счисления) единицами разрядов служат последовательные степени числа q. q единиц какого-либо разряда образуют единицу следующего разряда. Для записи числа в q -ичной системе счисления требуется q различных знаков (цифр), изображающих числа 0, 1, …, q – 1. Запись числа q в q -ичной системе счисления имеет вид 10. Развернутой формой записи числа называется запись в виде
Здесь Aq –само число, q – основание системы счисления, ai – цифры данной системы счисления, n – число разрядов целой части числа, m – число разрядов дробной части числа. Свернутой формой записи числа называется запись в виде
которой пользуются в повседневной жизни. П 1.13. Записать в развернутом виде число А10 = 4718,63 А10 = 4*103 + 7*102 + 1*101 + 8*100 + 6*10-1 + 3*10-2. П 1.14. Записать в развернутом виде число А8 = 7764,1 А8 = 7*83 + 7*82 + 6*81 + 4*80 + 1*8-1. П 1.15. Записать в развернутом виде число А16 = 3АF А16 = 3*163 + 10*161 + 15*160. П 1.16. Все числа 1123, 1011012, 15FC16, 101,112 перевести в десятичную систему 1123 = 1*32 + 1*31 + 2*30 = 9 + 3 + 2 = 1410, 1011012 = 1*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 32 + 8 + 4 + 1 = 4510, 15FC16 = 1*163 + 5*162 + 15*161 + 12 = 4096 + 1280 + 240 + 12 = 562810, 101,112 = 1*22 + 0*21 + 1*20 + 1*2-1 + 1*2-2 = 4 + 1 + ½ + ¼ = 5 + 0,5 + 0, 25 = 5,7510. П 1.17. У жителей села «Не десятичное» на ферме имеется 120 голов рогатого скота, из них 53 коровы и 34 быка. Какая система счисления используется сельчанами? Решение: Самая большая цифра в рассматриваемых числах – это цифра 5. Значит, она входит в состав алфавита искомой системы счисления. Тогда основание системы счисления больше 5. Задачу можно решить методом подстановки оснований 6 и 7 или математически. Примем за х основание искомой системы счисления. Тогда после перевода чисел, стоящих в правой и левой частях, в десятичную систему счисления получим следующее равенство: х 2 + 2 х = 5 х + 3 + 3 х + 4. После преобразований получим уравнение х 2 – 6 х – 7 = 0. Ответ х = 7. Тестовые задачи
Т 1.21. В саду 100 q плодовых кустарников, из них 33 куста малины, 22 куста смородины красной, 16 кустов черной смородины и 17 кустов крыжовника. В какой системе счисления подсчитаны деревья? Варианты ответа: а) 7; б) 9; в) 11; г) 13. Т 1.22. Было 53 q груши. После того, как каждую из них разрезали пополам, стало 136 половинок. В системе счисления с каким основанием вели счет? Варианты ответа: а) 11; б) 13; в) 15; г) 17. Т 1.23. Какое число больше? Варианты ответа: а) 1527; б) 15210; в) 15212; г) 15216. Т 1.24. Переведите двоичные числа в восьмеричную систему счисления: а) 110000110101; 1010101 б) 11100001011001; 1000010101. Т 1.25. Переведите двоичные числа в шестнадцатеричную систему счисления: а) 11011010001; 111111111000001 б) 10001111010; 100011111011. Т 1.26. Переведите шестнадцатеричные числа в двоичную систему счисления: а) 1АС7 б) FACC. Т 1.27. Переведите числа из восьмеричной системы счисления в шестнадцатеричную: а) 774; б) 665.
Тестовые задачи Т 1.28. Выбрать фрагмент текста, имеющий минимальную сумму кодов в таблице ASCII. Варианты ответа: а) 2b2d; б) файл; в) file; г) 1999; д) 2001. Т 1.29. Какое минимальное количество бит потребуется для кодирования 26 прописных и строчных латинских букв. Варианты ответа: а) 5 бит; б) 6 бит; в) 7 бит; г) 8 бит. Т 1.30. В каком порядке будут идти фрагменты текста «excel», «байт», «8в», «10г», «9а», «10а», если упорядочить их по убыванию? Варианты ответа: а) байт, excel, 8в, 9а, 10г, 10а; б) байт, excel, 8в, 9а, 10а, 10г; в) 10а, 10г, 9а, 8в, байт, excel; г) байт, excel, 10г, 10а, 9а, 8в; д) excel, байт, 10г, 10а, 9а, 8в. Т 1.31. Во сколько раз увеличиться информационный объем страницы текста при его преобразовании из кодировки Windows 1251 (таблица кодировки содержит 256 символов) в кодировку Unicode (таблица кодировки содержит 65536 символов)? Варианты ответа: а) 2; б) 4; в) 6; г) 8.
Тестовые задачи Т 1.32. Какой объем видеопамяти необходим для хранения двух страниц изображения при условии, что разрешающая способность дисплея равна 640×350 пикселей, а количество используемых цветов – 16? Варианты ответа: а) 54,3 Кбайт; б) 124,3 Кбайт; в) 174,4 Кбайт; г) 218,7 Кбайт. Т 1.33. Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея – 800×600 пикселей? Варианты ответа: а) 4,8 Мбайт; б) 5,5 Мбайт; в) 6,7 Мбайт; г) 7,2 Мбайт. Т 1.34. Объем видеопамяти равен 1 Мбайт. Разрешающая способность дисплея – 800×600. Какое максимальное количество цветов можно использовать при условии, что видеопамять делится на две страницы? Варианты ответа: а) 64; б) 128; в) 256; г) 512. Т 1.35. Битовая глубина равна 32, видеопамять делится на две страницы, разрешающая способность дисплея – 800×600. Вычислить объем видеопамяти. Варианты ответа: а) 3,7 Мбайт; б) 4,8 Мбайт; в) 5,5 Мбайт; г) 6,4 Мбайт. Т 1.36. Видеопамять имеет объем, в котором может храниться 4-х цветное изображение размером 640×480. Какого размера изображение можно хранить в том же объеме видеопамяти, если использовать 256-цветную палитру? Варианты ответа: а) 160×120; б) 320×240; в) 640×480; г) 800×600. Т 1.37. На экране монитора необходимо получить 1024 оттенка серого цвета. Какой должна быть глубина цвета? Варианты ответа: а) 10 бит; б) 20 бит; в) 30 бит; г) 40 бит. Т 1.38. Объем видеопамяти – 2 Мбайта, разрешающая способность дисплея равна 800×600. Сколько оттенков серого цвета можно получить на экране при условии, что видеопамять делится на две страницы? Варианты ответа: а) 512; б) 1024; в) 1536; г) 2048. Ответ: 1024 оттенка. Т 1.39. Объем видеопамяти равен 2,5 Мбайта, глубина цвета – 16, разрешающая способность экрана монитора – 640×480 точек. Найти максимальное количество страниц, которое можно использовать при этих условиях. Варианты ответа: а) 2; б) 3; в) 4; г) 5. Т 1.40. Видеопамять имеет объем, в котором может хранится 8-цветное изображение размером 640×350 точек. Какого размера изображение можно хранить в том же объеме видеопамяти, если использовать 512-цветную плитру? Варианты ответа: а) 151245; б) 182434; в) 253624; г) 273066. Т 1.41. После преобразования графического изображения количество цветов увеличилось с 256 до 65536. Во сколько раз увеличился объем занимаемой памяти? Варианты ответа: а) 3,5; б) 2,5; в) 1,5; г) 0,5. Т 1.42. Растровый графический редактор предназначен для: а) создания чертежей; в) построения диаграмм; б) построения графиков; г) создания и редактирования рисунков. Т 1.43. Из предложенного списка графическими форматами является: 1) TIFF; 2) TXT; 3) MPI; 4) JPG; 5) BMP. Верные утверждения содержатся в варианте ответа: а) 2, 3, 5; б) 1, 4, 5; в) 4, 5; г) 1, 2. Т 1.44. Энтропия в информатике – это свойство: а) данных; б) знаний; в) информации; г) условий поиска. Т 1.45. Семантический аспект информации: а) определяет информацию с точки зрения ее практической полезности для получателя; б) определяет отношения между единицами информации; в) определяет значение символа естественного алфавита; г) дает возможность раскрыть ее содержание и показать отношение между смысловыми значениями ее элементов. Т 1.46. СMYK является: а) графическим редактором; б) системой представления цвета; в) форматом графических файлов; г) типом монитора. Т 1.47. Если 1110 = 23х, то основание системы счисления Х равно: а) 4; б) 8; в) 10; г) 16.82. Т 1.48. Словарный запас некоторого языка составляет 256 слов, каждое из которых состоит точно из 4 букв. Сколько букв в алфавите языка? а) 8; б) 4; в) 64; г) 1024; д) 256. Тестовые задачи Т 2.1. Установите хронологическую последовательность изобретения перечисленных приспособлений для счета: а) аналитическая машина Ч. Беббиджа; б) арифмометр «Паскалина»; в) абак; г) счеты. Т 2.2. Первым программистом считается: а) Готфрид Лейбниц; б) Ада Лавлейс; в) Джон фон Нейман; г) Блез Паскаль. Т 2.3. Продолжите фразу: «Деление электронной вычислительной техники на поколения обусловлено…» а) исторической обстановкой; б) развитием элементной базы; в) уменьшением размеров компьютеров; г) развитием науки. Т 2.4. Установите соответствие между поколениями ЭВМ и основными составляющими элементной базы. К каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
Запишите в таблицу выбранные буквы, а затем получившуюся последовательность букв без пробелов и других символов запишите в ответ.
Тестовые задачи Т 2.5. В левой части таблицы приведены названия носителей, а в правой – их возможная емкость. К каждой позиции левого столбца подберите соответствующую позицию из правого столбца.
Запишите в таблицу выбранные буквы, а затем получившуюся последовательность букв без пробелов и других символов запишите в ответ. Т 2.6. Что из перечисленного является носителем информации? 1. дистрибутив; 2. флоппи-диск; 3. блокнот; 4. пластинка; 5. дисковод. Выберите правильный вариант ответа: а) 2, 3, 4, 5; б) 2, 3, 4; в) 1, 2, 5; г) 1, 2, 4, 5. Т 2.7. Что из перечисленного входит в состав системы НЖМД? 1. головки записи / чтения; 2. гибкий диск; 3. дисковод; 4. жесткий диск. Выберите правильный вариант ответа: а) 1, 2, 3; б) 1, 2, 4; в) 1, 2, 3; г) 1, 2, 4. Т 2.8. К какому типу памяти относится жесткий диск персонального компьютера? а) внутренняя; б) внешняя; в) центральная; г) переносная. Т 2.9. Теоретические основы функционирования и структуры ЭВМ разработаны группой ученых под руководством: а) Джона фон Неймана; б) Билла Гейтса; в) Эмиля Поста; г) Алана Тьюринга. Т 2.10. Во время исполнения прикладная программа хранится: а) в видеопамяти; б) в процессоре; в) в оперативной памяти; г) в ПЗУ. Т 2.11. При отключении компьютера информация стирается: а) из оперативной памяти; б) из постоянного запоминающего устройства; в) на магнитном диске; г) на компакт-диске.
2.3. Устройства ввода (вывода) С этой темой можно ознакомиться в разделе 2.3. пособия [1].
Тестовые задачи
Т 2.12. Установите соответствие между периферийными устройствами компьютера и их разновидностью в классификации. К каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
Запишите в таблицу выбранные буквы, а затем получившуюся последовательность букв без пробелов и других символов запишите в ответ. Т 2.13. Какое из перечисленных устройств вывода можно использовать для ввода информации? а) монитор с сенсорным экраном; б) принтер – копир; в) плоттер; г) звуковые колонки. Тестовые задачи
Т 3.1. Выберите операционную систему: а) Adobe; б) IBM PC; в) API; г) UNIX. Т 3.2. Редактирование текста представляет собой: а) процесс внесения изменений в имеющийся текст; б) процедуру сохранения текста на диске в виде текстового файла; в) процесс передачи текстовой информации по компьютерной сети; г) процедуру считывания с внешнего запоминающего устройства ранее созданного текста. Т 3.3. Задан полный путь к файлу C:\KOD\MOD\text.doc. Каково содержимое корневого каталога диска С: а) MOD; б) KOD; в) KOD\MOD; г) text.doc. Т 3.4. В основные функции операционной системы не входит: а) организация файловой структуры; б) обеспечение диалога с пользователем; в) разработка программ для ЭВМ; г) управление ресурсами компьютера. Т 3.5. Для управления файлами и папками в ОС Windows можно использовать: а) панель управления; б) проводник; в) меню кнопки «Пуск»; г) панель задач. Т 3.6. В текстовом редакторе при задании параметров страницы устанавливаются: а) гарнитура, размер, начертание; б) отступ, интервал; в) поля, ориентация; г) стиль, шаблон. Т 3.7. Установите соответствие между приложениями, перечисленными в первом столбце, и их назначением во втором столбце таблицы.
Выберите правильный ответ. а) г в а б; б) в г б а; в) в г а б; г) б г а в. Т 3.8. Из предложенного списка файлов: 1).doc; 2).gif; 3).jpg; 4).exe; 5).bmp; 6).bak, выберите расширения графических файлов: а) 1,3,5; б) 2,3,4; в) 2,3,5; г) 3,5,6. Основы логики Тестовые задачи Составить и записать сложные высказывания из простых с использованием логических операций. Т 4.1. Неверно, что Варианты ответа: а) в) Т 4.2. Z является min (Z, Х, Y). Варианты ответа: а) (Z < Y)Λ(Z < X); б) (Z > Y)Λ(Z < X); в) (Z < Y)V(Z < X); г) (Z < Y)Λ(Z > X). Т 4.3. А является max (A, B, C). Варианты ответа: а) (A > B) Λ (A < C); б) (A > B) Λ (A > C); в) (A < B) Λ (A > C); г) (A > B) V (A > C). Т 4.4. Любое из чисел X, Y, Z положительно. Варианты ответа: а) (X > 0) Λ (Y > 0) V (Z > 0); б) (X > 0) V (Y > 0) Λ (Z > 0); в) (X > 0) V (Y > 0) V (Z > 0); г) (X > 0) Λ (Y > 0) Λ (Z > 0). Т 4.5. Любое из чисел X, Y, Z отрицательно. Варианты ответа: а) (X < 0) V (Y < 0) V (Z < 0); б) (X > 0) V (Y < 0) Λ (Z < 0); в) (X < 0) Λ (Y < 0) V (Z < 0); г) (X < 0) Λ (Y < 0) Λ (Z < 0). Т 4.6. Все числа X, Y, Z равны 12. Варианты ответа: а) (X = 12) V (Y = 12) Λ (Z = 12); б) (X = 12) Λ (Y = 12) V (Z = 12); в) (X = 12) Λ (Y = 12) Λ (Z = 12); г) (X = 12) V (Y = 12) V (Z = 12). Т 4.7. Только одно из чисел X, Y отрицательно. Варианты ответа: а) (X < 0) Λ (Y > 0) Λ (X > 0) Λ (Y < 0); б) (X < 0) V (Y > 0) V (X > 0) Λ (Y < 0); в) (X < 0) Λ (Y < 0) V (X > 0) Λ (Y < 0); г) (X < 0) Λ (Y > 0) V (X > 0) Λ (Y < 0). Т 4.8. Какое логическое выражение соответствует высказыванию: «Точка Х принадлежит интервалу (А, В)»? Варианты ответа: а) (X < A) или (X > B); б) (X > A) и (X < B); в) не (X < A) или (X > B); г) (X > A) или (X > B).
Таблицы истинности
Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных. Для составления таблицы необходимо: 1) выяснить количество строк в таблице (вычисляется как 2 n, где n – количество переменных); 2) выяснить количество столбцов = количество переменных + количество логических операций; 3) установить последовательность выполнения логических операций; 4) построить таблицу, указывая названия столбцов и возможные наборы значений исходных переменных; 5) заполнить таблицу истинности по столбцам. П 4.4. Построим таблицу истинности для выражения F = (A V B) Λ ( Количество строк = 22 (2 переменных) + 1(заголовки столбцов) = 5. Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (V, Λ, -, V, -) = 7. Расставим порядок выполнения операций: 1 5 2 4 3 (А V B) Λ ( Построим таблицу:
Логические схемы Из трех логических операций конъюнкции, дизъюнкции и инверсии (отрицания), выполняемых соответствующими элементами конъюнктром, дизъюнктром и инвертором, можно реализовать любые логические выражения.
Построение логических схем Правило построения логических схем: 1) Определить число логических переменных; 2) Определить количество логических операций и их порядок; 3) Изобразить для каждой логической операции соответствующий ей вентиль; 4) Соединить вентили в порядке выполнения логических операций. П 4.5. Пусть Х = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X 1) Две переменные – X и Y; 2) Две логические операции: 2 1 X 3) Строим схему:
Ответ: 1 V 0 Λ 1 = 1. П 4.6. Построить логическую схему, соответствующую логическому выражению F = X 1) Переменных две: Х и Y; 2) Логических операций три: конъюнкция и две дизъюнкции: 1 4 3 2 X 3) Схему строим слева направо в соответствии с порядком логических операций:
4) Вычислим значение выражения: F = 1 Тестовые задачи Т 4.9. Составьте таблицы истинности для следующих логических выражений: 1) F = (X 2) F = X 3) F = 4) F = Т 4.10. Для какого из указанных значений числа X истинно высказывание: (X > 4) \/ ((X > 1) U
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

 , (3)
, (3) . (4)
. (4) . (5)
. (5)

 и Z < 0.
и Z < 0.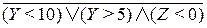 ; б)
; б)  ;
; ; г)
; г) 
 V
V  ).
). )
)


 Y
Y  X.
X.


 . Вычислить значения выражения для Х = 1, Y = 0.
. Вычислить значения выражения для Х = 1, Y = 0. ;
;
 = 0.
= 0. )
) 




