
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Таблицы истинности. Логические схемыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Таблицы истинности
Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных. Для составления таблицы необходимо: 1) выяснить количество строк в таблице (вычисляется как 2 n, где n – количество переменных); 2) выяснить количество столбцов = количество переменных + количество логических операций; 3) установить последовательность выполнения логических операций; 4) построить таблицу, указывая названия столбцов и возможные наборы значений исходных переменных; 5) заполнить таблицу истинности по столбцам. П 4.4. Построим таблицу истинности для выражения F = (A V B) Λ ( Количество строк = 22 (2 переменных) + 1(заголовки столбцов) = 5. Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (V, Λ, -, V, -) = 7. Расставим порядок выполнения операций: 1 5 2 4 3 (А V B) Λ ( Построим таблицу:
Логические схемы Из трех логических операций конъюнкции, дизъюнкции и инверсии (отрицания), выполняемых соответствующими элементами конъюнктром, дизъюнктром и инвертором, можно реализовать любые логические выражения.
Построение логических схем Правило построения логических схем: 1) Определить число логических переменных; 2) Определить количество логических операций и их порядок; 3) Изобразить для каждой логической операции соответствующий ей вентиль; 4) Соединить вентили в порядке выполнения логических операций. П 4.5. Пусть Х = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X 1) Две переменные – X и Y; 2) Две логические операции: 2 1 X 3) Строим схему:
Ответ: 1 V 0 Λ 1 = 1. П 4.6. Построить логическую схему, соответствующую логическому выражению F = X 1) Переменных две: Х и Y; 2) Логических операций три: конъюнкция и две дизъюнкции: 1 4 3 2
X 3) Схему строим слева направо в соответствии с порядком логических операций:
4) Вычислим значение выражения: F = 1 Тестовые задачи Т 4.9. Составьте таблицы истинности для следующих логических выражений: 1) F = (X 2) F = X 3) F = 4) F = Т 4.10. Для какого из указанных значений числа X истинно высказывание: (X > 4) \/ ((X > 1) → (X > 4))? а) 1; б) 2; в) 3; г) 4. Т 4.11. Постройте логическое выражение по логической схеме:
в) г)
Законы логики
Рассмотрим 6 законов логики и преобразование импликации: 1) коммутативность: A Ú B = B Ú A, A Ù B = B Ù A; 2) ассоциативность: A Ú (B Ú C) = (A Ú B) Ú C, A Ù (B Ù C) = (A Ù B) Ù C; 3) отрицание операнда: A Ù 4) дистрибутивность: A Ù (B Ú C) = (A Ù B) Ú (A Ù C), A Ú (B Ù C) = (A Ú B) Ù (A Ú C); 5) поглощения операнда A Ú (A Ù B) = A Ù (A Ú B) = А; 6) отрицание формулы (законы де Моргана):
5) преобразование импликации A ® B = Законы логики часто используют для упрощения логического выражения. П 4.7. Упростить логическое выражение 1) Избавимся от отрицания, используя закон 6 де Моргана
2) Применим закон поглощения операнда к формуле П 4.8. Упростить логическое выражение F = (A → B) 1) Избавимся от импликации (A → B) и (B → A), используя преобразование 7 (A → B) 2) Сгруппируем
Тестовые задачи Упростить выражения: Т 4.12. а) б) в) Преобразование высказываний в логическую формулу осуществляется следующим образом: - выделяют простые высказывания и обозначают их латинскими буквами; - записывают условия задачи на языке алгебры логики. П 4.9. Синоптик объявляет прогноз погоды на завтра и утверждает следующее: 1. Если не будет ветра, то будет пасмурная погода без дождя. 2. Если будет дождь, то будет пасмурно и без ветра. 3. Если будет пасмурная погода, то будет дождь и не будет ветра. Решение: 1. Выделим простые высказывания и запишем их через переменные: А – «Ветра нет». В – «Пасмурно». С – «Дождь». 2. Запишем логические функции (сложные высказывания).
а) «Если не будет ветра, то будет пасмурная погода без дождя» – б) «Если будет дождь, то будет пасмурно и без ветра» – в) «Если будет пасмурная погода, то будет дождь и не будет ветра» – Тестовые задачи Запишите в виде логической формулы следующие высказывания: Т 4.13. Если Иванов здоров и богат, то он здоров. Т 4.14. Число является простым, если оно делится только на единицу и само на себя. Т 4.15. Если число делится на 4, оно делится на 2. Т 4.16. Произвольно взятое число делится либо на 2, либо делится на 3. Т 4.17. Спортсмен подлежит дисквалификации, если он некорректно ведет себя по отношению к сопернику или судье, и если он принимал «допинг».
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.254 (0.01 с.) |

 V
V  ).
). )
)


 Y
Y  X.
X.


 . Вычислить значения выражения для Х = 1, Y = 0.
. Вычислить значения выражения для Х = 1, Y = 0. ;
;
 = 0.
= 0. )
) 

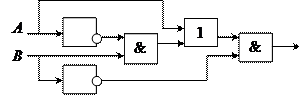
 а) б)
а) б)

 = F,
= F,  = A,
= A,  = T;
= T; .
. .
. ;
; , тогда
, тогда 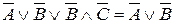 .
. ;
; и применим закон 3 отрицания операнда
и применим закон 3 отрицания операнда .
. . 4.13. а)
. 4.13. а)  ;
; . б)
. б)  ;
; в)
в) 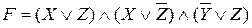 .
.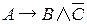 ;
; ;
; .
.


