Положительные и отрицательные

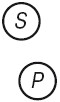
Виды

Простым называется суждение, не включающее других суждений. Они являются отражением одной-единственной связи объективного мира независимо от того, какая эта связь по содержанию. Напр., «Это – человек»; «У розы приятный запах» и др.

Простые суждения разнообразны по своим проявлениям. Они делятся на виды по логическим признакам: характер связки (качество и количество) субъекта и предиката, отношение между субъектом и предикатом.

По признаку отношения между субъектом и предикатом выделяются суждения:

а) атрибутивные (от лат. «свойство», «признак») – суждения о признаке предмета. В них отражается связь между предметом и его признаком, эта связь утверждается или отрицается. Атрибутивные суждения называются также категорическими, т. е. ясными, безусловными. Логическая схема атрибутивного суждения S-Р, где S – субъект суждения, Р – предикат, «-» – связка. Напр., «Адвокат встретился с обвиняемым». Категорические суждения делятся по качеству и количеству.

По качеству выделяют утвердительные и отрицательные суждения. Утвердительное выражает принадлежность предмету какого-либо свойства, отрицательное – отсутствие какого-либо свойства, они различаются качеством связки.

Суждение с отрицательным предикатом, но с утвердительной связкой рассматривается как утвердительное, напр., «Данное решение суда является необоснованным».

По количеству выделяют единичные, частные и общие суждения. Количественная характеристика выражается квантором общности. Единичным называется суждение, в котором что-либо утверждается или отрицается об одном предмете.

Напр., «Это здание – памятник архитектуры».

Частным называется суждение, в котором что-либо утверждается или отрицается о части предметов некоторого класса с помощью слов некоторые, многие, немногие, большинство, меньшинство, часть. Напр., «Часть преступлений относится к экономическим».

Общим называется суждение, в котором что-либо утверждается или отрицается обо всех предметах некоторого класса с помощью слов все, никто, любой, каждый. Напр.: «Все свидетели дали показания», «Никто не пришел на заседание». Иногда квантор не указывается, и тогда он определяется по смыслу, напр., «Равнодушие унижает»;

б) об отношениях между предметами (т. н. суждения с отношениями). Это могут быть отношения равенства, неравенства, пространственные, временные, причинно-следственные и др. Напр.: «А равно В», «Казань восточнее Москвы», «Семен отец Сергея» и др. Принята следующая символическая запись суждений с отношениями: хRу, где х и у – члены отношения, они обозначают понятия о предметах; В – отношение между ними. Запись читается: х находится в отношении R к у. Запись отрицательного суждения ⌉ (хВу) (неверно, что х находится в отношении В к у);

в) существования, выражающие сам факт существования или несуществования предмета суждения. Напр., «Существуют статистические законы». Предикатами этих суждений являются понятия о существовании или несуществовании предмета.

Классфикация

Объединяя количественную и качественную характеристики, атрибутивные суждения делятся на четыре группы: общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные.

Общеутвердительное – это суждение, общее по количеству и утвердительное по качеству. Напр., «Каждый, совершивший преступление, должен быть подвергнут справедливому наказанию». Схема такого суждения – «Все S суть Р», где кванторное слово «все» характеризует количество, утвердительная связка «суть» – качество суждения.

Общеотрицательное – суждение, общее по количеству и отрицательное по качеству. Напр., «Ни один невиновный не должен быть привлечен к уголовной ответственности». Схема такого суждения – «Ни одно S не есть Р». Кванторное слово «ни одно» характеризует количество, отрицательная связка «не есть» – качество суждения.

Частноутвердительное – суждение, частное по количеству и утвердительное по качеству. Напр., «Некоторые приговоры суда являются обвинительными». Схема такого суждения – «Некоторые S есть Р». Кванторное слово «некоторые» указывает на количество суждения, утвердительная связка, выраженная словом «есть», на его качество.

Частноотрицательное – суждение частное по количеству и отрицательное по качеству. Напр., «Некоторые приговоры суда не являются обвинительными». Схема такого суждения – «Некоторые S не есть Р». Кванторное слово «некоторые» указывает на количество суждения, отрицательная связка «не есть» – на его качество.

В логике принято сокращенное обозначение суждений по их объединенной классификации: А – общеутвердительные суждения; I – частноутвердительные; Е – общеотрицательные; О – частноотрицательные.

На языке логики предикатов рассмотренные суждения записывают следующим образом:

А – (Все S суть Р);

Е – (Ни одно S не есть Р);

I – (Некоторые S есть Р);

О – (Некоторые S не есть Р).

12. Распределенность терминов в суждении.*

В логических операциях с суждениями возникает необходимость установить, распределены или не распределены его термины – субъект и предикат. Термин считается распределенным, если он взят в полном объеме. Термин считается нераспределенным, если он взят в части объема.

Рассмотрим, как распределены термины в суждениях А, Е, I, О.

Суждение А (Все S суть Р). «Все студенты нашей группы (S) сдали экзамены (Р)». Субъект этого суждения («студенты нашей группы») распределен, он взят в полном объеме: речь идет обо всех студентах нашей группы. Предикат этого суждения не распределен, т. к. в нем мыслится только часть лиц, сдавших экзамены, совпадающая со студентами нашей группы.

 

Таким образом, в общеутвердительных суждениях S распределен, а Р не распределен. Однако в общеутвердительных суждениях, субъект и предикат которых имеют одинаковый объем, распределен не только субъект, но и предикат. К таким суждениям относятся обще-выделяющие суждения, а также определения, подчиняющиеся правилу соразмерности.

 

Суждение Е (Ни одно S не есть Р). «Ни один студент нашей группы (S) не является неуспевающим (Р)». И субъект, и предикат взяты в полном объеме. Объем одного термина полностью исключается из объема другого: ни один студент нашей группы не входит в число неуспевающих, и ни один неуспевающий не является студентом нашей группы. Следовательно, в общеотрицательных суждениях и S, и Р распределены.

 

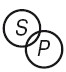
Суждение I (Некоторые S суть Р). «Некоторые студенты нашей группы (S) – отличники (Р)». Субъект суждения не распределен, т. к. в нем мыслится только часть студентов нашей группы, объем субъекта лишь частично включается в объем предиката: только некоторые студенты нашей группы относятся к числу отличников. Но и объем предиката лишь частично включается в объем субъекта: не все, а только некоторые отличники – студенты нашей группы. Следовательно, в частноутвердительном суждении ни S, ни Р не распределены.

 

Исключение из этого правила составляют частновыделяющие суждения, предикат которых полностью входит в объем субъекта. Напр., «Некоторые родители, и только они (S), являются многодетными (Р)». Здесь понятие «многодетные» полностью входит в объем понятия «родители». Субъект такого суждения не распределен, предикат распределен.

 

Суждение О (некоторые S не суть Р). «Некоторые студенты нашей группы (S) – не отличники (Р)». Субъект этого суждения не распределен (мыслится лишь часть студентов нашей группы), предикат распределен, в нем мыслятся все отличники, ни один из которых не включается в ту часть студентов нашей группы, которая мыслится в субъекте. Следовательно, в частноотрицательном суждении S не распределен, а Р распределен.

13. Отношения между суждениями по «логическому квадрату».

Общеутвердительное – это суждение, общее по количеству и утвердительное по качеству. «Все S суть Р»,

Общеотрицательное – суждение, общее по количеству и отрицательное по качеству. «Ни одно S не есть Р».

Частноутвердительное – суждение, частное по количеству и утвердительное по качеству. «Некоторые S есть Р».

Частноотрицательное – суждение частное по количеству и отрицательное по качеству. «Некоторые S не есть Р

В логике принято сокращенное обозначение суждений по их объединенной классификации: А – общеутвердительные суждения; I – частноутвердительные; Е – общеотрицательные; О – частноотрицательные.

А – (Все S суть Р);

Е – (Ни одно S не есть Р);

I – (Некоторые S есть Р);

О – (Некоторые S не есть Р).

Отношения между простыми суждениями обычно рассматриваются с помощью мнемонической схемы, называемой логическим квадратом. Его вершины символизируют простые категорические суждения – А, Е, I, О; стороны и диагонали – отношения между суждениями.

 

Среди сравнимых различают совместимые и несовместимые суждения.

Совместимыми являются суждения, которые одновременно могут быть истинными. Различают три вида совместимости: эквивалентность (полная совместимость), частичная совместимость (субконтрарность) и подчинение.

1. Эквивалентными являются такие суждения, которые имеют одинаковые логические характеристики: одинаковые субъекты и предикаты, однотипную – утвердительную или отрицательную – связку, одну и ту же выраженную квантором количественную характеристику.

С помощью логического квадрата отношения между простыми эквивалентными суждениями не иллюстрируются.

2. Частичная совместимость характерна для суждений I и О, которые могут быть одновременно истинными, но не могут быть одновременно ложными. При ложности одного из них другое будет истинным: ⌉ 1→0, ⌉ 0 → I. Напр., при ложности суждения «Некоторые злаки ядовиты» будет истинным суждение «Некоторые злаки не являются ядовитыми». В то же время при истинности одного из частных суждений другое может быть как истинным, так я ложным: I → (О ∨ ⌉0); O → (I ∨ ⌉I).

3. Подчинение имеет место между суждениями А и I, Е и О. Для них характерны следующие две зависимости.

При истинности общего суждения частное всегда будет истинным: А → I, Е → О. Напр., при истинности общего суждения «Всякое правоотношение регулируется нормами права» истинным будет и частное – «Некоторые правоотношения регулируются нормами права». При истинности суждения «Ни один кооператив не относится к государственным организациям» будет истинным и суждение «Некоторые кооперативы не относятся к государственным организациям».

При ложности частного суждения общее суждение также будет ложным: ⌉I → ⌉ A; ⌉ O → ⌉ E.

При подчинении остаются неопределенными следующие зависимости: при ложности общего суждения подчиненное частное может быть как истинным, так и ложным: ⌉ А → (I ∨⌉I ); ⌉ Е → (О ∨ ⌉О); при истинности подчиненного частного общее может быть как истинным, так и ложным: I → (А ∨ ⌉А); О → (Е ∨⌉Е).

14. Сложные суждения: общая характеристика и виды.*

Сложным называют суждение, состоящее из нескольких простых, связанных логическими связками. Различают следующие виды сложных суждений: 1) соединительные, 2) разделительные, 3) условные, 4) эквивалентные. Истинность таких сложных суждений определяется истинностью составляющих их простых.

Превращение

Преобразование суждения в суждение, противоположное по качеству с предикатом, противоречащим предикату исходного суждения, называется превращением. Превращение опирается на правило: двойное отрицание равносильно утверждению ⌉(⌉ р) ≡ р.

Превращать можно общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные суждения.

Преобразование суждения, в результате которого субъект исходного суждения становится предикатом, а предикат – субъектом заключения, называется обращением.

Обращение подчиняется правилу: термин, не распределенный в посылке, не может быть распределен в заключении.

Преобразование суждения, в результате которого субъектом становится понятие, противоречащее предикату, а предикатом – субъект исходного суждения, называется противопоставлением предикату.

Противопоставление предикату может рассматриваться как результат превращения и обращения: превращая исходное суждение S-Р, устанавливаем отношение S к не -Р; суждение, полученное путем превращения, обращается, в результате устанавливается отношение не -Р к S.

Заключение, полученное посредством противопоставления предикату, зависит от количества и качества исходного суждения.

 

24. Непосредственные умозаключения.

Непосредственные умозаключения - такие, в которых заключение выводится из одной посылки. Например, из суждения «Все адвокаты - юристы» можно получить новое суждение «Некоторые юристы - адвокаты». Непосредственные умозаключения дают нам возможность выявить знание о таких сторонах предметов, которое уже содержалось в исходном суждении, но не было явно выражено и явно осознано. В этих условиях мы делаем неявное - явным, неосознанное - осознанным.

К непосредственным умозаключениям относятся: превращение, обращение, противопоставление предикату, умозаключение по «логическому квадрату».

25. Умозаключение превращения. Превращение - такое умозаключение, в котором исходное суждение преобразуется в новое суждение, противоположное по качеству, и с предикатом, противоречащим предикату исходного суждения.

Чтобы превратить суждение, надо изменить его связку на противоположную, а предикат - на противоречащее понятие. Если посылка выражена не в явной форме, то надо преобразовать ее в соответствии со схемами суждений А, Е,I, О.

Все студенты первого курса изучают логику.

Ни один студент первого курса не изучает не логику.

Схема:

Все S суть Р.

Ни одно S не суть не-Р.

 

26. Умозаключение обращения.

Обращение - такое непосредственное умозаключение, в котором происходит перемена мест субъекта и предиката при сохранении качества суждения.

Обращение подчиняется правилу распределенности терминов: если термин не распределен в посылке, то он не должен быть не распределен и в заключении.

Если обращение ведет к изменению исходного суждения по количеству (из общего исходного получается новое частное суждение), то такое обращение называется обращением с ограничением; если обращение не ведет к изменению исходного суждения по количеству, то такое обращение является обращением без ограничения.

Примеры и схемы обращения:

А: Общеутвердительное суждение обращается в частноутвердительное.

Все адвокаты - юристы.

Некоторые юристы - адвокаты.

Все S суть Р.

Некоторые Р суть S.

27. Умозаключение противопоставления предикату.

Противопоставление предикату - это последовательное применение операций превращения и обращения - преобразование суждения в новое суждение, в котором субъектом становится понятие, противоречащее предикату, а предикатом - субъект исходного суждения; меняется качество суждения.

Например, из суждения «Все адвокаты - юристы» можно, противопоставляя предикат, получить «Ни один не-юрист не является адвокатом». Схематически:

Все S суть Р.

Ни одно не- Р не есть S.

28. Умозаключение по логическому квадрату. *

Умозаключение по «логическому квадрату». «Логический квадрат» - это схема, выражающая истинностные отношения между простыми суждениями, имеющими один и тот же субъект и предикат. В данном квадрате вершины символизируют известные нам по объединенной классификации простые категорические суждения: А, Е, О,I. Стороны и диагонали можно рассматривать как логические отношения между простыми суждениями (кроме эквивалентных). Так, верхняя сторона квадрата обозначает отношение между А и Е - отношение противоположности; нижняя сторона -отношение между О и I - отношение частичной совместимости. Левая сторона квадрата (отношение между А и I) и правая сторона квадрата (отношение между Е и О) - отношение подчинения. Диагонали обозначают отношения между А и О, Е и I, которые называются противоречием.

29. Простой категорический силлогизм: определение и структура.

Простой категорический силлогизм состоит из трех категорических суждений, два из которых являются посылками, а третье – заключением. Напр.,

«Обвиняемый имеет право на защиту.

Гусев – обвиняемый.

Гусев имеет право на защиту».

Расчленим суждения, из которых состоит силлогизм, на понятия. Этих понятий три, причем каждое из них входит в состав двух суждений: «Обвиняемый» – в 1-е (посылку) как субъект и во 2-е (посылку) как предикат; «имеет право на защиту» – в 1-е (посылку) и в 3-е (заключение) как их предикаты; «Гусев» – во 2-е (посылку) и в 3-е (заключение) как их субъекты.

Понятия, входящие в состав силлогизма, называют терминами силлогизма. Различают меньший, больший и средний термины.

Меньшим термином силлогизма называется понятие, которое в заключении является субъектом (в нашем примере понятие «Гусев»). Большим термином силлогизма называется понятие, которое в заключении является предикатом («имеет право на защиту»). Меньший и больший термины называются крайними и обозначаются соответственно латинскими буквами S (меньший термин) и Р (больший термин).

Каждый из крайних терминов входит не только в заключение, но и в одну из посылок. Посылка, в которую входит меньший термин, называется меньшей посылкой, посылка, в которую входит больший термин, называется большей посылкой.

В нашем примере большей посылкой будет первое суждение (1), меньшей – второе суждение (2).

Средним термином силлогизма называется понятие, входящее в обе посылки и отсутствующее в заключении (в нашем примере – «обвиняемый»). Средний термин обозначается латинской буквой М.

Обвиняемый (М) имеет право на защиту (Р).

Гусев (S) – обвиняемый (М).

Гусев (S) имеет право на защиту (Р).

Итак, простой категорический силлогизм – это умозаключение об отношении двух крайних терминов на основании их отношения к среднему термину.

Аксиома силлогизма обосновывает правомерность вывода, т. е. логического перехода от посылок к заключению: все, что утверждается или отрицается относительно всех предметов некоторого класса, утверждается или отрицается относительно каждого предмета и любой части предметов этого класса.

30. Фигуры и модусы категорического силлогизма.

В посылках простого категорического силлогизма средний термин может занимать место субъекта или предиката. В зависимости от этого различают четыре разновидности силлогизма, которые называют фигурами.

В первой фигуре средний термин занимает место субъекта в большей и место предиката в меньшей посылках.

Во второй фигуре – место предиката в обеих посылках.

В третьей фигуре – место субъекта в обеих посылках.

В четвертой фигуре – место предиката в большей и место субъекта в меньшей посылке.

Данные фигуры исчерпывают все возможные комбинации терминов.

Фигуры силлогизма – это его разновидности, различающиеся положением среднего термина в посылках.

Посылками силлогизма могут быть суждения, различные по качеству и количеству: общеутвердительные (А), общеотрицательные (Е), частноутвердительные (I) и частноотрицательные (О).

Разновидности силлогизма, различающиеся количественными и качественными характеристиками посылок, называются модусами простого категорического силлогизма.

Каждая фигура имеет свои особые правила, которые выводятся из общих.

Правила 1–й фигуры:

– большая посылка – общее суждение;

– меньшая посылка – утвердительное суждение.

1–я фигура – наиболее типичная форма дедуктивного умозаключения. Из общего положения, выражающего нередко закон науки, правовую норму делается вывод об отдельном факте, единичном случае, конкретном лице. Широко применяется данная фигура в судебной практике. Юридическая оценка (квалификация) правовых явлений, применение нормы права к отдельному случаю, назначение наказания за преступление, совершенное конкретным лицом, и другие судебные решения принимают логическую форму 1–ой фигуры силлогизма.

Правила 2–й фигуры:

– большая посылка – общее суждение;

– одна из посылок – отрицательное суждение.

Данная фигура применяется, когда необходимо показать, что отдельный случай (конкретное лицо, факт, явление) не может быть подведен под общее положение. Этот случай исключается из числа предметов, о которых сказано в большей посылке. В судебной практике 2–я фигура используется для заключений об отсутствии состава преступления в данном конкретном случае, для опровержения положений, противоречащих тому, о чем говорится в посылке, выражающей общее положение.

Правила третьей фигуры:

– меньшая посылка – утвердительное суждение;

– заключение – частное суждение.

Давая только частные суждения, 3–я фигура применяется чаще всего для установления частичной совместимости признаков, относящихся к одному предмету.

31. Общие правила силлогизма: правила терминов и

Правила посылок.

Из истинных посылок истинное заключение можно получить только в том случае, если соблюдаются правила силлогизма. Этих правил семь: три относятся к терминам и четыре – к посылкам.

1– е правило: в силлогизме должно быть только три термина. Вывод в силлогизме основан на отношении двух крайних терминов к среднему, поэтому в нем не может быть ни меньше, ни больше трех терминов. Нарушение этого правила связано с отождествлением разных понятий, которые принимаются за одно и рассматриваются как средний термин. Эта ошибка основана на нарушении требований закона тождества и называется учетверением терминов. Нельзя, напр., получить заключение из посылок: «Законы не создаются людьми» и «Закон – это нормативный акт, принятый высшим органом государственной власти», т. к. вместо трех терминов мы имеем дело с четырьмя: в первой посылке имеются в виду объективные законы, существующие независимо от сознания людей, во второй – юридический закон, устанавливаемый государством. Это два разных понятия, которые не могут связать крайние термины.

2– е правило: средний термин должен быть распределен хотя бы в одной из посылок. Если средний термин не распределен ни в одной из посылок, то связь между крайними терминами остается неопределенной. Напр., в посылках «Некоторые юристы (М) – члены коллегии адвокатов (Р)», «Все сотрудники нашего коллектива (S) – юристы (М)» средний термин (М) не распределен в большей посылке, т. к. является субъектом частного суждения, и не распределен в меньшей посылке как предикат утвердительного суждения. Следовательно, средний термин не распределен ни в одной из посылок. В этом случае необходимую связь между крайними терминами (S и Р) установить нельзя.

3-е правило: термин, не распределенный в посылке, не может быть распределен и в заключении. Напр.:

«Нравственные нормы (М) не санкционируются государством (Р).

ПРАВИЛА посылок

1– е правило: хотя бы одна из посылок должна быть утвердительным суждением. Из двух отрицательных посылок заключение с необходимостью не следует. Напр., из посылок «Студенты нашего института (М) не изучают биологию (Р)», «Сотрудники НИИ (S) не являются студентами нашего института (М)» нельзя получить необходимого заключения, т. к. оба крайних термина (S и Р) исключаются из среднего. Поэтому средний термин не может установить определенного отношения между крайними терминами.

2– е правило: если одна из посылок – отрицательное суждение, то и заключение должно быть отрицательным. Напр.:

Судья, являющийся родственником потерпевшего (М), не может участвовать в рассмотрении дела (Р).

Судья К. (S) – родственник потерпевшего (М).

Судья К. (S) не может участвовать в рассмотрении дела (Р).

3– е правило: хотя бы одна из посылок должна быть общим суждением. Из двух частных посылок заключение с необходимостью не следует. Если обе посылки – частноутвердительные суждения (II), то вывод сделать нельзя согласно 2-му правилу терминов: в частноутвердительном суждении ни субъект, ни предикат не распределены, поэтому и средний термин не распределен ни в одной из посылок. Если обе посылки – частно-отрицательные суждения (ОО), то вывод сделать нельзя согласно 1-му правилу посылок. Если одна посылка – частноутвердительная, а другая – частноотрицательная (IO или 0I), то в таком силлогизме распределенным будет только один термин – предикат частноотрицательного суждения. Если этим термином будет средний, то вывода сделать нельзя, т. к. согласно 2-му правилу посылок заключение должно быть отрицательным. Но в этом случае предикат заключения должен быть распределен, что противоречит 3-му правилу терминов: 1) больший термин, не распределенный в посылке, окажется распределенным в заключении; 2) если же больший термин распределен, то вывода не следует согласно 2-му правилу терминов.

4-е правило: если одна из посылок – частное суждение, то и заключение должно быть частным. Если одна посылка общеутвердительная, а другая – частноутвердительная (АI, IА), то в них распределен только один термин – субъект общеутвердительного суждения. Согласно 2-му правилу терминов, это должен быть средний термин. Но в таком случае два крайних термина, в т. ч. меньший, не будут распределены. Поэтому в соответствии с 3-м правилом терминов меньший термин не будет распределен в заключении, которое будет частным суждением. Если одна из посылок утвердительная, а другая – отрицательная, причем одна из них частная (ЕI АО, ОА), то распределенными окажутся два термина: субъект и предикат общеотрицательного суждения (ЕI) или субъект общего и предикат частного суждения (АО, ОА). Но в том и другом случае, согласно 2-му правилу посылок, заключение будет отрицательным, т. е. суждением с распределенным предикатом. А т. к. вторым распределенным термином должен быть средний (2-е правило терминов), то меньший термин в итоге окажется нераспределенным, т. е. заключение будет частным.

32. Особые правила каждой фигуры силлогизма. *

33. Сведение модусов II, III и IV фигур к модусам I фигуры.*

34. Условные, разделительные и условно-разделительные силлогизмы. *

35. Чисто условное умозаключение. *

36. Условно-категорическое умозаключение. *

37. Разделительно-категорическое умозаключение. *

38. Условно-разделительное умозаключение. *

39. Сокращенный силлогизм (энтимема). *

40. Сложные и сложносокращенные силлогизмы (полисиллогизм, эпихейрема, сорит).*

41. Индуктивные умозаключения.

Логический переход от знания об отдельных явлениях к знанию общему совершается в форме индуктивного умозаключения, или индукции (от лат. – наведение).

Индуктивным называется умозаключение, в котором на основании принадлежности признака отдельным предметам или частям некоторого класса делают вывод о его принадлежности классу в целом.

В истории физики, напр., опытным путем было установлено, что железные стержни хорошо проводят электричество. Такое же свойство было обнаружено у медных стержней и серебра. Учитывая принадлежность указанных проводников к металлам, было сделано индуктивное обобщение, что всем металлам свойственна электропроводность.

Посылками индуктивного умозаключения выступают суждения, в которых фиксируется полученная опытным путем информация о повторяемости признака Р у ряда явлений – S1, S2, Sn, принадлежащих одному и тому же классу К. Схема умозаключения имеет следующий вид: 1) S 1 имеет признак Р;

S 2 имеет признак Р;

................................

Sn имеет признак Р.

2) S1, S2….. Sn – элементы (части) класса К.

Всем предметам класса К присущ признак Р.

В основе логического перехода от посылок к заключению в индуктивном выводе лежит подтверждаемое тысячелетней практикой положение о закономерном развитии мира, всеобщем характере причинной связи, проявлении необходимых признаков явлений через их всеобщность и устойчивую повторяемость. Именно эти методологические положения оправдывают логическую состоятельность и эффективность индуктивных выводов.

Основная функция индуктивных выводов в процессе познания – генерализация, т. е. получение общих суждений. По своему содержанию и познавательному значению эти обобщения могут носить различный характер – от простейших обобщений повседневной практики до эмпирических обобщений в науке или универсальных суждений, выражающих всеобщие законы.

42. Полная и неполная индукция.

Полная индукция – это умозаключение, в котором на основе принадлежности каждому элементу или каждой части класса определенного признака делают вывод о его принадлежности классу в целом.

Индуктивные умозаключения такого типа применяются лишь в тех случаях, когда имеют дело с закрытыми классами, число элементов в которых является конечным и легко обозримым. Напр., число государств в Европе, количество промышленных предприятий в данном регионе, число субъектов федерации в данном государстве и т. п.

Неполная индукция – это умозаключение, в котором на основе принадлежности признака некоторым элементам или частям класса делают вывод о его принадлежности классу в целом.

1) S1 имеет признак Р;

S2 имеет признак Р;

................................

Sn имеет признак Р.

2) S1, S2….. Sn принадлежат классу К.

Классу К, по-видимому, присущ признак Р.

Неполнота индуктивного обобщения выражается в том, что исследуют не все, а лишь некоторые элементы или части класса – от S 1 до Sn. Логический переход в неполной индукции от некоторых ко всем элементам или частям класса не является произвольным. Он оправдывается эмпирическими основаниями – объективной зависимостью между всеобщим характером признаков и устойчивой их повторяемостью в опыте для определенного рода явлений. Отсюда широкое использование неполной индукции в практике. Так, напр., во время уборки урожая заключают о засоренности, влажности и других характеристиках большой партии зерна на основе отдельно взятых проб. В производственных условиях по выборочным образцам заключают о качестве той или иной массовой продукции.

Индуктивный переход от некоторых ко всем не может претендовать на логическую необходимость, поскольку повторяемость признака может оказаться результатом простого совпадения.

Тем самым для неполной индукции характерно ослабленное логическое следование – истинные посылки обеспечивают получение не достоверного, а лишь проблематичного заключения. При этом обнаружение хотя бы одного случая, противоречащего обобщению, делает индуктивный вывод несостоятельным.

43. Виды неполной индукции.

По способу отбора различают два вида неполной индукции: путем перечисления, получившую название популярной индукции, и путем отбора, которую называют научной индукцией.

Популярной индукцией (индукцией через простое перечисление) называют обобщение, в котором путем перечисления устанавливают принадлежность признака некоторым предметам или частям класса и на этой основе проблематично заключают о его принадлежности всему классу.

В процессе расследования преступлений часто используют эмпирические индуктивные обобщения, касающиеся поведения лиц, причастных к преступлению. Напр.: лица, совершившие преступления, стремятся скрыться от суда и следствия; угроза убийством часто приводится в исполнение. Такие опытные обобщения, или фактические презумпции, часто оказывают неоценимую помощь следствию, несмотря на то, что они являются проблематичными суждениями.

Популярная индукция определяет первые шаги и в развитии научных знаний. Любая наука начинает с эмпирического исследования – наблюдения над соответствующими объектами с целью их описания, классификации, выявления устойчивых связей, отношений и зависимостей. Первые обобщения в науке обязаны простейшим индуктивным заключениям путем простого перечисления повторяющихся признаков. Они выполняют важную эвристическую функцию первоначальных предположений, догадок и гипотетических объяснений, которые нуждаются в дальнейшей проверке и уточнении.

В условиях, когда исследуются лишь некоторые представители класса, не исключается возможность ошибочного обобщения.

Научной индукцией называют умозаключение, в котором обобщение строится путем отбора необходимых и исключения случайных обстоятельств.

В зависимости от способов исследования различают индукцию методом отбора (селекции) и исключения (элиминации).

Индукция методом отбора, или селективная индукция, – это умозаключение, в котором вывод о принадлежности признака классу (множеству) основывается на знании об образце (подмножестве), полученном методичным отбором явлений из различных частей этого класса.

Научной индукцией называют умозаключение, в котором обобщение строится путем отбора необходимых и исключения случайных обстоятельств.

В зависимости от способов исследования различают индукцию методом отбора (селекции) и исключения (элиминации).

Индукция методом исключения, или элиминативная индукция, – это система умозаключений, в которой выводы о причинах исследуемых явлений строятся путем обнаружения подтверждающих обстоятельств и исключения обстоятельств, неудовлетворяющих свойствам причинной связи.