Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Передача информации по каналу связи.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Любой канал связи или канал передачи можно рассматривать как некоторую систему, по которой передаётся информация – от входа к выходу.
При передаче информации по каналу связи на неё воздействуют помехи P. В общем случае количество входов и выходов может быть неограниченно большим. Пусть на вход поступает некоторый сигнал St. Система реализует на это воздействие появлением на выходе сигнала Sτ, который обязательно будет запаздывать по отношению к входному сигналу на некоторое время τ – время задержки в системе – и обязательно подвергнется некоторой модификации. Время задержки τ является, как правило, нежелательным свойством канала и должно быть по возможности минимизировано. С другой стороны, любое устройство хранения информации можно рассматривать как канал связи, также осуществляющий передачу информации со входа на выход, но одновременно обеспечивающий задержку этой информации на некоторое, желательно регулируемое и в принципе сколь угодно длительное время, которое можно назвать временем хранения информации. Модификация сигнала может носить характер искажений той или иной природы, но может представлять собой и полезный процесс, например, усиление, оптимальную фильтрацию и т.д. Существуют общие способы борьбы с помехами, пригодные для различных каналов связи. Прежде всего, желательно максимально снизить уровень помех и максимально повысить уровень полезного сигнала, увеличивая отношение сигнал/шум. Увеличение этого отношения может достигаться также за счёт соответствующего кодирования передаваемой информации, т.е. представления её в виде таких символов (например, импульсов определённой формы), которые чётко выделялись бы на фоне помех. Такое кодирование повышает помехоустойчивость передаваемой информации. Важной характеристикой канала является его пропускная способность. Чем больше информации будет передано по каналу связи в единицу времени, тем меньших энергетических затрат она потребует и тем меньше будет стоить передача единицы информации.
Множества сигналов.
При графическом представлении сигналы изображаются сложной совокупностью точек – кривой в простой области – в двумерном пространстве. В отличие от этого в теории сигналов вводят более сложные пространства – пространства сигналов, в которых каждый сигнал изображается простейшим элементом – точкой. Рассмотрим сигнал как элемент множества S. Само множество определяется некоторым свойством P, которое есть утверждение, справедливое для любого элемента множества. Условно это изображается так:
Гармонические сигналы. Обозначим через Sс множество всех гармонических сигналов (синусоидальных), т.е.
Утверждение Re Z, Im Z – действительная, мнимая, часть числа Z. Часто свойство P для конкретного множества можно указать в другой форме, например с помощью порождающего гармоническую функцию дифференциального уравнения
Периодические сигналы. Через Sп(T) обозначим множество периодических сигналов с периодом T.
Ограниченные сигналы. Множество сигналов, мгновенные значения которых ограничены по величине некоторым вещественным положительным числом A, обозначается:
Ясно, что Сигналы с ограниченной энергией. О сигналах из множества
Сигналы ограниченной длительности. Пусть
Заметим, что
Имея дело с множествами сигналов, полезно применять две элементарные операции теории множеств: объединение, определяемое как
Операторы ∪и ∩ могут быть применены для получения разбиения множества на ряд непересекающихся подмножеств. Мы говорим, что совокупность множеств {S1,S2,S3,...} образуют разбиением множества S, если S = S1 ∪ S2 ∪ S3 ∪...; Si ∩ Sj = ∅ для i≠j
При разбитии множества обычно получают более удобные подмножества. Разбиение можно произвести с помощью отношения эквивалентности, и часто это наиболее подходящий способ получения разбиения. Мы говорим, что два элемента эквивалентны, x~y, если отношение эквивалентности ~ определено для всех пар элементов и удовлетворяет следующим свойствам: x~x для любого x (рефлексивность), x ~ y ⇒ y ~ x ( симметрия ), x~y и y~z ⇒ x~z (транзитивность). Каждое отношение эквивалентности естественным образом порождает разбиение множества на ряд подмножеств Sx, называемых множествами эквивалентности, причём Sx включает все элементы, эквивалентные х:
С другой стороны, любое разбиение порождает отношение эквивалентности. Возьмём пример, известный из теории чисел. Рассмотрим разбиение множества всех целых чисел
Соответствующее отношение эквивалентности
Если мы исключим подмножество сигналов
(*) Это разбиение широко используется в двоичных системах передачи сигналов, причём одно значение двоичной величины соответствует всем сигналам из S+, а другое – всем сигналам из S –. Блок-схема двоичной системы передачи сигналов в этом случае имеет вид:
Хотя передаваемые сигналы могут быть только двух типов, в множество принимаемых сигналов входят сигналы, разнообразные по форме из-за шума и других помех, вносимых в канал передачи. Наблюдатель судит о том, какой сигнал из заданного разбиения (*) был передан по сигналу на выходе ограничителя. Не имеет значения, к какому из множеств S+ или S– отнести сигналы из подмножества S0, так как вероятность их появления при приёме ничтожна. Другой тип устройства для приёма двоичных сигналов, обладающий большей помехоустойчивостью, использует опорный сигнал ζ для разбиения принятых сигналов на два подмножества. Разбиение на подмножества S1 и S2, соответствующее принятию решения о том, какой из сигналов x1, или x2 был передан, выполняется на принятых сигналах y по условию:
Приёмное устройство в этом случае имеет вид:
Устройство содержит умножитель, интегратор, прерыватель и пороговое устройство. Опорный сигнал и величину порога выбирают по специальным алгоритмам оптимизации. Ещё одна возможность различия сигналов состоит в подсчёте числа пересечений нулевого уровня за определённый промежуток времени. Мы задаём разбиение
Можно также получить конечное разбиение
Схема реализует передачу и приём (N+1) – буквенного алфавита, соответствующего заданному (**) разбиению.
Накопление информации.
Способность к накоплению и хранению информации, т.е. наличие памяти, – одно из важнейших свойств любой кибернетической системы, без которого немыслимо её целесообразное функционирование. Физическую систему называют запоминающим устройством или, в информационном смысле, каналом накопления, если она обладает способностью обеспечивать достаточно длительный временной интервал между моментами прихода и использования информации. Это значит, что сигнал St, относящийся к моменту времени t, может быть воспроизведён с помощью такой системы в любое произвольное время τ в виде сигнала Sτ. Простейшая системная модель, обладающая свойством памяти, состоит из запоминающей среды. Основное свойство такой среды заключается в способности фиксировать и сохранять во времени следы информационных воздействий, а затем при определённых условиях полностью или частично воспроизводить их. Под влиянием входных сигналов Sвх(t1) и сигнала адреса Sа(t1) формируется некоторое адекватное функциям Sвх(t1) и Sа(t1) состояние среды:
Для этого необходимо иметь некоторую систему элементов, состояние которых можно было бы изменять желаемым образом при помощи сигнала S(t). Эти изменения могут происходить либо непрерывно, либо скачкообразно. В первом случае говорят о запоминающих элементах аналогового типа, во втором – об элементах дискретного типа. Необходимый элементный состав запоминающей среды определяет способ представления информации. В вычислительной технике широко используются элементы памяти дискретного типа пригодные для запоминания двоичного кода. Такой выбор обусловлен тем, что в физическом мире наиболее просто реализуются системы, обладающие двумя устойчивыми состояниями. Соответственно запоминающая среда должна содержать набор бистабильных элементов, которые могут находиться в двух устойчивых состояниях. Таким образом, среда – носитель информации – должна хранить в виде следа Ф(t) навязанное ей состояние, которое в идеальном накопителе должно оставаться неизменным в течение всего данного промежутка времени хранения. Однако под влиянием внешних воздействий, а также внутренних процессов, свойственных всякой системе, к началу считывания информации состояние среды неизбежно изменяется.
Воспроизведение информации.
Считывание (воспроизведение) информации – заключительный этап процессов памяти. При нарушении воспроизведения поведение системы меняется так, как если бы память в ней отсутствовала. Для воспроизведения информации из памяти необходимо активизировать определённую группу запоминающих элементов, составляющих ячейку памяти. При этом активирующее воздействие должно иметь такую природу, чтобы запоминающие элементы могли под его влиянием вырабатывать сигнал, соответствующий своему состоянию. Кроме того, оно должно быть индифферентным – одинаковым для любой ячейки независимо от содержания информации, хранящейся в ней. Если состояние запоминающих элементов однозначно соответствует сигналу, пришедшему на вход записи, то эта информация будет воспроизведена. При использовании некоторых физических сред считывание приводит к разрушению хранящейся в ячейки информации. В этом случае после каждого считывания необходимо производить запись той же самой информации в ту же ячейку. Запись информации в какую-либо ячейку и её считывание (с восстановлением) из какой-либо ячейки памяти производится за время, называемое периодом обращения. Время, необходимое для считывания информации из ячейки памяти, называют временем выборки. Одной из характеристик систем памяти является метод поиска информации. Поиск информации, по сути дела, сводится к поиску соответствующих запоминающих элементов (ячеек). Тип поиска, при котором, происходит обращение к какой-либо ячейке ЗУ по её номеру независимо от содержания искомой информации, называется адресным. Информация может быть выбрана и по некоторым её признакам или по некоторой известной её части. Такой принцип поиска – его называют ассоциативным – характерен, в частности, для биологических систем. При этом на входе появляется некоторый ключ – стимул, а на выходе памяти формируется специальная ответная реакция, связанная с ключом. Как стимул, так и ответная реакция представляют собой сложные сигналы – образы.
Помимо этого на входе может быть указана дополнительная информация, с помощью, которой можно более точно конкретизировать элемент, подлежащий выборке. С созданием ассоциативных ЗУ коренным образом меняется структура вычислительных машин и по-новому осуществляется управление сложными сигналами.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.60.175 (0.008 с.) |




 означает, что эти параметры могут произвольно выбираться из множества всех действительных чисел
означает, что эти параметры могут произвольно выбираться из множества всех действительных чисел  .
.

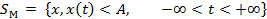


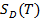 – это множество сигналов, которые равны нулю за пределами интервала времени – T ≤ t ≤ T:
– это множество сигналов, которые равны нулю за пределами интервала времени – T ≤ t ≤ T: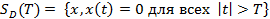



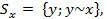
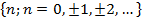


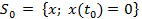 , то отношениеэквивалентности
, то отношениеэквивалентности