Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Маркшейдерские работы при проведенииСодержание книги
Поиск на нашем сайте Маркшейдерские работы при проведении буровзрывных работ……………………………………...64 Задачи для самостоятельных упражнений по разделу 4……..70 Список использованной литературы…………...72
Введение
Учебное пособие включает комплекс основных расчетно-графических работ, выполняемых маркшейдером при разработке месторождений полезных ископаемых открытым способом. По значению, трудоемкости и характеру данные работы относятся к капитальным и основным. Материал составлен в виде отдельных примеров по видам маркшейдерских работ и состоит из следующих тем: создание или реконструкция опорных и съемочных сетей на земной поверхности и в карьере, маркшейдерское обеспечение горно-капитальных и буровзрывных работ (составление плана-проекта), подсчет объемов горной массы при проходке горных выработок. В маркшейдерии изучение теоретических основ и их использование на практике при обучении специалистов возможно только при решении конкретных задач и примеров. Учебное пособие предусматривает выполнение заданий на лабораторных занятиях под руководством преподавателя и самостоятельную работу студента. При самостоятельной работе студентом выполняются задания на базе лабораторных работ, курса лекций и изучения технической литературы по вопросам, предусмотренных при изучении дисциплины «Маркшейдерия». Учебное пособие составлено в соответствии с рабочей программой обучения и учитывает изменения, произошедшие в изложении курса. Приводятся типовые примеры с последовательностью расчетов, выполняемых в период лабораторных занятий, и перечень дополнительных заданий и литература для самостоятельного изучения дисциплины и выполнения курсовой работы.
Создание И РЕКОНСТРУКЦИЯ Выбор знаков приращения координат
Положение точки (В) по отвесной (вертикальной) линии относительно точки (А) называется превышением Δ Z – разница высот между двух точек. В нашей стране высоты точек отсчитываются в Балтийской системе высот.
Δ Z = Z В – Z А, Z В = Z А ± Δ Z,
где - Z А, Z В – высотные отметки точек А и В.
Задача 5. Определить высоту точки В (Z В), если известна высота точки А (Z А) = 256,4 м и превышение между точками Δ Z = -7,7м. Решение. Z В = Z А - Δ Z – 256,4-7,7=248,7м.
Задача 6. Определить наклонную длину (L), угол наклона (δ) линии и ее уклон (i), если известны: Х А = 10 м., У А = 20 м, Z А=0 м, Х В = 100 м, У в=200 м, Z В = 50 м. Решение.
i = tgδ = Ответ.
По данным опорных маркшейдерских сетей и результатам топографической съемки для изображения земной поверхности и ее недр на горных предприятиях требуется большое количество чертежей (карт, планов). Для правильного их составления и чтения важно знать масштаб чертежей и его точность. Под масштабом понимается дробное число с числителем равным единице, а знаменателем – числу, показывающему степень уменьшения длины линии на чертеже к соответствующей длине этой же линии в натуре. Масштабы разделяются на численный, линейный и поперечный. Численный масштаб: 1/ М = d /L, где М - знаменатель масштаба; d – длина линии на чертеже; L – длина линии в натуре. Линейный масштаб – это прямая линия с нанесёнными на ней несколько равных (1 см.) отрезков. Линейный масштаб удобен при уменьшении или увеличении чертежей в процессе их копирования. Поперечный масштаб необходим при откладывании или измерении линий с большой точностью. Масштаб чертежей характеризуется точностью, т.е. расстоянием в натуре, соответствующим в данном масштабе отрезку 0,1 мм на чертеже. Точность масштаба: e М = 0,1 М, где М – знаменатель масштаба. Задача 7. Определить численный масштаб, если отрезок на чертеже d = 1 см, а соответствующая ему линия в натуре L = 10 м. Решение. 1/ М = d / L = 1 см/10 м = 10 см/1000 см = 1/1000. Задача 8. Определить точность масштаба при значении его знаменателя М =100. Решение. e М = 0,1 М = 0,1 ∙100 = 10мм = 0,01 м. Задачи для самостоятельных упражнений по разделу 1. 1. Выразить значение угла в виде десятичной дроби 2. Выразить значение угла 30,595830° + N ° в градусной мере. 3. Определить азимут географический Аг, если известен азимут магнитный А м = 110°+ N ° и магнитное склонение δ = +3°45². 4. Определить значение румба (r) линии, дирекционный угол (α) которой равен 345°+ 5. Определить высоту точки В (ZВ), если известна высота точки А (ZА) = 256,4 м + Nм и превышение между точками ΔZ = -7,7м + Nм. 6. Определить наклонную длину (L), угол наклона (δ) линии и ее уклон (i), если известны: Х А = 10 м + N м, У А = 20 м + Nм, Z А=0 м + N м, Х В = 100 м + N м, У В = 50 м + N м. 7. Определить численный масштаб, если отрезок на чертеже d = 1 см, а соответствующая ему линия в натуре L = 10м + N м. 8. Определить точность масштаба при значении его знаменателя М =100 N м. 9. Какие пункты являются исходными для построения опорных маркшейдерских сетей? 10. Какого класса точности должны быть пункты опорных маркшейдерских сетей? 11. Основные характеристики опорных маркшейдерских сетей и их плотность на территории горного предприятия.
Маркшейдерских сетей
Работа по созданию съемочных сетей на карьерах в соответствии с требованиями инструкции [1] выполняется по техническому проекту, в котором определяется схема, местоположение, количество пунктов съемочного обоснования, методика измерений и камеральная обработка. Плановое положение пунктов съемочных сетей (координаты X, Y) определяют: прохождением теодолитных ходов, геодезическими засечками, полярным способом. Высотные отметки (координата Z) - геометрическим и тригонометрическим нивелированием. Графическая основа съемочных сетей создается на планах земной поверхности и горных работ в масштабах 1:1000, 1:2000, 1:5000.
2.1. Определение плановых координат пунктов способом теодолитных ходов
Теодолитные хода прокладываются от пунктов опорных сетей в виде замкнутых или разомкнутых полигонов. Предельная угловая невязка теодолитного хода
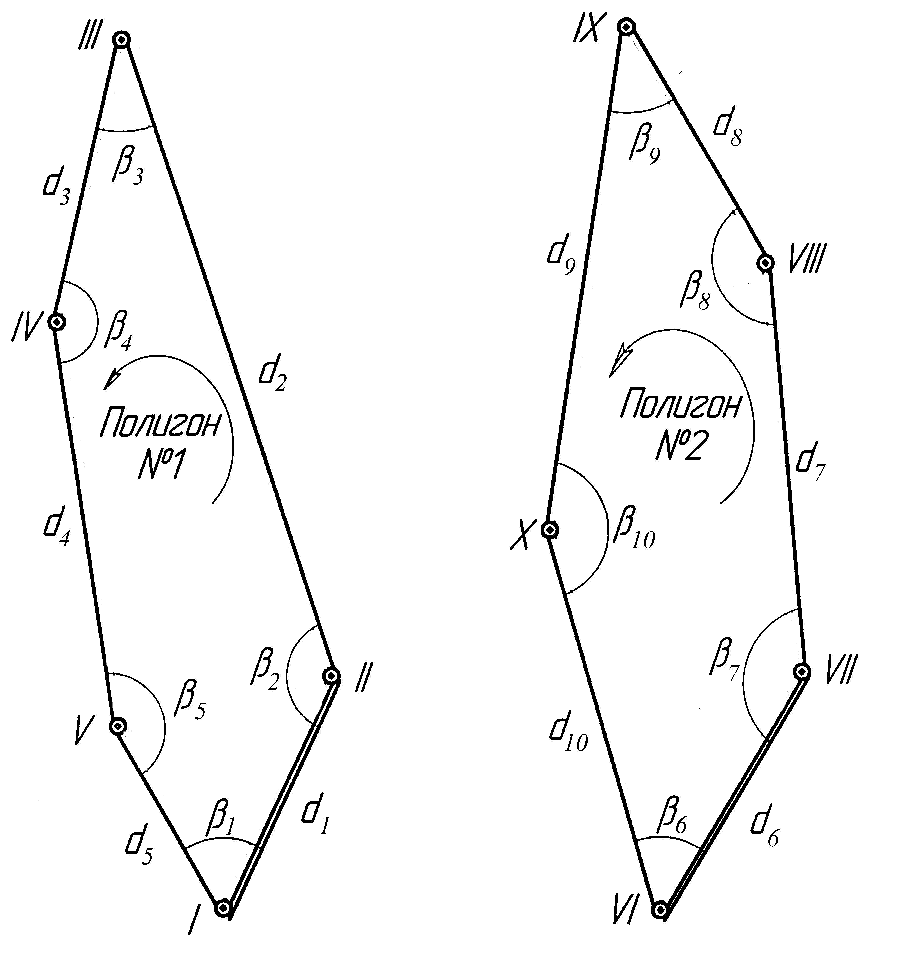
Решение задач. Задача 1. Пройти замкнутый теодолитный ход определить угловую и линейную невязки, уравнять ход, рассчитать координаты точек теодолитного хода. Решение. Исходные данные – дирекционные углы начальной стороны и координаты точки в опорной сети (рис.1): полигон № 1 aI-II = 75°55¢55; Х I = 640720,200; Y I = 6125312,050; полигон № 2 aVI-VII=70°30¢30²; Х VI = 640710,100; Y VI = 6125350,040.
Рис. 1. Замкнутый полигон теодолитного хода исходные стороны опорных сетей d – горизонтальные линии. Требуется измерить: полигон № 1: горизонтальные углы - b1, b2,... b5; горизонтальные линии - d 1, d 2,... d 5. полигон № 2: горизонтальные углы - b6, b7, … b10; горизонтальные линии - d 6, d 6, … d 10.
Методика измерений: - горизонтальные углы измеряются двумя приемами. Допустимое расхождение между приемами В расчеты принимаются среднеарифметические значения углов и длин. Требуется определить: координаты вершин точек теодолитного хода,
Методика вычислений: 1) рассчитывается угловая невязка хода
где n – число измеренных углов в полигоне; 2) при соблюдении условия 3) после распределения угловой невязки, решая прямую геодезическую задачу, рассчитывают дирекционные углы всех сторон полигона, приращения координат точек вершин хода и линейные невязки:
где 4) при соблюдении условия
5) после уравнивания (распределения линейной невязки) выполняется расчет координат пунктов полигона. Вычисление дирекционных углов и координат проводится по известным из курса геодезии формулам (решение прямой геодезической задачи). Пример расчета координат пунктов полигона представлен в табл. 2. 2.2. Определение плановых координат пунктов Таблица 2 Пример расчета координат точек теодолитного хода, полигон № 1
Продолжение таблицы 2 Пример расчета координат точек теодолитного хода, полигон № 2
Решение.
=
=
Контроль промежуточный: X I = =
Y I = =
Вычисление координат пункта Р1 из треугольника ll-lll-Р1
Измеренные углы: r 3=54°; r 4=80°; g 2=46° Исходные данные: ХII = 220 м; УII = 110 м; ХIII = 50 м; ХIII = 230 м; УIII = 290 м. (см. табл.2) Решение.
=
=
Контроль промежуточный:
Контроль решения прямой засечки: Из решения двух треугольников разница в координатах пункта Р 1 составляет которая не превышает 0,6 мм на плане в масштабе съемки (для масштаба 1:2000 Среднеарифметическое значение координат точки Р 1 из двух треугольников: Оценка точности планового положения пункта Р 1 характеризуется среднеквадратической погрешностью относительно пунктов опорной сети, величина которой не должна превышать 0,4 мм на плане в масштабе съемки [1] (для масштаба 1:2000 МР £ 0,8 м): для треугольника I-II- P 1
=
для треугольника II-III- P 1
= где B 1, В 2 - базис прямой засечки (расстояние между пунктами опорной сети), определяется решением обратной геодезической задачи: В 1 =
В 2=
В результате среднеквадратическая погрешность положения пункта Р 1 относительно пунктов опорной сети из двух треугольников составила 0,032 м и не превышает допустимой величины (0,8 м). Решение. Определяем дирекционные углы сторон:
a Р-II = aII-III + b1 = a Р-III = a I-III - b2 + 180º =
Определяем углы при точке Р:
g1 = 180º - b1 - b2 = 180° - 54° - 80°05´ = или g1 = aР-III - aР-II =
Определяем координаты точки Р:
Из решения двух треугольников разница в координатах точки Р 1 составляет
которая не превышает 0,6 мм на плане в масштабе съемки (для масштаба 1:2000 Среднеарифметическое значение координат точки Р 1 из двух треугольников:
Решение. Расчет среднеквадратической погрешности положения точки Р2: (исходные данные для расчета приведены в табл. 4). Вариант 1 (исходные пункты I, II, III)
Рис. 4 Варианты обратной засечки
Таблица 4
Исходные данные для расчета обратной геодезической засечки, взятые с плана участка карьера
Вариант 2 (исходные пункты II, III, IV)
Вариант 3 (исходные пункты I, II, IV)
Вариант 4 (исходные пункты I, III, IV)
По результатам оценки вариантов засечки получаем, что наиболее выгодная схема расположения пунктов в вариантах 3 и 4,
Вариант 3 Исходные данные (см. табл.4): X I =20 м; Y I =50 м; X II =220 м; Y II =110 м; X IV =200 м; Y IV =460 м; Измеренные углы: Углы Решение:
по разности дирекционных углов определяем:
Далее:
=
d = 239,789 м; d = 239,789 м; d ср = 239,789 м.;
=
= 254,522 м;
Вариант 4 Исходные данные:(см.табл.3): X I = 20 м; Y I = 50 м; X III = 230 м; Y III = 290 м; X IV = 200 м; Y IV = 460 м; Измеренные углы: Углы Решение:
по разности дирекционных углов определяем:
Далее:
d = 204,467 м; d = 204,467м; d ср= 204,467 м.;
= 254,521 м.
Контроль. По результатам расчета координат точки Р 2 из двух вариантов засечки имеем: Вариант 3 Вариант 4 Сравнивая два варианта решения, получаем разницу в координатах
что не превышает величины 0,4 мм на плане в масштабе съемки (0,8 м). Принимаем среднее значение координат точки Р2, полученных из двух вариантов засечки
Способ проф. Пащенкова В.З. Исходные данные (см. табл.3): X I =20 м; Y I =50 м; X II =220 м; Y II =110 м; X III = 230 м; Y III = 290 м; X IV =200 м; Y IV =460 м. Измеренные углы:
Решая обратную геодезическую задачу находим:
а =180,284 м; b =208,806 м.
Рис. 5. Схема решения обратной геодезической засечки
Решение: 1. 2.
3. 4. 5. 6. 7. 8. Для дополнительного контроля сравниваем полученные значения координат точки Р 2, с координатам
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

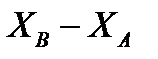


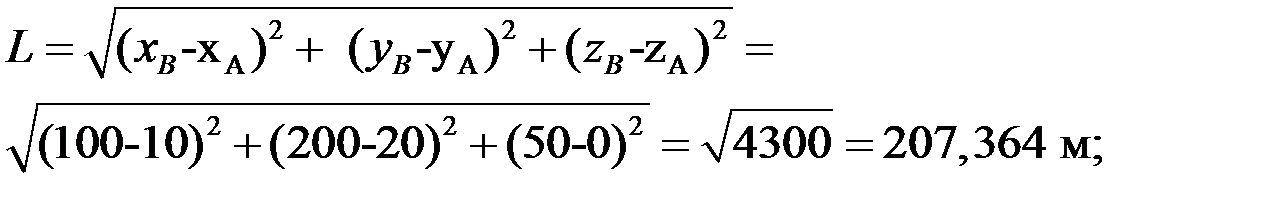
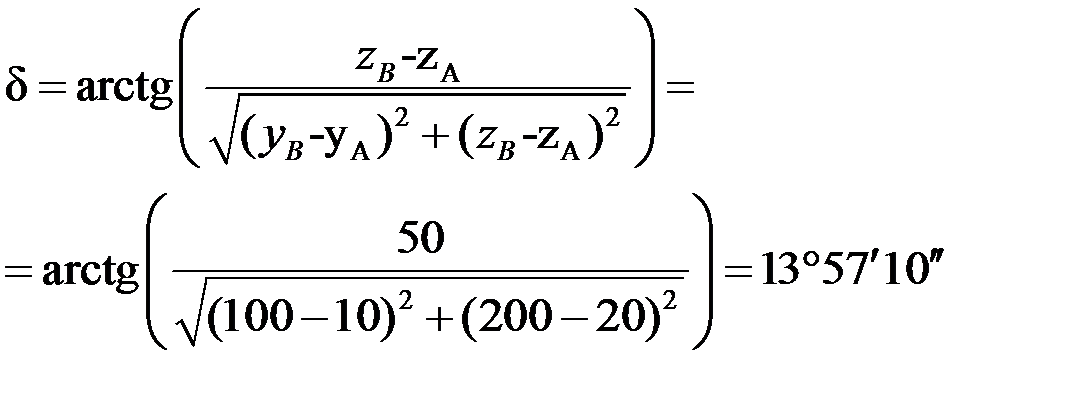 ;
; 0,001.
0,001.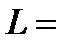 207,364 м., δ =
207,364 м., δ =  , i = 0,001.
, i = 0,001.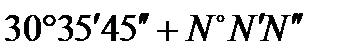 , где N –здесь и далее номер варианта.
, где N –здесь и далее номер варианта. .
. [1] или
[1] или  , где n – число измеренных углов в ходе, t – точность отсчитывания прибора (теодолита), но не ниже
, где n – число измеренных углов в ходе, t – точность отсчитывания прибора (теодолита), но не ниже 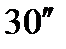 .
.

 , где t – точность отсчитывания прибора (теодолита) но не ниже 30сек.;
, где t – точность отсчитывания прибора (теодолита) но не ниже 30сек.;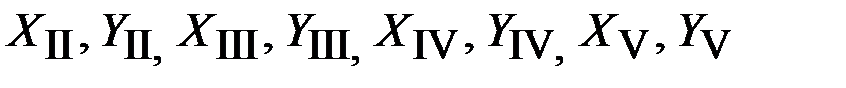 – полигон № 1;
– полигон № 1; – полигон № 2.
– полигон № 2.
 – внутренние углы;
– внутренние углы;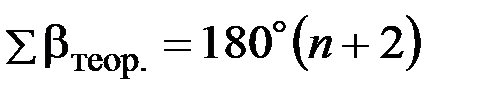 – внешние углы;
– внешние углы;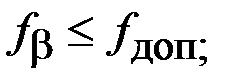
 ,
,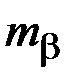 – среднеквадратическая погрешность измерения горизонтальных углов (20");
– среднеквадратическая погрешность измерения горизонтальных углов (20");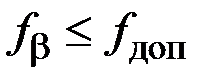 угловая невязка
угловая невязка  распределяется с обратным знаком во все углы полигона поровну;
распределяется с обратным знаком во все углы полигона поровну;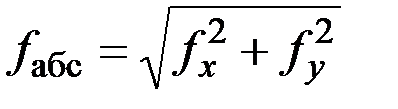 ;
; 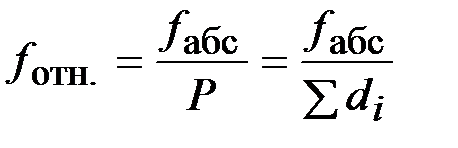 ;
; 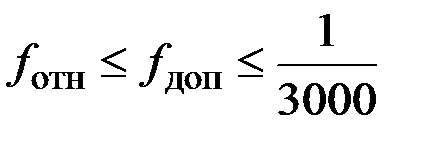 ,
,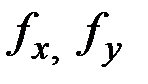 – линейные невязки хода; Р – периметр полигона;
– линейные невязки хода; Р – периметр полигона; 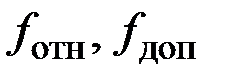 – относительная и допустимая невязки хода;
– относительная и допустимая невязки хода;  – горизонтальное проложение сторон полигона;
– горизонтальное проложение сторон полигона;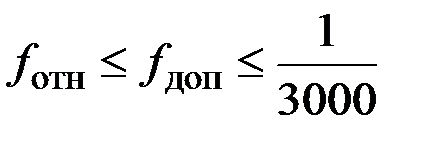 линейные невязки
линейные невязки 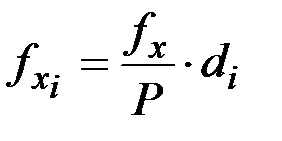 ;
; 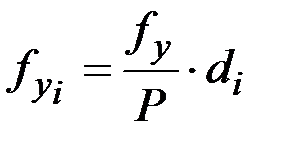 ;
;
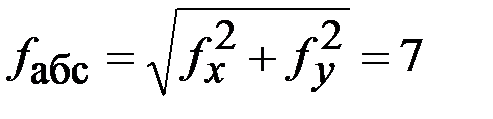 мм;
мм;  ;
; 
 IX
IX
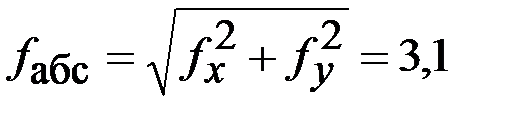 мм ;
мм ;  ;
;  =
=  =
= = 28,634 м,
= 28,634 м, =
=  =
= = 266,739 м.
= 266,739 м. =
= = 19,776 м.
= 19,776 м. =
= = 49,927 м.
= 49,927 м. =
=  =
= =28,711 м,
=28,711 м, =
=  =
= =266,178 м.
=266,178 м.



 =0,077 м,
=0,077 м,  =0,561 м,
=0,561 м, ,
,  £ 1,2 м).
£ 1,2 м). =28,672 м,
=28,672 м,  =266,458 м.
=266,458 м. =
= 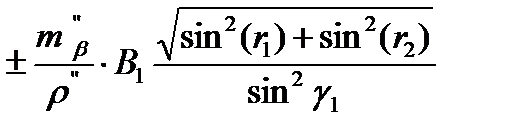 =
= = 0,030 м;
= 0,030 м; =
=  =
= = 0,032 м,
= 0,032 м, - среднеквадратическая погрешность измерения углов (15");
- среднеквадратическая погрешность измерения углов (15"); =
=  = 208,806 м;
= 208,806 м; =
=  = 180,277 м.
= 180,277 м. =
= 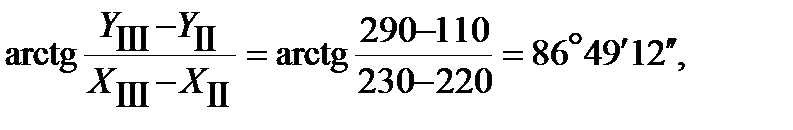
 + 54° =
+ 54° =  ;
; .
. ,
, -
- 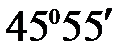 .
. ;
; =28,368 м,
=28,368 м,
 = 110 + (28,368 – 220) tg
= 110 + (28,368 – 220) tg  = 266,180.
= 266,180. =
=  = 0,049 м.
= 0,049 м.
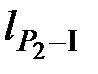 =204,8
=204,8
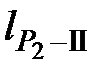 =239,7
=239,7
 =204,6
=204,6
 =239,7
=239,7
 =204,6
=204,6
 =267,3
=267,3
 =204,8
=204,8
 =239,7
=239,7
 =267,3
=267,3
 =204,8
=204,8
 =204,6
=204,6
 =267,3
=267,3
 =208,7
=208,7
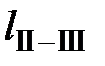 =180,3
=180,3
 =180,3
=180,3
 =172,6
=172,6
 =208,7
=208,7
 =350,5
=350,5
 =318,9
=318,9
 =172,6
=172,6
 =71
=71
 =77
=77
 =56
=56
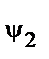 =50
=50
 =71
=71
 =50
=50
 =39
=39
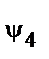 =50
=50

 =
=  = 0,032 м.
= 0,032 м. =
=  = 0,025 м.
= 0,025 м. =
=  = 0,025 м.
= 0,025 м. имеет наименьшее значение и не превышает величины 0,3 мм на плане в масштабе съемки (
имеет наименьшее значение и не превышает величины 0,3 мм на плане в масштабе съемки ( допустимая, составляет 0,6 м).
допустимая, составляет 0,6 м).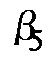 =55,360,
=55,360,  =87,240.
=87,240. £ 15''). Для исключения грубых ошибок при измерении углов на плане измеряются все углы в треугольнике и сумма их уравнивается к 1800.
£ 15''). Для исключения грубых ошибок при измерении углов на плане измеряются все углы в треугольнике и сумма их уравнивается к 1800.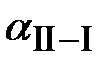 =
=  ;
;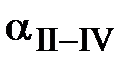 =
=  ;
; ;
; ;
;
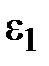
 =
=
 ;
; =
= 
 =
= 

 =
=
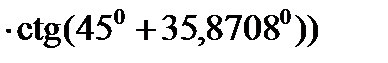
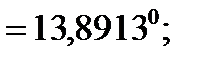
 =
=  +
+  =
= 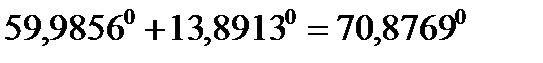 ;
; =
=  -
-  =
=  ;
;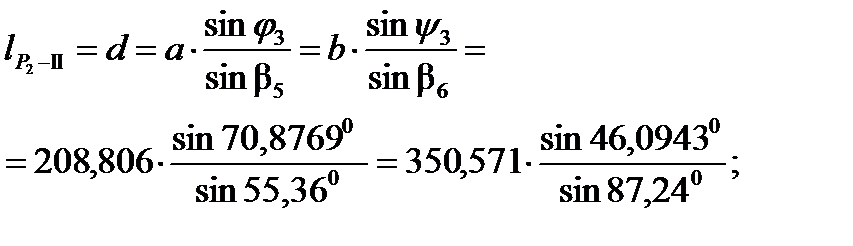

 =
=
 =322,93620 ;
=322,93620 ;
 =
=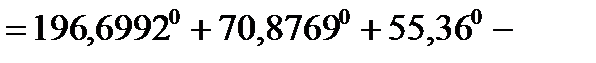
 =322,93620;
=322,93620;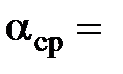 322,93620;
322,93620; =
=  =
= = 28,657 м;
= 28,657 м; =
=  =
=  =
= = 102,410,
= 102,410, 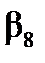 = 40,180.
= 40,180.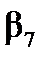 и
и  =
=  ;
; =
= 
 м;
м; м;
м; = 128,80610.
= 128,80610.


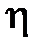 =
= 
 =
= 






 =
=  +
+ 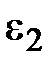 =
= 
 =
=  -
- 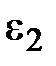 =
= 



 =
=
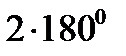 =369,99260;
=369,99260;
 =
=
 =369,99260;
=369,99260; 369,99260;
369,99260; +
+  =
=  = = 28,634 м,
= = 28,634 м, =
=  +
+  =
=  =
= = 28,657 м,
= 28,657 м,  = 254,522 м,
= 254,522 м, = 28,657 - 28,634 = 0,023 м;
= 28,657 - 28,634 = 0,023 м; = 254,522 - 254,521= 0,001 м,
= 254,522 - 254,521= 0,001 м, = 254,522 м.
= 254,522 м. ;
; .
.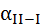 =
= 
 III-II =
III-II = 



 ;
;