Приведение закона Ампера к корректному физическому виду
Квантовый механизм электрического тока предполагает, что электрический ток является более сложным физическим явлением, чем сейчас описывается в электродинамике. Более того, в электродинамике до сих пор не известен физический смысл силы Ампера, поэтому в формуле, определяющей эту силу, есть величины, не имеющие физического смысла.
«Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные её элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила 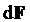 , с которой магнитное поле действует на элемент проводника , с которой магнитное поле действует на элемент проводника 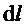 с током, находящегося в магнитном поле, равна с током, находящегося в магнитном поле, равна
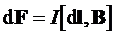 , (1) , (1)
где 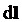 - вектор, по модулю равный - вектор, по модулю равный  и совпадающий по направлению с током, и совпадающий по направлению с током, 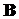 - вектор магнитной индукции. - вектор магнитной индукции.
Направление вектора 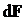 может быть найдено, согласно (1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в неё входил вектор может быть найдено, согласно (1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в неё входил вектор 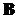 , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток». [3] , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток». [3]
Формула (1), определяющая силу Ампера физически не корректна: В векторном произведении 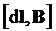 вектор вектор 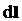 не имеет физической природы. не имеет физической природы.
Зная квантовый физический механизм электрического тока можно привести эту формулу к виду, в котором все величины будут иметь физический смысл. Для этого нужно заменить не физическую величину 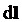 в векторном произведении формулы (1) на физическую векторную величину в векторном произведении формулы (1) на физическую векторную величину 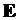 . Выведем её из закона Ома. . Выведем её из закона Ома.
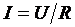 , (2) , (2)
Учитывая, что 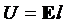 , ,
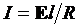 , (3) , (3)
Заменяя 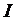 в формуле (1), получим: в формуле (1), получим:
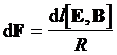 , (4) , (4)
где 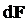 - сила Ампера, - сила Ампера,
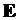 - вектор напряженности электрического поля. Этот вектор направлен вдоль проводника и является величиной, имеющей физический смысл. - вектор напряженности электрического поля. Этот вектор направлен вдоль проводника и является величиной, имеющей физический смысл.
 - вектор магнитной индукции внешнего магнитного поля, в которое помещен проводник с током. Это также величина, имеющая физический смысл. - вектор магнитной индукции внешнего магнитного поля, в которое помещен проводник с током. Это также величина, имеющая физический смысл.
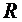 - электрическое сопротивление проводника. - электрическое сопротивление проводника.
Формула (4) выражает закон Ампера для участка цепи – потребителя тока, приведенный к корректному физическому виду в рамках классической электродинамики. Левая часть выражает изменение гравитационного поля проводника, правая – изменение электромагнитного поля. Формулу (4) можно также преобразовать для участка цепи – источника тока и полной цепи электрического тока.
Закон Ампера для участка цепи – источника тока выглядит следующим образом:
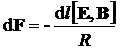 , (5) , (5)
И для полной цепи электрического тока:
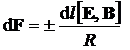 . (6) . (6)
Знак (-) перед правой частью уравнения (5) означает изменение потока энергии при переходе проводника на участок цепи – источник тока.
Таким образом, даже в рамках классической электродинамики можно вывести формулы для определения силы Ампера для цепи – потребителя тока, цепи – источника тока и полной цепи. Однако вывод этой формулы не даёт механизма электрического тока.
Для того, чтобы понять физическую природу возникновения силы Ампера, рассмотрим этот физический феномен с позиций квантовой теории электрического тока.
|