Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение остовных деревьевСодержание книги
Поиск на нашем сайте
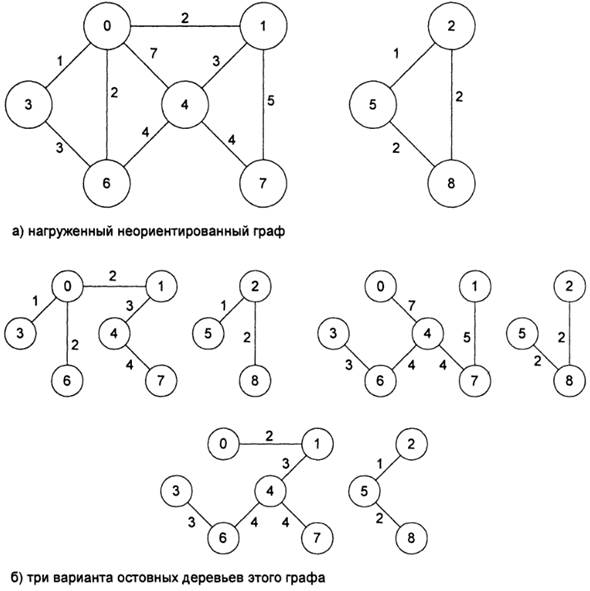
Остовиым деревом (скелетом) неориентированного графа называется его подграф, не имеющий циклов и содержащий все вершины исходного графа. Так, например, для нагруженного графа, изображенного на рис. 9, а, скелетами являются все его подграфы, изображенные на рис. 9, б.
Рис. 9. Нагруженный неориентированный граф и его остовные поддеревья
Строго говоря, то, что изображено на рис. 9, б, не является деревом, поэтому следовало бы говорить не об остовном дереве, а, скорее, об остовном лесе. Тем не менее в дальнейшем мы не будем уточнять, идет ли речь об одном или нескольких деревьях, представляющих остов графа. Варианты скелетов исходного графа, изображенные на рис. 9, б, имеют различный суммарный вес ребер графа. В первом варианте сумма весов ребер скелета равна 15, во втором варианте— 27, и в третьем варианте— 19. В разных ситуациях бывает необходимо найти остовное дерево с максимальным или минимальным общим весом ребер. Так первое поддерево имеет минимальный суммарный вес из всех возможных поддеревьев. Второе поддерево— максимальный. Поставим задачу найти минимальное остовное дерево (т. е. остовное дерево минимального суммарного веса ребер) для заданного неориентированного графа. Разумеется, поиск максимального остовного дерева будет производиться по точно такому же алгоритму. Первый из предлагаемых алгоритмов принадлежит классу так называемых жадных алгоритмов. Этот алгоритм пытается найти решение поставленной задачи в лоб, стараясь найти минимальное остовное дерево последовательным отбором ребер с минимальным весом, следя за тем, чтобы получающийся граф не имел циклов. Разумеется, для этого необходимо сначала отсортировать все ребра графа по возрастанию их весов. Лучше всего, если граф с самого начала представлен списком ребер, в этом случае сортировка будет наиболее естественной. Но даже и в других случаях сортировка ребер графа по весу занимает не слишком много времени— в худшем случае M x log2M, где М — количество ребер графа. Подходящим способом сортировки ребер будет организация списка ребер в виде пирамиды — в этом случае сортировку можно совместить во времени с основной работой алгоритма. После того как ребра будут выстроены в упорядоченный список или в пирамиду, жадный алгоритм выбирает ребра по очереди, начиная с ребер с наименьшим весом, и пытается включить каждое очередное ребро в строящееся дерево. Очередное ребро не удается включить в дерево, если оно замыкает какой-либо цикл в графе. Проверить этот факт можно, если удастся выяснить, принадлежат ли оба конца очередного ребра уже построенной части остовного дерева. Отсюда следует следующий алгоритм, называемый также алгоритмом Крускала (J. В. Kruskal).
Алгоритм Крускала
После сортировки ребер по весу строящееся остовное дерево организуется в виде отдельных фрагментов этого дерева, в которые в каждый момент времени включены все вершины графа. В начале работы каждая вершина графа представляет собой отдельную компоненту, а соединяющих их ребер пока вообще нет. Каждое вновь включаемое ребро соединяет две отдельные компоненты в одну, таким образом, полное остовное дерево будет построено после N-1включения ребра. Разумеется, очередное ребро можно включить в дерево, только если его концы принадлежат разным компонентам, в противном случае в компоненте образуется цикл. Таким образом, если очередное ребро соединяет вершины, принадлежащие одной связной компоненте, то такое ребро не включается в строящееся остовное дерево и игнорируется
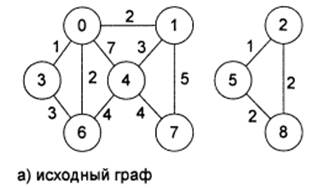
Рис. 10. Алгоритм Крускала построения минимального остовного дерева графа
Для хранения информации о компонентах строящегося дерева предлагается структура данных в виде массива, каждый i-й элемент которого содержит ссылку на одну из вершин компоненты, содержащей i-ю вершину. Фактически такой массив является одним из способов представления дерева компонент (точнее, леса из нескольких деревьев), в котором ссылки из узлов дерева проводятся от потомков к предкам. На рис. 10.б представлена последовательность этапов при построении компонент остовного дерева согласно жадному алгоритму. В качестве исходного графа выбран граф рис. 10.а. Первоначально остовное дерево состоит из отдельных вершин исходного графа, жадный алгоритм постепенно добавляет к нему ребра, начиная с ребер с наименьшим весом. На рис. 10.бпоказаны 8 последовательных этапов построения остовного дерева согласно жадному алгоритму. На каждом этапе в остовное дерево включается новое ребро. Ребра, замыкающие цикл в уже построенной части, игнорируются алгоритмом. В листинге показана реализация алгоритма Крускала построения минимального остовного дерева. Метод minSkeieton графа получает в качестве аргумента выходной поток для печати в него информации о ребрах графа, включаемых в остовное дерево. Второй аргумент— это объект, задающий нагрузку на ребра графа. Информация о структуре минимального остовного дерева выводится в выходной поток в виде последовательности пар целых чисел — номеров вершин, задающих ребра графа, а общий полученный вес этого остовного дерева выдается в качестве результата работы функции. На первом этапе работы алгоритма строится пирамида из ребер графа. В каждый узел пирамиды заносится информация о номерах соединяемых этим ребром вершин и о весе ребра. Информация о ребрах графа берется из матрицы смежности графа и объекта класса GraphWeight, задающего нагрузку на ребра. На втором этапе начинается построение остовного дерева, информация о котором хранится в массиве. Каждый раз, как только очередное ребро попадает в остовное дерево, информация о нем выводится в выходной поток. Листинг: Реализация алгоритма Крускала построения минимального остовного дерева Файл listgraph. h // Класс ListGraph задает структуру L-графа class ListGraph { // Массив списков дуг List<int> *graph; // Количество вершин графа int vertexNumber; public: // Конструктор создает массив пустых списков ListGraph(int n): vertexNumber(n), graph(new List<int>[n]) {} // Деструктор уничтожает списки дуг ~ListGraph() { delete [] graph; } // Функция подсчета числа вершин просто выдает // ранее сохраненное значение int vertexCount() const {return vertexNumber; } // Основные методы работы с графом void addArc(int from, int to); bool hasArc(int from, int to) const; // Алгоритм Крускала нахождения минимального остовного дерева double minSkeleton(std:rostream & out, const GraphWeight & gw); };
Файл Arc. h // Структура ребра для алгоритма Крускала: сравнение ребер // происходит по их весам
struct Arc { int from, to; double weight; Arc(int from = 0, int to = 0, double weight = 0) : from(from), to(to), weight(weight) {} Arc(const Arc & arc) : from(arc.from), to (arc.to), weight(arc.weight) {} Arc & operator = {const Arc & arc) { from - arc.from; to - arc.to; weight = arc.weight; } bool operator < (const Arc & arc) { return weight < arc.weight; } bool operator <= (const Arc & arc) { return weight <= arc.weight; } bool operator > (const Arc & arc) { return weight > arc.weight; } bool operator >= (const Arc & arc) { return weight >= arc.weight; } bool operator == (const Arc & arc) { return weight == arc.weight; } bool operator!= (const Arc & arc) { return weight!= arc.weight; } std::ostream & operator «(std::ostream & out, const Arc & arc);
Файл listgraph. cpp // Собственно алгоритм Крускала double ListGraph::minSkeleton( // Выходной поток для вывода результирующей информации: std::ostream & out, // Нагрузка на ребра графа: const GraphWeight & gw) { // Суммарный вес найденного минимального остовного дерева: double weight = 0; // Пирамида, содержащая информацию о ребрах графа: ArrayHeap<Arc> arcs(vertexNumber * vertexNumber / 2); // Структура узла в лесе, представляющем частично построенное // минимальное остовное дерево struct SkeletonNode { int node; // номер узла исходного графа int next; // ссылка на родительский узел // Конструкторы: SkeletonNode(int n = 0): node(n), next(-l) {} SkeletonNode(const SkeletonNode & node): node(node.node), next(node.next) {} }; // Начальное заполнение пирамиды ребер: // просматриваются все ребра графа, //и информация о них заносится в пирамиду, for (int i = 0; i < vertexNumber; i++) { Iterator<int> *neighbors = graph[i].iterator(); while (neighbors->hasMoreElements()) { int j = **neighbors; } // Граф неориентированный, поэтому для исключения дублирования // информации рассматриваются только дуги, ведущие из вершины // с меньшим номером в вершину с большим номером. Петли // (если они есть) сразу же исключаются, if (i < j) { // Добавление ребра в пирамиду: arcs += Arc(i, j, gw.arcLength(i, j)); } ++*neighbors; } delete neighbors; // Начальное заполнение леса: каждая вершина графа представляет // собой отдельное дерево, состоящее из единственной вершины. SkeletonNode skeleton[vertexNumber]; for (int i = 0; i < vertexNumber; i++) { skeleton[i] = SkeletonNode(i); } // Основной цикл по ребрам, включенным в пирамиду while (!arcs.empty()) { // Очередное ребро берется с вершины пирамида и исключается из нее Arc nextArc = *arcs; arcs, remove (); // u и v - концы выбранного ребра int u = nextArc. from, v = nextArc.to; // Следующие два цикла находят корни деревьев, // содержащих эти вершины: while(skeleton[u].next! = -1) u = skeleton[u].next; while(skeleton[v].next!= -1) v = skeleton[v].next; if (u!= v) { // Ребро включается в остовное дерево,... out «nextArc «"; "; weight += nextArc.weight; //... а два дерева соединяются в одно. skeleton[u]-next = v; }return weight;}
При попытке вычислить минимальное остовное дерево для графа, приведенное на рис. 10 а, с помощью вызова метода: cout «testGraph.minSkeleton(cout, arcsWeight); В стандартный выходной поток будет выведена следующая информация: (2,5); (0,3); (5,8); (0,6); (0,1); (1,4); (4,7); 15 Что и свидетельствует о том, что минимальное остовное дерево построено правильно, поскольку содержит ребра (2, 5), (0, 3), (5, 8), (0, б), (0, 1), (1, 4), (4, 7) и суммарный вес всех ребер составляет минимально возможную величину 15. Еще один алгоритм построения минимального остовного дерева напоминает алгоритм Дейкстры для поиска наименьшего пути между двумя вершинами в графе и носит название алгоритма Прима (R. С. Prim). Алгоритм Прима
В этом алгоритме построение остовного дерева начинается с одной вершины, к которой затем добавляются ребра таким образом, чтобы каждое новое ребро одним своим концом опиралось в уже построенную часть дерева, а другой конец лежал бы в множестве еще не присоединенных к дереву вершин. Из всех таких ребер на каждом шаге выбирается ребро с наименьшим весом. Для того чтобы выбор ребра был бы наиболее эффективен, так же, как и в алгоритме Дейкстры, в алгоритме Прима используется промежуточная структура данных — массив, элементы которого содержат информацию о расстоянии от каждой из вершин до уже построенной части остовного дерева. Таким образом, с помощью однократного просмотра такого массива всегда можно выбрать ребро минимальной длины. Будем считать, что вершины, не соединенные ребрами с уже построенной частью остовного дерева, находятся от этой части на бесконечно большом расстоянии. После того как очередная вершина будет выбрана и присоединена к остовному дереву, все инцидентные ей ребра просматриваются, чтобы скорректировать информацию о расстояниях. Эта часть алгоритма также очень похожа на соответствующую коррекцию массива расстоянии из алгоритма Дейкстры. Если оказывается, что очередная выбранная вершина находится на бесконечно большом расстоянии от уже построенной части дерева, то это означает, что завершено построение дерева для одной компоненты связности графа и, значит, одного остовного дерева для графа построить невозможно (в этом последнем случае стоит говорить об остовном лесе). Если для графа, изображенного на рис. 10 а, начать поиск минимального остовного дерева с вершины 0, то к дереву будут последовательно присоединяться ребра 0—3 (длиной 1), 0—1 (2), 0—6 (2), 1—4 (3), 4— 7 (4), вершина 2 (+∞), 2—5(1), 2—8 (2). На рис. 11 показана последовательность построения минимального остовного дерева для графа, изображенного на рис. 10 а. Реализация алгоритма Прима показана в листинге в виде определения метода minSkeletonPrim, который так же, как и метод minSkeleton, в качестве аргумента получает выходной поток для печати информации о найденных ребрах минимального остовного дерева, а в качестве результата выдает суммарный вес полученного остовного дерева.
Листинг: Алгоритм Прима нахождения минимального остовного дерева
double ListGraph::minSkeletonPrim( // Выходной поток для вывода результирующей информации: std::ostream & out, // Нагрузка на ребра графа: const GraphWeight & gw) { // Множество непройденных вершин (сначала - все вершины) Set notPassed(0, vertexNumber-1); notPassed.addScale(0, vertexNumber-1); // Массив расстояний от вершин до уже построенной части double *dist - new double[vertexNumber]; // Массив направлений от новых вершин к уже построенной части double *ends = new double[vertexNumber]; // Инициализация массивов расстояний и направлений for (int i = 0; i < vertexNumber; i++) { dist[i] = INFINITY; ends[i] = -1; } // Суммарный вес построенной части дерева double sumWeight =0; // Основной цикл поиска новых вершин while (!notPassed.empty()) { // Поиск ближайшей вершины double minDist = INFINITY; Iterator<int> *iVertices = notPassed.iterator(); int minVertex = **iVertices; while (iVertices->hasMoreElements()) { int nextVertex = **iVertices; if (dist[nextVertex] < minDist) { minDist = dist[nextVertex]; minVertex = nextVertex; } ++*iVertices; } delete iVertices; if (dist[minVertex] < INFINITY) { // Присоединяем очередное ребро out << "(" << ends[minVertex] << "," << minVertex <<”);”; sumWeight += minDist; } notPassed -= minVertex; // Новая вершина присоединена; // корректируем информацию о расстояниях Iterator<int> *neighbors = graph[minVertex].iterator(); while (neighbors->hasMoreElements()) { int next = **neighbors; if (notPassed.has(next)&& gw.arcLength(minVertex, next) < dist[next]) { dist[next] = gw.arcLength(minVertex, next); ends[next] = minVertex; } ++*neighbors; } delete neighbors; } return sumWeight; }
Рис. 11. Этапы построения остовного дерева согласно алгоритму Прима Если применить метод minSkeietonPrim к графу, изображенному на рис. 10 а cout «testGraph.minSkeleton(cout, arcsWeight); то, разумеется, результат будет примерно тем же самым, что и при применении метода minskeieton, реализующего жадный алгоритм: (0,3); (0,1); (0,6); (1,4); (4,7); (2,5); (2,8); 15 Алгоритмы имеют разную производительность на различных графах. Скорость работы алгоритма Крускала зависит, прежде всего, от количества ребер в графе и слабо зависит от количества вершин. Напротив, скорость работы алгоритма Прима определяется количеством вершин и слабо зависит от числа ребер. Следовательно, алгоритм Крускала следует применять в случае неплотных или разреженных графов, у которых количество ребер мало по сравнению с количеством ребер у полного графа. Если известно, что ребер в графе достаточно много, то для поиска минимального остовного дерева лучше применять алгоритм Прима.
Контрольные вопросы
Задания для практической работы
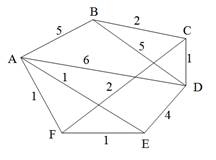
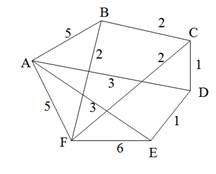
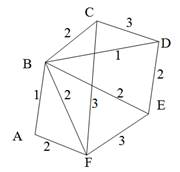
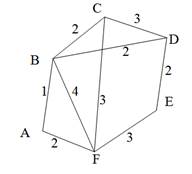
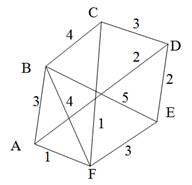
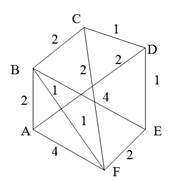
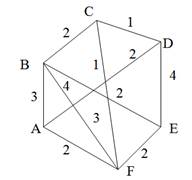
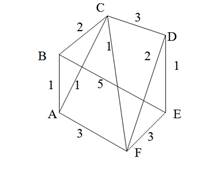
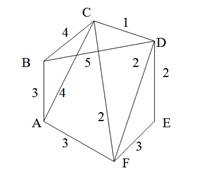
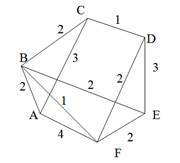
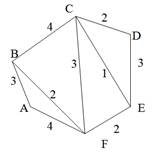
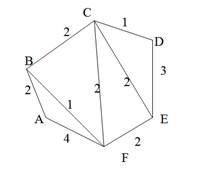
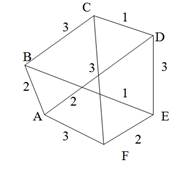
Выберите граф и выполните следующие операции: a) представить граф в виде массива; b) представить граф в виде матрицы смежности; c) представить граф в виде связанного списка; d) представить граф в виде списка дуг; e) предусмотреть возможность преобразования структур графа; f) реализовать обход графа в глубину и ширину; g) определить если имеются путь и контур Эйлера; h) реализовать поиск кратчайшего пути методом Дейкстры и методом Флойда-Уоршала. Провести сравнительные характкристики; i) определить минимальноем остовное дерево методом Крускала и методом Прима. Провести сравнительные характкристики.
1. 3. 5. 7. 9. 11. 13.
15.
Глава 5. Алгоритмы сортировок Сортировка выбором
Один из самых простых алгоритмов сортировки работает следующим образом. Сначала отыскивается наименьший элемент массива, затем он меняется местами с элементом, стоящим первым в сортируемом массиве. Далее, находится второй наименьший элемент и меняется местами с элементом, стоящим вторым в исходном массиве. Этот процесс продолжается до тех пор, пока весь массив не будет отсортирован. Изложенный метод называется сортировкой выбором, поскольку он работает по принципу выбора наименьшего элемента из числа неотсортированных. На рис. 1 представлен пример работы этого метода.
Рис.1. Пример работа сортировки выбором
В этом примере первый проход не дал результата, поскольку слева от А в массиве нет элемента, меньшего А. На втором проходе другой элемент А оказался наименьшим среди оставшихся, поэтому он меняется местами с элементом S, занимающим вторую позицию. Далее, на третьем проходе, элемент Е, находящийся в середине массива, меняется местами с О, занимающим третью позицию; затем, на четвертом проходе, еще один элемент Е меняется местами с R, занимающим четвертую позицию и т.д. Для каждого i от I до г-1 поменять местами элемент a[i] с минимальным элементом в последовательности a[i],...,a[r],. По мере продвижения индекса i слева направо, элементы слева от него занимают свои окончательные позиции в массиве (дальнейшим перемещениям они не подлежат), таким образом, массив будет полностью отсортирован, когда i достигнет его правого конца. Недостаток сортировки выбором заключается в том, что время ее выполнения лишь в малой степени зависит от того, насколько упорядочен исходный массив. Процесс нахождения минимального элемента за один проход массив дает очень мало сведений о том, где может находиться минимальный элемент на следующем проходе этого массива. На сортировку почти отсортированного массива требуется столько же времени, сколько и на сортировку массива, упорядоченного случайным образом!
Сортировка вставками
Метод сортировки заключается в том, что отдельно анализируется каждый конкретный элемент, который затем помещается в надлежащее место среди других, уже отсортированных элементов. Следует позаботиться о том, чтобы освободить место для вставляемого элемента путем смещения больших элементов на одну позицию вправо, после чего на освободившееся место помещается вставляемый элемент. Как и в случае сортировки выбором, элементы, находящиеся слева от текущего индекса, отсортированы в соответствующем порядке, тем не менее, они еще не занимают свои окончательные позиции, ибо могут быть передвинуты с целью освобождения места под меньшие элементы, которые обнаруживаются позже. Массив будет полностью отсортирован, когда индекс достигнет правой границы массива.
Рис.2. Пример работа сортировки вставками
Во время первого прохода сортировки вставками элемент S, занимающий вторую позицию, больше А, так что трогать его не надо. На втором проходе, когда в третьей позиции встречается элемент О, он меняется местами с S, так что последовательность становится АО S отсортированной и т.д.
Пузырьковая сортировка
Метод сортировки, который многие обычно осваивают раньше других из-за его исключительной простоты, называется пузырьковой сортировкой (bubble sort), в рамках которой выполняются следующие действия: проход по массиву с обменом местами соседних элементов, нарушающих заданный порядок, до тех пор, пока массив не будет окончательно отсортирован. Предположим, что мы всегда передвигаемся по массиву справа налево. Если удается обнаружить минимальный элемент на первом проходе, он меняется местами с каждым элементом, стоящим от него слева, и, в конце концов, этот элемент помещается в позицию на левой границе массива. Затем на втором проходе в соответствующую позицию устанавливается второй по величине элемент и т.д. Таким образом, вполне достаточно выполнить N проходов, т.е., пузырьковую сортировку можно рассматривать как один из видов сортировки выбором, хотя при этом для помещения каждого элемента в соответствующую позицию приходится выполнять больший объем действий. В общем случае пузырьковый метод обладает несколько меньшим быстродействием. В процессе пузырьковой сортировки элементы с малыми значениями устремляются влево. Поскольку сортировка производится в направлении справа налево, каждый элемент меняется местами с элементом слева до тех пор, пока не будет обнаружен элемент с меньшим значением. На первом проходе Е меняется местами с L, Ри М, пока не остановится справа от А; далее уже А продвигается к началу массива, пока не остановится перед другим А, который уже занимает окончательную позицию, i-й по величине элемент устанавливается в свое окончательное положение после i-ого прохода, как и в случае сортировки выбором, но при этом и другие элементы также приближаются к своим окончательным позициям.
Быстрая сортировка
Алгоритм быстрой сортировки обладает привлекательными особенностями: он принадлежит к категории обменных (in-place) сортировок (т.е., требует всего лишь небольшого вспомогательного стека), на выполнение сортировки N элементов в среднем затрачивается время, пропорциональное N log N и для него характерны исключительно короткие внутренний циклы. Его недостатком является то, что он неустойчив, для его выполнения в наихудшем случае требуется N2 операций, он хрупок в том смысле, что даже простая ошибка в реализации может пройти незамеченной и вызвать ошибки в работе алгоритма на некоторых видах массивов. Быстрый метод сортировки функционирует по принципу "разделяй и властвуй". Он делит сортируемый массив на две части, затем сортирует эти части независимо друг от друга. Суть метода заключается в процессе разбиения массива, который переупорядочивает массив таким образом, что выполняются следующие условия: Элемент a[i] для некоторого i занимает свою окончательную позицию в массиве. Ни один из элементов a[i],..., a[i-l] не превышает a[i]. Ни один из элементов a[i+l],..., а[г] не является меньшим a[i]. Быстрая сортировка представляет собой рекурсивный процесс разбиения массива на части: мы разбиваем его, помещая некоторый (разделяющий) элемент в свою окончательную позицию и выполняем перегруппировку массива таким образом, что элементы, меньшие по значению, остаются слева от разделяющего элемента, а элементы, большие по значению, — справа. Далее мы рекурсивно сортируем левую и правую части массива. Конечным результатом такого вида сортировки является полностью отсортированный массив. Разбиение осуществляется с использованием следующей стратегии. Прежде всего, в качестве разделяющего элемента произвольно выбирается элемент а[r], лучше чтобы r был ближе к середине — он сразу займет свою окончательную позицию. Далее начинается просмотр с левого конца массива, который продолжается до тех пор, пока не будет найден элемент, превосходящий по значению разделяющий элемент, затем выполняется просмотр, начиная с правого конца массива, который продолжается до тех пор, пока не отыскивается элемент, который по значению меньше разделяющего. Оба элемента, на которых просмотр был прерван, очевидно, находятся не на своих местах в разделенном массиве, и потому они меняются местами. Мы продолжаем дальше в том же духе, пока не убедимся в том, что слева от левого указателя не осталось ни одного элемента, который был бы больше по значению разделяющего, и ни одного элемента справа от правого указателя, которые были бы меньше по значению разделяющего элемента.
Листинг: Алгоритм быстрой сортировки
// Шаблон quicksort задает рекурсивную функцию сортировки // элементов массива методом быстрой сортировки. // - Key - класс, задающий тип элементов массива; // - array - упорядочиваемый массив; // -.low, high - индексы, задающие диапазон сортировки. template <class Кеу> void quicksort(Key * array, int low, int high) { // Предполагается, что в начале работы low <= high // В результате сортировки получается упорядоченный фрагмент // массива в диапазоне от low до high int pLow = low, pHigh - high; // указатели концов фрагмента массива Key elem = array[low]; // выбранный произвольный элемент while (pLow!= pHigh) { // 1. Просмотр элементов массива снизу
while (pHigh > pLow && array[pHigh] >= elem) pHigh--; if (pHigh > pLow) { array[pLow] =array[pHigh]; // Обмен местами элементов // 2. Просмотр элементов массива "сверху" while (pLow < pHigh && array[pLow] <= elem) pLow++; array[pHigh] = array [pLow]; // Еще один обмен } } // Теперь указатели pLow и pHigh столкнулись, массив разделен, array[pLow] = elem; // Далее следуют рекурсивные вызовы функции для двух половинок if (pLow - low > 1) quickSort<Key>(array, low, pLow-1); if (high - pHigh > 1) quickSort<Key>(array, pHigh+1, high); }
Сортировка слиянием
Рассматривается сортировка слиянием (mergesort), которая является дополнением быстрой сортировки в том, что она состоит из двух рекурсивных вызовов с последующей процедурой слияния. Одним из наиболее привлекательных свойств сортировки слиянием является тот факт, что она сортирует массив, состоящий из N элементов, за время, пропорциональное NlogN, независимо от характера входных данных. Сортировка слиянием — это устойчивая сортировка, и данное обстоятельство склоняет чашу весов в ее пользу в тех приложениях, в которых устойчивость имеет важное значение. Другое свойство сортировки слиянием, которое приобретает важное значение в некоторых ситуациях, является тот факт, что сортировка слиянием обычно реализуется таким образом, что она осуществляет, в основном, последовательный доступ к данным (один элемент за другим). Имея два упорядоченных входных массива, их можно объединить в один упорядоченный выходной массив просто отслеживая наименьший элемент в каждом массиве и входя в цикл, в котором меньший из двух элементов, наименьших в своих массивах, переносится в выходной массив; процесс продолжается до тех пор, пока оба входных массива не будут исчерпаны.
Листинг: Алгоритм сортировки слиянием //------------------------------------------------------------- // Шаблон move задает вспомогательную функцию, которая просто // переносит элементы массива из одного фрагмента массива // в другой фрагмент того же самого или другого массива. // - Key - класс, задающий тип элементов массива; // - src - исходный фрагмент массива; // - sLow, sHigh - индексы, задающие диапазон в исходном массиве; // - dst - результирующий фрагмент массива; // - dLow - индекс, задающий нижнюю границу результирующего массива. //------------------------------------------------------------- template <class Кеу> void move(Key * src, int sLow, int sHigh, Key * dst, int dLow) { for (int pSrc = sLow, pDst = dLow; pSrc <= sHigh;) { dst[pDst++] = src[pSrc++]; }} //------------------------------------------------------------- // Шаблон mergeSort задает функцию сортировки элементов // массива методом последовательного слияния. // - Key - класс, задающий тип элементов массива; // - array - упорядочиваемый массив; // - low, high - индексы, задающие диапазон сортировки. //------------------------------------------------------------- template <class Кеу> void mergeSort(Key * array, int low, int high) { // Предполагается, что в начале работы low <= high // В результате сортировки получается упорядоченный фрагмент // массива в диапазоне от low до high int n = high - low +1; // Длина массива int frag = n; // Число упорядоченных фрагментов int len = 1; // Длина сливаемых фрагментов Key * source = array, // Массив, из которого происходит слияние * dest = new Key[n]; // Массив, в который происходит слияние int sourceLow = low, // Нижняя граница индексов массива-источника destLow = 0; // Нижняя граница индексов массива-назначения while (frag > 1) { // Один шаг цикла слияния состоит в попарном слиянии фрагментов // исходного массива и переносе оставшихся неслитыми элементов // из исходного массива в результирующий. // Индексы pSource и pDest задают нижние границы этих массивов, int pSource = sourceLow, pDest = destLow; do { int nextSource =min(pSource + 2*len, sourceLow + n); // Выполняем слияние двух фрагментов или // перенос последнего оставшегося фрагмента if (nextSource > pSource + len) { merge<Key>(source, pSource, pSource+len-1, source, pSource+len, nextSource-1, dest, pDest); } else { move<Key>(source, pSource, nextSource-1, dest, pDest); } pSource = nextSource; pDest += 2*len; } while (pSource < sourceLow+n); len*= 2; // Длина фрагментов увеличивается вдвое frag = (frag+l)/2; // Число фрагментов уменьшается вдвое // Переставляем местами массивы источника и назначения: Key * tempArray = dest; dest =source; source = tempArray; int tempLow = destLow; destLow = sourceLow; sourceLow = tempLow; } // Если в конце работы результат оказался не на месте, //то организуется его перенос в исходный массив if (source!= array) { move<Key>(source, sourceLow, sourceLow+n-1, dest, destLow); }} Пирамидальная сортировка
Итак, мы постепенно переходим от более-менее простых к сложным, но эффективным методам. В качестве некоторой прелюдии к основному методу, рассмотрим перевернутую сортировку выбором. Во время прохода, вместо вставки наименьшего элемента в левый конец массива, будем выбирать наибольший элемент, а готовую последовательность строить в правом конце. Пример действий для массива a[0]... a[7]: 44 55 12 42 94 18 06 67 исходный массив 44 55 12 42 67 18 06 |94 94 <-> 67 44 55 12 42 06 18 |67 94 67 <-> 06 44 18 12 42 06 |55 67 94 55 <-> 18 06 18 12 42 |44 55 67 94 44 <-> 06 06 18 12 |42 44 55 67 94 42 <-> 42 06 12 |18 42 44 55 67 94 18 <-> 12 06 |12 18 42 44 55 67 94 12 <-> 12Вертикальной чертой отмечена левая граница уже отсортированной(правой) части массива. Итак, назовем пирамидой(Heap) бинарное дерево высоты k, в котором · все узлы имеют глубину k или k-1 - дерево сбалансированное. · при этом уровень k-1 полностью заполнен, а уровень k заполнен слева направо, т.е форма пирамиды имеет приблизительно такой вид: · выполняется "свойство пирамиды": каждый элемент меньше, либо равен родителю. Как хранить пирамиду? Наименее хлопотно - поместить ее в массив.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.92.58 (0.01 с.) |



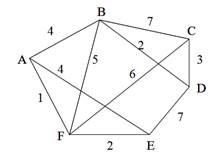 2.
2. 
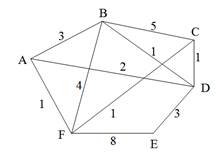 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 
 14.
14. 
 16.
16.