Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции поиска и включения элемента в деревоСтр 1 из 10Следующая ⇒
Содержание Глава 1. Основные операции при работе с деревьями. 4 1.1. Определение глубины дерева. 5 1.2. Операции поиска и включения элемента в дерево. 5 1.3. Оптимизация поиска в дереве. 6 1.3.1. Обходы дерева с нумерацией вершин. 7 1.4. Поиск и включение в двоичное дерево. 8 Контрольные вопросы.. 9 Задания для практической работы.. 9 Глава 2. Сбалансированные двоичные деревья. 14 2.1. Преобразование двоичного дерева в лозу. 14 2.2. Преобразование лозы в сбалансированное двоичное дерево. 15 Контрольные вопросы.. 17 Задания для практической работы.. 17 Глава 3. Жадные алгоритмы.. 18 3.1. Понятие жадного алгоритма. 18 3.2. Алгоритм Хаффмана. 18 Контрольные вопросы.. 20 Задания для практической работы.. 21 Глава 4. Графы.. 22 4.1. Алгоритмы представления графа. 22 4.1.1. Представление графа в виде массива. 23 4.1.2. Представление графа в виде матрицы смежности. 24 4.1.3. Представление графа в виде связанного списка. 26 4.1.4. Представление графа в виде списка дуг. 29 4.1.5. Преобразования структур графа. 31 4.2. Обходы в графах. 32 4.3. Определение путей и контуров Эйлера. 35 4.4. Поиск кратчайших путей. 37 4.4.1. Алгоритм Э. Дейкстры. 38 4.4.2. Алгоритм Флойда — Уоршалла. 40 4.5. Определение остовных деревьев. 41 4.5.1. Алгоритм Крускала. 42 4.5.2. Алгоритм Прима. 46 Контрольные вопросы.. 49 Задания для практической работы.. 49 Глава 5. Алгоритмы сортировок. 52 5.1. Сортировка выбором.. 52 5.2. Сортировка вставками. 52 5.3. Пузырьковая сортировка. 53 5.4. Быстрая сортировка. 54 5.5. Сортировка слиянием.. 55 5.6. Пирамидальная сортировка. 57 Контрольные вопросы.. 61 Задания для практической работы.. 61 Глава 6. Алгоритмы поиска. 62 6.1. Последовательный поиск. 62 6.2. Двоичный поиск. 62 6.3. Работа со словарем. Иоиск и вставка. Хеширование. 62 6.4. Поиск подстроки в строке. 69 6.4.1. Алгоритм прямого поиска подстроки в строке. 69 6.4.2. БМ-поиск (Боуера–Мура) 71 6.4.3. КМП-поиск (Кнута–Мориса и–Пратта) 74 Контрольные вопросы.. 79 Задания для практической работы.. 79
К основным операциям работы с деревьями относятся: а) поиск элемента в дереве. Операция заключается в прохождении узлов дерева в одном из рассмотренных выше порядке. При прохождении дерева поиска достаточно пройти только то поддерево, которое возможно содержит искомый элемент;
б) включение элемента в дерево. Операция заключается в добавлении листа (исключая сбалансированное дерево – включение элемента в сбалансированное дерево приводит, как правило, к его перестройке) в какое-то поддерево, если такого элемента нет в исходном дереве. При включении нового элемента в дерево поиска лист добавляется в то поддерево, в котором не нарушается отношение порядка; в) удаление элемента из дерева. Операция заключается в изменении связей между дочерними и родительскими, по отношению к удаляемому, элементами (исключая сбалансированное дерево – удаление элемента из сбалансированного дерева приводит, как правило, к его перестройке); здесь необходимо рассматривать три случая: удаление листа (см. рис.1.а), удаление элемента с одним потомком (см. рис.1.б), удаление элемента с двумя потомками (см. рис.1.в).
Рис. 1. Случаи удаления листа дерева
При удалении элемента степени 2 из дерева поиска изменять связи необходимо так, чтобы не нарушалось установленное в дереве отношение порядка. Лучшим вариантом в этом случае будет перемещение на место удаляемого элемента либо самого правого листа из левого поддерева удаляемого элемента, либо самого левого листа из правого поддерева удаляемого элемента; г) сравнение деревьев (проверка деревьев на равенство). Операция заключается в прохождении обоих деревьев в одном порядке до тех пор, пока либо не будут пройдены оба дерева, либо одно из них, либо соответствующие элементы окажутся не равными, либо в одном из деревьев не будет обнаружено отсутствие соответствующего элемента. Только в случае равенства деревьев оба дерева будут пройдены одновременно; д) копирование дерева. Операция заключается в прохождении исходного дерева и построении нового дерева с элементами, информационные поля которых равны информационным полям соответствующих элементов исходного дерева. Далее рассмотрим операции поиска и включения элемента в дерево. Остальные операции можно выполнить на основе работы алгоритмов поиска и включения элемента в дерево.
Определение глубины дерева
При определении минимальной (максимальной) длины ветви дерева каждая вершина должна получить значения минимальных длин ветвей от потомков, выбрать из них наименьшую и передать предку результат, увеличив его на 1 - " добавить себя". struct tree{int val;tree *p[4];};//---- Определение ветви минимальной длиныint MinLnt(tree *q){if (q==NULL) return 0;int min= MinLnt(q->p[0]); for (int i=1; i< 4; i++){ int x=MinLnt(q->p[i]); if (x < min) min=x;}return min+1;}Для отслеживания процесса " погружения" достаточно дополнительной переменной, которая уменьшает свое значение на 1 при очередном рекурсивном вызове. //------Включение вершины в дерево на заданную глубинуint Insert(tree *ph, int v, int d) { // d - текущая глубина включенияif (d == 0) return 0; // Ниже не просматриватьfor (int i=0; i< 4; i++) if (ph->p[i] == NULL){ tree *pn=new tree; pn->val=v; for (int j=0; j< 4; j++) pn ->p[j]=NULL; ph->p[i]=pn; return 1; }else if (Insert(ph->p[i], v, d-1)) return 1; // Вершина включенаreturn 0; }Для включения простейшим способом нового значения в дерево в ближайшее в корню место достаточно соединить две указанные функции вместе. void main(){ tree PH={ 1,{NULL,NULL,NULL,NULL} };for (int i=0; i< 100; i++) Insert(& PH, rand(20), MinLnt(& PH));}Оптимизация поиска в дереве
Основное свойство дерева соответствует пословице " дальше в лес - больше дров". Точнее, количество просматриваемых вершин от уровня к уровню растет в геометрической прогрессии. Если известен некоторый критерий частоты использования различных элементов данных (например, более короткие строки используются чаще, чем длинные), то в соответствии с ним можно частично упорядочить данные по этому критерию с точки зрения их " близости" к корню: в нашем примере в любом поддереве самая короткая строка находится в его корневой вершине. Алгоритм поиска может ограничить глубину просмотра такого дерева. //--- Дерево оптимизацией: короткие ключи ближе к началуstruct dtree{char *key; // Ключевое словоvoid *data; // Искомая информацияdtree *p[4]; }; // Потомкиvoid *find(dtree *q, char *keystr) // Поиск по ключу{ void *s;if (q==NULL) return NULL;if (strcmp(q->key,keystr)==0) return q->data; // Ключ найденif (strlen(keystr)<strlen(q->key)) return NULL; // Короткие строки - ближе к корнюfor (int i=0; i< 4; i++) if ((s=find(q->p[i],keystr))!=NULL) return s;return NULL; }Функция включения в такое дерево ради сохранения свойств должна в каждой проходимой ею вершине рекурсивно " вытеснять" более длинную строку в поддерево и заменять ее на текущую (новую), более короткую. Задания для практической работы Создать класс операций по работе с деревом. Программа должна содержать функцию обхода дерева с выводом его содержимого, функцию добавления вершины дерева (ввод), а также указанную в варианте функцию. 1. Вершина дерева содержит указатель на строку. Строки в дереве не упорядочены. Функция включает вершину в дерево с новой строкой в ближайшее свободное к корню дерева место. (В результате дерево будет сбалансированным). Для исключения полного обхода в каждую вершину дерева поместить длину его минимальной ветви и корректировать его в процессе включения во всех проходимых вершинах. 2. Вершина двоичного дерева содержит массив целых и два указателя на правое и левое поддерево. Массив целых в каждом элементе упорядочен, дерево в целом также упорядочено. Функция включает в дерево целую переменную с сохранением упорядоченности.
3. Вершина двоичного дерева содержит указатель на строку и указатели на правое и левое поддерево. Строки в дереве упорядочены по возрастанию. Написать функций включения строки и получения указателя на строку по заданному номеру, который она имеет в упорядоченной последовательности обхода дерева. 4. Элемент дерева содержит либо данные (строка ограниченной длины), либо указатели на правое и левое поддеревья. Строки в дереве упорядочены. Написать функцию включения новой строки. (Обратить внимание на то, что элемент с указателями не содержит данных, и при включении новой вершины вершину с данными следует заменить на вершину с указателями).
5. Вершина дерева содержит целое число и массив указателей на поддеревья. Целые в дереве не упорядочены. Функция включает вершину в дерево с новой целой переменной в ближайшее свободное к корню дерева место. (То есть дерево должно иметь ветви, отличающиеся не более чем на 1).
6. Вершина дерева содержит два целых числа и три указателя на поддеревья. Данные в дереве упорядочены. Написать функцию включения нового значения в дерево с сохранением упорядоченности.
7. Вершина дерева содержит указатель на строку и N указателей на потомков. Функция помещает строки в дерево так, что строки с меньшей длиной располагаются ближе к корню. Если новая строка " проходит" через вершину, в которой находится более длинная строка, то новая занимает место старой, а алгоритм включения продолжается для старой строки. Функция включения выбирает потомка минимальным количеством вершин в поддереве. 8. Вершина дерева содержит либо 4 целых значения, либо 2 указателя на потомков, причем концевые вершины содержат данные, а промежуточные - указатели на потомков. Естественная нумерация значений производится при обходе концевых вершин слева направо. Разработать функции получения и включения значения в дерево по логическому номеру.
9. Вершина дерева содержит N целых значений и два указателя на потомков. Запись значений производится таким образом, что меньшие значения оказываются ближе к корню дерева (то есть все значения в поддеревьях больше самого большого значения у предка). Разработать функции включения и поиска данных в таком дереве. Если новое значение " проходит" через вершину, в которой находится большее, то оно замещает большее значение, а для последнего алгоритм включения. Функция включения выбирает потомка максимальным значением в поддереве.
10. Выражение, содержащее целые константы, арифметические операции и скобки, может быть представлено в виде двоичного дерева. Концевая вершина дерева должна содержать значение константы. Промежуточная - код операции и указатели на правый и левый операнды - вершины дерева. Функция получает строку, содержащую выражение, и строит по ней дерево. Другая функция производит вычисления по полученному дереву. 11. Вершина дерева содержит указатель на строку и динамический массив указателей на потомков. Размерность динамического массива в корневой вершине - N, на каждом следующем уровне - в 2 раза больше. Функция при включении строки создает вершину, наиболее близкую к корню. 12. Вершина дерева содержит динамический массив целых значений и два указателя на потомков. Значения в дереве не упорядочены. Размерность динамического массива в корневой вершине - N, на каждом следующем уровне - в 2 раза больше. Функция включает новое значение в свободное место в массиве ближайшей к корню вершины. 13. Вершина дерева содержит массив целых и два указателя на правое и левое поддерево. Значения в дереве не упорядочены. Естественная нумерация значений производится путем обхода дерева по принципу " левое поддерево - вершина - правое поддерево". Разработать функции включения и получения значения элемента по заданному логическому номеру. 14. Написать функцию, которая добавляет к бинарному дереву T новую вершину с элементом E (если ее не было в T). 15. Написать функцию, которая заменяет в дереве T значения всех отрицательных элементов вершин на их абсолютные величины (информационное поле вершины дерева T имеет тип Real). 16. Написать функцию, которая удаляет все вершины с одинаковыми элементами из непустого дерева T (разрешается использовать вспомогательную множественную структуру данных). 17. Написать функцию, которая удаляет из непустого бинарного дерева T вершины, содержащие максимальный и минимальный элемент (информационное поле вершины дерева имеет тип Real). 18. Написать функцию, которая удаляет из непустого дерева поиска T вершины, содержащие максимальный и минимальный элемент (информационное поле вершины дерева имеет тип Real). 19. Написать функцию, которая удаляет из непустого дерева все вершины с положительными элементами (информационное поле вершины дерева имеет тип Real). 20. Написать функцию, которая удаляет из непустого дерева поиска все вершины с отрицательными элементами (информационное поле вершины дерева имеет тип Real). 21. Написать функцию, которая определяет, входит ли вершина, содержащая информационное поле E, в заданное бинарное дерево дважды. 22. Написать функцию, которая проверяет, входит ли вершина, содержащая информационное поле E, в правое или левое поддерево заданного дерева поиска. 23. Написать функцию, которая проверяет совпадают ли элемент из самого левого листа непустого поиска дерева с элементом из самого правого листа того же дерева.
24. Установить, можно ли попасть из одной вершины бинарного дерева в другую, если двигаться по ветвям к листьям. 25. Установить, можно ли попасть из одной вершины дерева поиска в другую, если двигаться по ветвям к листьям. 26. Используя линейную скобочную запись дерева поиска, описать логическую функцию, проверяющую на равенство деревья поиска T1 и T2. 27. Написать с помощью линейной скобочной записи бинарного дерева функцию, проверяющую, входит ли вершина с элементом E в правое (левое) поддерево заданного бинарного дерева. 28. Два бинарных дерева называются изоморфными, если можно отобразить одно из них в другое, изменив порядок сыновей его узлов. Распознать изоморфизм двух данных бинарных деревьев. 29. Описать функцию, которая определяет количество вхождений вершины с заданным элементом E в бинарное дерево. 30. Описать функцию, которая вычисляет сумму элементов всех вершин заданного непустого дерева поиска (информационное поле вершины дерева имеет тип Real). 31. Описать функцию, которая определяет максимальную глубину непустого дерева, т.е. количество ветвей в самом длинном из путей от корня дерева до листьев. 32. Определить глубину (высоту) непустого дерева поиска, используя функцию определения пути от данной вершины до корня. 33. Используя линейную скобочную запись дерева, описать функцию, которая определяет максимальную глубину непустого бинарного дерева. 34. Описать функцию, которая подсчитывает количество вершин на k-ом уровне непустого дерева поиска (корень - вершина 0-го уровня). 35. Написать функцию, которая определяет количество вхождений элемента E в информационные поля вершин левого поддерева заданного бинарного дерева. 36. Написать функцию, которая вычисляет среднее арифметическое всех элементов заданного непустого дерева (информационное поле вершины дерева имеет тип Real). 37. Написать функцию, которая находит в заданном непустом бинарном дереве длину (количество ветвей) пути от корня до ближайшей вершины с заданным элементом E. 38. Определить суммарный путь данного дерева поиска, используя функцию определения пути от данной вершины до корня. 39. Используя линейную скобочную запись дерева, написать функцию, которая находит содержимое информационного поля самого левого (правого) листа непустого дерева поиска. 40. Используя линейную скобочную запись дерева, написать функцию, которая определяет количество вхождений вершины с элементом E в левое поддерево заданного бинарного дерева. 41. Используя линейную скобочную запись дерева, написать функцию, которая находит в заданном непустом бинарном дереве длину (количество ветвей) пути от корня до вершины с заданным элементом E. 42. Написать функцию, которая выбирает из непустого дерева поиска все разные английские буквы (информационное поле вершины дерева имеет тип Char). 43. Написать функцию, которая определяет максимальный элемент из всех листьев непустого бинарного дерева (информационное поле вершины дерева имеет тип Integer). 44. Написать процедуру, которая выводит на экран содержимое информационных полей всех внутренних вершин бинарного дерева. 45. Выписать все вершины дерева поиска, находящиеся на заданном уровне k (k=0,1,2,...), используя функцию определения пути от данной вершины до корня.
Задания для практической работы
Требуется: - запрограммировать алгоритм балансировки дерева; - количество вершин лозы определяется случайно в диапазоне от 7 до 31; - каждое перестроение выводить на экран.
Глава 3. Жадные алгоритмы
Понятие жадного алгоритма Жадный алгоритм (англ. Greedy algorithm) — алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская что конечное решение также окажется оптимальным. Общего критерия оценки применимости жадного алгоритма для решения конкретной задачи не существует, однако, для задач, решаемых жадными алгоритмами характерны две особенности: во-первых, к ним применим Принцип жадного выбора; во-вторых, они обладают свойством Оптимальности для подзадач. Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных выборов даёт глобально оптимальное решение. В типичном случае доказательство оптимальности следует такой схеме: Сначала доказывается, что жадный выбор на первом шаге не закрывает пути к оптимальному решению: для всякого решения есть другое, согласованное с жадный выбором и не худшее первого. Затем показывается, что подзадача, возникающая после жадного выбора на первом шаге, аналогична исходной, и рассуждение завершается по индукции. Говорят, что задача обладает свойством оптимальности для подзадач, если оптимальное решение задачи содержит в себе оптимальные решения для всех её подзадач. Например, в задаче о выборе заявок можно заметить, что если A — оптимальный набор заявок, содержащий заявку номер 1, то Пример 1: Размен монет. Условие: Монетная система некоторого государства состоит из монет достоинством a 1 = 1 < a 2 <... < an. Требуется выдать сумму S наименьшим возможным количеством монет. Жадный алгоритм решения этой задачи таков. Берётся наибольшее возможное количество монет достоинства an: Для данной задачи жадный алгоритм не всегда даёт оптимальное решение. Например, сумму в 10 копеек монетами в 1, 5 и 6 коп. жадный алгоритм разменивает так: 6 коп. — 1 шт., 1 коп. — 4 шт., в то время как правильное решение — 2 монеты по 5 копеек. Тем не менее, на всех реальных монетных системах жадный алгоритм даёт правильный ответ.
Алгоритм Хаффмана Алгоритм Хаффмана (англ. Huffman) — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году доктором Массачусетского технологического института Дэвидом Хаффманом. Коды Хаффмана широко используются при сжатия информации (в типичной ситуации выигрыш может составить от 20% до 90% в зависимости от тина файла). Алгоритм Хаффмана находит оптимальные префиксы (коды символов), исходя из частоты использования этих символов в сжимаемом тексте, с помощью жадного выбора. Пусть в файле длины 100 000 известны частоты символов. Мы хотим построить двоичный код, в котором каждый символ представляется в виде конечной последовательности битов, называемой кодовым словом.
Таблица 1. Коды символов
При использовании равномерного кода, в котором все кодовые слова имеют одинаковую длину, на каждый символ (из шести имеющихся) надо потратить как минимум три бита, например, а — 000, b — 001,...,f — 101 (таб.1.). На весь файл уйдет 300 000 битов.
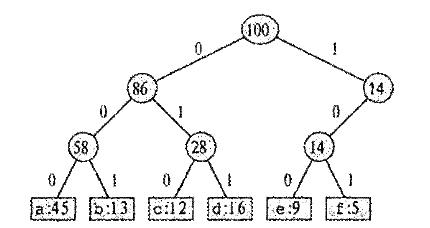
Рис.1. Представление равномерного кода в виде дерева Неравномерный код будет экономнее, если часто встречающиеся символы закодировать короткими последовательностями битов, а редко встречающиеся длинными.
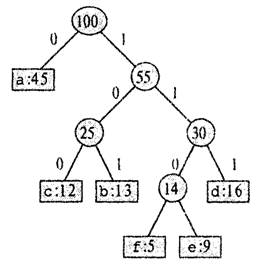
Рис.2. Представление неравномерного кода в виде дерева
. Один такой код показан на рис.2: буква а изображается однобитовой последовательностью 0, а буква f четырёхбитовой последовательностью 1 100. При такой кодировке на весь файл уйдёт (45- 1 + 13-3+ 12-3+ 16-3 + 9-1 +5-1) * 1000 = 221000 битов, что даёт около 25% экономии.
Этот метод кодирования состоит из двух основных этапов: 1. Построение оптимального кодового дерева. 2. Построение отображения код-символ на основе построенного дерева.
Общая схема построения дерева Хаффмана (рис.3): 1. Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа). 2. Из списка выберем 2 узла с наименьшим весом (под весом можно понимать частоту использования символа — чем чаще используется, тем больше весит). 3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов. 4. Добавим сформированный узел к списку. 5. Если в списке больше одного узла, то повторить 2-5.
Рис.3. Этапы построения дерева Хаффмана Контрольные вопросы 1. В чем принцип работы жадного алгоритма? 2. Какие типы задач можно решать с помощью жадного алгоритма? 3. Что понимается под методом Хаффмана? 4. Где применяется метод Хаффмана? 5. Как строится дерево Хаффмана? 6. Как вычислить размер исходного текста и сжатого? 7. Что является «префиксом»?
Задания для практической работы Задание состоит из нескольких этапов: 1. Получить у преподавателя индивидуальный текст для сжатия. 2. Создать программный модуль, который - из исходного текста получает список кодируемых символов; - Рассчитать размер несжатого файла; - С учетом полученных вероятностей, построить дерево Хаффмана; - Рассчитать размер сжатого файла. 3. Провести сравнительный анализ сжатия при разных характеристика исходного файла. Глава 4. Графы
В процессе обработки данных на компьютере часто приходится моделировать объекты сложной структуры, содержащие в качестве составных частей (элементов) объекты более простой структуры. Примерами таких структур являются— массивы, множества, списки и деревья. Иногда сложный объект состоит из некоторого множества элементов одного и того же типа, между которыми существуют определенные связи (отношения). В технике такие объекты часто называют сетями. Для моделирования сетей в математике служат объекты, называемые графами. Графом G называется пара множеств (V, E), где V— конечное множество элементов, называемых вершинами графа, а E— конечное множество упорядоченных пар е = (w, v), называемых дугами, где w, v— вершины. Говорят, что дуга е выходит из вершины w и входит в вершину v. Вершины w и v называют инцидентными дуге е, а дугу е — инцидентной вершинам w и v. В этом определении множество вершин V соответствует множеству узлов моделируемой сети, а множество дуг— связям между узлами. Определение, данное выше, отражает лишь структуру сети, но не характеристики ее отдельных узлов и связей. Если такие характеристики все же существенны, то рассматривают нагруженные графы, в которых с каждой вершиной или дугой (может быть, и с тем, и с другим) связана величина или несколько величин, называемых нагрузкой на граф. Формально говоря, нагрузку графа определяют функции: f: V->W1 g: E -> W2, где W1 и W2 представляют собой множества значений нагрузки вершин и дуг графа соответственно. Иногда при анализе графа неважно, какая из вершин w и v в дуге е = (w, v) первая, а какая вторая, т. е. пара (w, v) не упорядочена. В этом случае дугу е называют ребром, а весь граф называют неориентированным в отличие от ориентированного графа, задаваемого исходным определением. Разумеется, в этом случае бессмысленно говорить о том, из какой вершины ребро выходит и в какую вершину входит. Формально говоря, неориентированным графом называют такой граф, у которого наряду с любой дугой e1 = (u, v) имеется и противоположная дуга е2 — (v, u). Эта пара дуг и образует ребро е = <u, v> неориентированного графа.
Обходы в графах
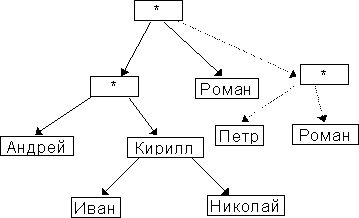
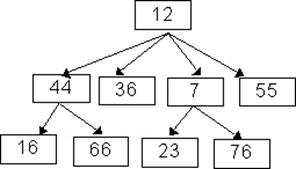
Как и в случае обхода деревьев, для графов существуют два основных класса обходов: обходы в глубину и обходы в ширину. Обходы в глубину пытаются каждый раз после прохождения некоторой вершины А выбрать в качестве следующей такую вершину В, в которую из вершины А ведет дуга. Таким образом, алгоритмы этого класса пытаются всегда двигаться вглубь графа, находя все новые не пройденные ранее вершины. Если таких непройденных вершин нет, то алгоритм возвращается к предыдущей, ранее пройденной вершине, и пытается найти очередную дугу, ведущую из нее в какую-либо другую еще не пройденную вершину. Если и таких вершин нет, то снова происходит откат назад, и так до тех пор, пока либо все вершины не будут пройдены, либо алгоритм вернется назад в вершину, выбранную в качестве исходной. Обходы в ширину пытаются, начав с некоторой вершины, в качестве очередных рассматривать только вершины, непосредственно связанные с исходной. Только после того, как все такие вершины будут рассмотрены, алгоритм будет пытаться рассматривать следующий слой вершин, непосредственно связанных с только что пройденными. Таким образом, алгоритм обхода в ширину последовательно рассматривает все более удаленные от исходной вершины до тех пор, пока либо все вершины не будут пройдены, либо не останется больше вершин, достижимых из исходной. Рассмотрим в качестве примера граф, изображенный на рис. 3. Этот граф содержит 9 вершин и 12 дуг. Он состоит из двух компонент связности, так что заведомо не удастся обойти его весь, выбрав некоторую вершину в качестве исходной и проходя только по направлениям дуг. Тем не менее если сначала выбрать в качестве исходной вершины вершину 1, то все остальные вершины одной компоненты связности из нее будут достижимы, так что по крайней мере эта компонента связности будет пройдена до того, как потребуется вновь выбирать начальную вершину. Тем же свойством обладают и все остальные вершины графа, кроме вершины 7. Если выбрать ее в качестве начальной вершины для обхода, то будет пройдена только она сама, а потом потребуется вновь выбирать некоторую вершину в качестве начальной для обхода остальных. Если в качестве алгоритма обхода взять алгоритм обхода в глубину, причем договориться, что из всех возможных альтернатив он всегда выбирает проход к вершине с наименьшим номером, то получится следующий порядок обхода вершин графа: 0; 1; 4; 6; 3; 7; 2; 8; 5 Порядок обхода в ширину в данном случае отличается от порядка обхода в глубину незначительно: 0; 1; 4; 6; 7; 3; 2; 8; 5 это получается потому, что граф, выбранный для примера, очень небольшой. Обычно в случае больших графов порядки обхода отличаются весьма существенно.
На рис. 3 также изображена логическая структура графа. Для того чтобы яснее представить себе работу алгоритмов обхода, необходимо хорошо представлять также и физическую структуру памяти соответствующего объекта. В представлении графа рис. 3 в виде L-графа имеются 9 списков дуг (для каждой вершины существует список исходящих из нее дуг). На этом рисунке изображен массив списков дуг (около каждого элемента массива показан номер соответствующей вершины графа). Дуги представлены прямоугольниками, содержащими номер той вершины, в которую дуга входит. В качестве первого примера рассмотрим внешний итератор вершин графа при обходе в глубину. Для того чтобы перейти от текущей вершины графа к следующей, итератор должен, во-первых, запоминать, какие из вершин уже пройдены или не пройдены, а во-вторых, для быстрого возврата к предыдущей вершине помнить последовательность дуг на пути из выбранной начальной вершины в текущую. Эту последовательность дуг будет удобно представляться в виде стека, элементами которого будут содержать информацию, необходимую для возврата по дугам. Пусть алгоритм выбрал в качестве начальной вершину с номером 0. Тогда обход графа начнется в ситуации, приведенной в первой строке табл.1. Таблица 1. Последовательность состояний при обходе графа в глубину
Итератор обходит текущую вершину и выбирает следующую вершину из числа тех, в которые ведут дуги из текущей вершины. После первого шага ситуация будет такой, как показано в строке 2 табл. 1. Пройденная на этом шаге дуга 0-1 помещается в стек. Следующие три шага выполняются аналогично, а последовательное изменение ситуации показано в табл. 1 в строках 3-5. В тот момент, когда текущей стала вершина 3, оказывается, что единственная дуга, ведущая из нее, ведет в уже пройденную вершину 0, поэтому следует, используя стек, вернуться на шаг назад в вершину 6 и попытаться найти следующую вершину по одной из дуг, ведущих из этой вершины. Поскольку новых дуг, ведущих из вершины 6, тоже больше нет, то делаем еще шаг назад к вершине 4. Теперь уже находится дуга, ведущая из этой вершины в еще не пройденную вершину 7, так что после прохода по соответствующей дуге образуется новая ситуация, показанная в табл. 1 в строке 6. После прохождения вершины 7 оказывается, что больше нет дуг, ведущих в еще не пройденные вершины ни из вершины 7, ни из всех предыдущих вершин на пути в эту вершину. В строке 7 таблицы показана ситуация, возникшая после проверки всех этих дуг. Теперь можно снова выбрать произвольно одну из непройденных вершин, скажем, вершину 2, и далее алгоритм последовательно переберет вершины 2, 8 и 5 так, как показано в строках 8—11. Теперь все вершины графа оказываются пройденными. Для обходов в ширину приведем два способа обхода— с помощью внешнего и внутреннего итераторов, которые, схематично описанного ниже. Выберем произвольную вершину графа и начнем обход с этой вершины. В процессе работы алгоритма будем делить все вершины графа на три класса: - пройденные вершины ("черные"); - вершины, которые будут пройдены на следующем шаге алгоритма ("серые"); - и все остальные непройденные вершины ("белые"). В начальный момент работы выбранная исходная вершина помещается в множество "серых" вершин, а все остальные вершины будут пока "белыми". Один шаг работы алгоритма состоит в том, что берутся все "серые" вершины, проходятся (и помещаются во множество "черных" вершин), затем находятся все "белые" вершины, в которые ведут дуги из только что пройденных вершин, и все найденные вершины перекрашиваются в серый цвет, т. е. помещаются в множество "серых" вершин. Если "серых" вершин больше нет, то это означает, что пройдены уже все вершины, достижимые из исходной. Если при этом в графе еще остались непройденные "белые" вершины, можно снова выбрать одну из них в качестве исходной и повторить работу алгоритма. На практике множество "серых" вершин можно организовать в виде очереди, тогда вершины из очереди можно брать по одной из головы очереди, а новые вершины, в которые ведут из нее дуги, сразу же помещать в конец очереди. Поиск кратчайших путей Путем в графе называют чередующуюся последовательность вершин и дуг v1, e1, v2, e2,... vn-1 en-1, vn, в которой каждый элемент vi— вершина графа, а каждый элемент еi — дуга графа, ведущая из предыдущей вершины vi в следующую вершину vi+1|. Говорят, что такой путь соединяет вершину v1 с вершиной vn. Чаще всего рассматриваются простые пути, т. е. такие, в которых нет повторяющихся вершин, кроме, быть может, совпадения первой и последней вершины. В случае такого совпадения путь называется замкнутым или циклом. Среди характеристик пути чаще всего рассматривается его длина— количество дуг в этом пути. Иногда с каждой дугой связывается некоторое число, которое можно интерпретировать как длину этой дуги. Граф в этом случае называется нагруженным, а длиной пути в нагруженном графе будет называться сумма длин входящих в этот путь дуг. Самая простая задача поиска кратчайшего пути в графе состоит в следующем. Пусть заданы две вершины — начальная и конечная. Известно, что имеется по крайней мере один путь, по которому можно пройти, чтобы попасть из начальной вершины в конечную. Требуется указать один из таких путей. Более интересная задача состоит в том, чтобы найти кратчайший путь между двумя вершинами при условии, что каждая дуга имеет определенную длину, так что мерой такого расстояния будет не количество дуг на кратчайшем пути, а суммарная длина пути. Алгоритм Э. Дейкстры.
Опишем алгоритм нахождения такого пути при условии, что длины всех дуг неотрицательны. Этот алгоритм был предложен и опубликован Э. Дейкстрой (Е. W. Dijkstra), поэтому и носит его имя. Алгоритм поиска кратчайшего пути в этом случае несколько напоминает алгоритм обхода графа в ширину и состоит в следующем. Будем рассматривать два множества: множество вершин, для которых уже известен кратчайший путь до них из начальной вершины (passed), и множество еще не исследованных вершин (notPassed). В начале работы первое множество будет пустым, а второе будет содержать все вершины графа. На каждом шаге работы алгоритма из второго множества в первое переводится одна вершина — та, расстояние до которой от исходной вершины минимально. Эту вершину будем называть пограничной (border).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.248.208 (0.161 с.) |


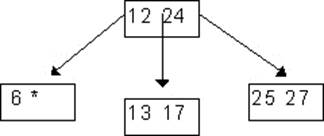

 — оптимальный набор заявок для меньшего множества заявок
— оптимальный набор заявок для меньшего множества заявок 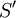 , состоящего из тех заявок, для которых
, состоящего из тех заявок, для которых 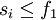 .
.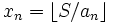 . Таким же образом получаем, сколько нужно монет меньшего номинала, и т. д.
. Таким же образом получаем, сколько нужно монет меньшего номинала, и т. д.