Представление графа в виде матрицы смежности

 

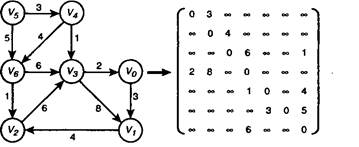
Еще один распространенный способ представления графа — это представление в виде матрицы смежности размером N * N (рис.1). B этой матрице в элементе с индексами (i,j) записывается информация о дугах, ведущих из вершины с номером i в вершину с номером j. В важном частном случае простого графа, т. е. графа, в котором каждая упорядоченная пара вершин соединена не более чем одной дугой, и отсутствуют дуги вида (u, u), элементы матрицы могут принимать значения 0 или 1 в зависимости от того, существует ли соответствующая дуга. Ясно, что такое представление самым тесным образом связано с представлением, описанным выше в определении класса setGraph.

Представление в виде матрицы смежности будем называть М-графом. Удобно связывать с матрицей смежности информацию о нагрузке на дуги. В этом случае элементом матрицы будет либо значение нагрузки на соответствующую дугу, либо некоторое стандартное значение, говорящее об отсутствии дуги.

Рис.1. граф и его представление в виде матрицы смежности

 

Если, например, граф моделирует транспортную сеть, в которой нагрузка на дугу представляет расстояние между пунктами, соединенными этой дугой, то признаком отсутствия дуги удобно сделать значение 0 или, напротив, максимально возможное целое, смотря по тому, что окажется более удобным в используемом алгоритме. В общем виде, если тип нагрузки представлен значениями класса W, то представление графа будет содержать двумерный массив значений класса W. Мы для простоты не будем интересоваться нагрузкой на дуги графа, таким образом, элементами матрицы, представляющей М-граф, могут быть просто логические значения.

 файл MatrixGraph.h   

#include "graph.h"

class MatrixGraph: public Graph {

bool **graph;

int vertexNumber;

 

public:

// Конструктор с параметром - количеством вершин графа.

MatrixGraph(int n);

 

// Количество вершин постоянно и содержится в поле vertexNumber

int vertexCount() const { return vertexNumber; }

 

// Остальные виртуальные функции, реализацию которых требуется

// предоставить при определении конкретного представления графа

void addArc(int from, int to);

bool hasArc(int from, int to) const;

};

 

файл MatrixGraph.cpp

#include "MatrixGraph.h"

 

// Реализация конструктора - заказ и инициализация памяти

// под двумерный массив логических значений

MatrixGraph::MatrixGraph(int n)

{

graph = new bool*[vertexNumber = n];

for (int i = 0; i < n; i++)

{

bool * row = graph[i] = new bool[n];

for (int j = 0; j < n; j++) {

row[j] = false; }

}

}

bool MatrixGraph::rhasArc(int from, int to) const 

{

if (from < 0 || from >= vertexNumber || to < 0 || to >= vertexNumber)

return false;                              // неправильно заданы номера вершин

return graph[from][to];

}

void MatrixGraph::addArc(int from, int to)

{

if (from < 0 || from >= vertexNumber || to < 0 || to >= vertexNumber)

return;                                           // невозможно добавить дугу

graph[from][to] =true;)

 

Поскольку представление M-графа очень близко к представлению S-графа, то и операции над M-графом выполняются практически с той же степенью эффективности, что и для S-графа. Удобными и эффективно реализуемыми операциями над M-графом являются операции проверки наличия дуги, значения ее нагрузки (в случае нагруженного графа), добавления и удаления дуг, изменения нагрузки.

Менее эффективными операциями будут операция подсчета или перебора дуг, инцидентных заданной вершине. Между тем во многих алгоритмах именно эта операция является самой часто используемой. Структура графа может меняться крайне редко, а вот исследоваться эта структура будет достаточно часто, причем инцидентность вершин и дуг чаще всего является главным предметом таких исследований. В этом случае представление графа в виде матрицы смежности будет неудобным.

Еще одно соображение. Если число вершин графа велико, то матрица смежности будет занимать достаточно много места. В то же время в графе количество дуг чаще всего существенно меньше NxN— размера матрицы, так что большинство элементов матрицы смежности будут пустыми.