Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Сбалансированные двоичные деревья
После каждой операции изменения дерева можно проводить балансировку дерева, которая позволяет минимизировать его высоту. При этом поиск по двоичному дереву будет требовать минимального времени. Балансировка позволяет также ускорить операции вставки и удаления узлов, которые тоже требуют проведения поиска. К сожалению, пока нет способа проведения быстрой балансировки дерева до его минимальной высоты. Тем не менее, балансировка является очень эффективным методом. Мы не можем провести балансировку дерева до его минимальной высоты, но, задав критерий "разбалансированности" дерева перед проведением очередной балансировки, можно приблизиться к этой минимальной высоте. В этом случае, хотя мы и не получаем дерева с минимально возможной высотой в каждый момент времени, тем не менее, находимся близко к минимуму. Алгоритм балансировки состоит из двух частей: 1. Дерево преобразуется в лозу. 2. Лоза перестраивается в сбалансированное дерево. Лоза (vine) — это левоассоциативное двоичное дерево. Она имеет следующий вид:
Рис.1. Левоассоциативное двоичное дерево – лоза
Главная лоза (рис.2) (main vine) — это левоассоциативное поддерево двоичного дерева.
Рис.2. Левоассоциативное поддерево двоичного дерева
На рисунке вершины главной лозы окрашены в белый цвет.
2.1. Преобразование двоичного дерева в лозу.
Мы проходим по дереву указателем p, начиная в корне дерева. Вспомогательный указатель q указывает на родителя p (поскольку мы строим левоассоциативное дерево, то p всегда является левым ребенком q). На каждом шаге возникает одна из двух возможных ситуаций: - Если у p нет правого ребенка, то эта часть дерева уже перестроена. p и q просто спускаются по дереву (приравниваются своим левым сыновьям). - Если у p есть правый ребенок (обозначим его r), тогда выполняется левый поворот относительно p:
Рис. 3. Выполнение левого поворот
На рисунке a, b и c обозначают поддеревья, которые могут быть пусты. После поворота устанавливаем указатель p на r.
2.2. Преобразование лозы в сбалансированное двоичное дерево.
Этот этап алгоритма более содержательный и поэтому менее очевидный. Поэтому сначала будет разобран простой пример, а потом будет дано его обобщение.
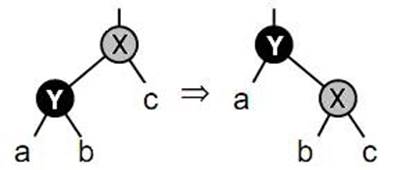
Пусть есть лоза, которая состоит из 2n-1 вершин для какого-либо натурального n. Для примера возьмем n=4, тогда лоза будет содержать 15 вершин. Преобразуем данную лозу в сбалансированное дерево за три операции перестроения. На первой операции пройдем по лозе сверху вниз, начиная в корне, и раскрасим каждую вершину соответственно в серый или черный цвет (условимся, что корень будет серого цвета). Затем возьмем каждую серую вершину, кроме самой нижней, сделаем ее правым ребенком черной вершины, являющейся ее левым ребенком. Т.е. выполним малый правый поворот относительно каждой серой вершины, кроме самой нижней (на рисунке 4 приведен пример малого правого поворота относительно вершины X).
Рис.4. Малый правый поворот относительно вершины X
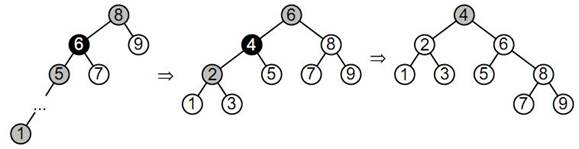
Таким образом, вместо лозы, состоящей из 15 вершин, мы получим дерево, состоящее из 7 черных вершин и 8 серых вершин (Рис.5).
Рис.5. Первое перестроение
Для второго перестроения (рис.6) сначала перекрасим серые вершины в белые. Далее перекрасим каждую вторую черную вершину в серый цвет, начиная в корне. Теперь, как и раньше, выполним малый правый поворот относительно каждой серой вершины, кроме самой нижней.
Рис.6. Второе перестроение
Третье перестроение аналогично первым двум. Вершины 12 и 4 перекрашиваются в серый цвет, затем выполняется малый правый поворот относительно вершины 12. В результате получается сбалансированное дерево.
Рис.7. Третье перестроение
Теперь необходимо разобраться со случаем, когда длина лозы не может быть представлена в виде 2n-1 для какого-либо натурального n. В этом случае необходимо привести длину главной лозы к требуемому значению. Пусть лоза состоит из m вершин. Тогда существует такое n, что (2n-1) < m < (2n+1-1). Необходимо укоротить главную лозу на m – (2n-1) вершин. После этого можно перестроить получившееся дерево аналогично способу, описанному выше. В результаты получится сбалансированное дерево с m – (2n-1) листьями. Для примера разберем случай, когда лоза состоит из 9 вершин. Отсюда следует, что n=3, т.к. (23-1)=7<9<15=(24-1). Следовательно, необходимо укоротить главную лозу на 9-(23-1)=2. После этого перестраиваем дерево аналогично примеру, приведенному выше. В результате у нас должно получиться сбалансированное дерево.
Рис.8. Сбалансированное дерево с m - (2n-1) листьями
Контрольные вопросы
1. Что означает термин «сбалансированное» дерево? 2. Для чего выполняется балансировка? 3. Опишите фазы балансировки. 4. Как происходит преобразование исходного дерева в лозу? 5. Как происходит преобразование лозы в сбалансированное дерево? 6. В каких случаях необходимо укорачивать лозу? 7. Как определить размер укорачивания? 8. Как происходит поворот относительно вершины? 9. Сколько вершин будет в сбалансированном дереве, если в исходном их 200?
Задания для практической работы
Требуется: - запрограммировать алгоритм балансировки дерева; - количество вершин лозы определяется случайно в диапазоне от 7 до 31; - каждое перестроение выводить на экран.
Глава 3. Жадные алгоритмы
Понятие жадного алгоритма Жадный алгоритм (англ. Greedy algorithm) — алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская что конечное решение также окажется оптимальным. Общего критерия оценки применимости жадного алгоритма для решения конкретной задачи не существует, однако, для задач, решаемых жадными алгоритмами характерны две особенности: во-первых, к ним применим Принцип жадного выбора; во-вторых, они обладают свойством Оптимальности для подзадач. Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных выборов даёт глобально оптимальное решение. В типичном случае доказательство оптимальности следует такой схеме: Сначала доказывается, что жадный выбор на первом шаге не закрывает пути к оптимальному решению: для всякого решения есть другое, согласованное с жадный выбором и не худшее первого. Затем показывается, что подзадача, возникающая после жадного выбора на первом шаге, аналогична исходной, и рассуждение завершается по индукции. Говорят, что задача обладает свойством оптимальности для подзадач, если оптимальное решение задачи содержит в себе оптимальные решения для всех её подзадач. Например, в задаче о выборе заявок можно заметить, что если A — оптимальный набор заявок, содержащий заявку номер 1, то Пример 1: Размен монет. Условие: Монетная система некоторого государства состоит из монет достоинством a 1 = 1 < a 2 <... < an. Требуется выдать сумму S наименьшим возможным количеством монет. Жадный алгоритм решения этой задачи таков. Берётся наибольшее возможное количество монет достоинства an: Для данной задачи жадный алгоритм не всегда даёт оптимальное решение. Например, сумму в 10 копеек монетами в 1, 5 и 6 коп. жадный алгоритм разменивает так: 6 коп. — 1 шт., 1 коп. — 4 шт., в то время как правильное решение — 2 монеты по 5 копеек. Тем не менее, на всех реальных монетных системах жадный алгоритм даёт правильный ответ.
Алгоритм Хаффмана Алгоритм Хаффмана (англ. Huffman) — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году доктором Массачусетского технологического института Дэвидом Хаффманом. Коды Хаффмана широко используются при сжатия информации (в типичной ситуации выигрыш может составить от 20% до 90% в зависимости от тина файла). Алгоритм Хаффмана находит оптимальные префиксы (коды символов), исходя из частоты использования этих символов в сжимаемом тексте, с помощью жадного выбора.
Пусть в файле длины 100 000 известны частоты символов. Мы хотим построить двоичный код, в котором каждый символ представляется в виде конечной последовательности битов, называемой кодовым словом.
Таблица 1. Коды символов
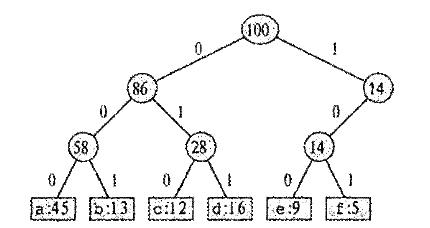
При использовании равномерного кода, в котором все кодовые слова имеют одинаковую длину, на каждый символ (из шести имеющихся) надо потратить как минимум три бита, например, а — 000, b — 001,...,f — 101 (таб.1.). На весь файл уйдет 300 000 битов.
Рис.1. Представление равномерного кода в виде дерева Неравномерный код будет экономнее, если часто встречающиеся символы закодировать короткими последовательностями битов, а редко встречающиеся длинными.
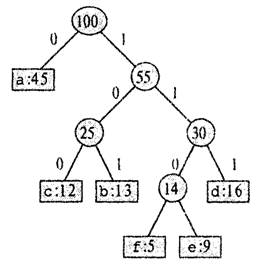
Рис.2. Представление неравномерного кода в виде дерева
. Один такой код показан на рис.2: буква а изображается однобитовой последовательностью 0, а буква f четырёхбитовой последовательностью 1 100. При такой кодировке на весь файл уйдёт (45- 1 + 13-3+ 12-3+ 16-3 + 9-1 +5-1) * 1000 = 221000 битов, что даёт около 25% экономии.
Этот метод кодирования состоит из двух основных этапов: 1. Построение оптимального кодового дерева. 2. Построение отображения код-символ на основе построенного дерева.
Общая схема построения дерева Хаффмана (рис.3): 1. Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа). 2. Из списка выберем 2 узла с наименьшим весом (под весом можно понимать частоту использования символа — чем чаще используется, тем больше весит). 3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов. 4. Добавим сформированный узел к списку. 5. Если в списке больше одного узла, то повторить 2-5.
Рис.3. Этапы построения дерева Хаффмана Контрольные вопросы 1. В чем принцип работы жадного алгоритма? 2. Какие типы задач можно решать с помощью жадного алгоритма? 3. Что понимается под методом Хаффмана? 4. Где применяется метод Хаффмана? 5. Как строится дерево Хаффмана? 6. Как вычислить размер исходного текста и сжатого? 7. Что является «префиксом»?
Задания для практической работы Задание состоит из нескольких этапов: 1. Получить у преподавателя индивидуальный текст для сжатия. 2. Создать программный модуль, который - из исходного текста получает список кодируемых символов; - Рассчитать размер несжатого файла; - С учетом полученных вероятностей, построить дерево Хаффмана; - Рассчитать размер сжатого файла. 3. Провести сравнительный анализ сжатия при разных характеристика исходного файла. Глава 4. Графы
В процессе обработки данных на компьютере часто приходится моделировать объекты сложной структуры, содержащие в качестве составных частей (элементов) объекты более простой структуры. Примерами таких структур являются— массивы, множества, списки и деревья. Иногда сложный объект состоит из некоторого множества элементов одного и того же типа, между которыми существуют определенные связи (отношения). В технике такие объекты часто называют сетями. Для моделирования сетей в математике служат объекты, называемые графами. Графом G называется пара множеств (V, E), где V— конечное множество элементов, называемых вершинами графа, а E— конечное множество упорядоченных пар е = (w, v), называемых дугами, где w, v— вершины. Говорят, что дуга е выходит из вершины w и входит в вершину v. Вершины w и v называют инцидентными дуге е, а дугу е — инцидентной вершинам w и v. В этом определении множество вершин V соответствует множеству узлов моделируемой сети, а множество дуг— связям между узлами. Определение, данное выше, отражает лишь структуру сети, но не характеристики ее отдельных узлов и связей. Если такие характеристики все же существенны, то рассматривают нагруженные графы, в которых с каждой вершиной или дугой (может быть, и с тем, и с другим) связана величина или несколько величин, называемых нагрузкой на граф. Формально говоря, нагрузку графа определяют функции: f: V->W1 g: E -> W2, где W1 и W2 представляют собой множества значений нагрузки вершин и дуг графа соответственно. Иногда при анализе графа неважно, какая из вершин w и v в дуге е = (w, v) первая, а какая вторая, т. е. пара (w, v) не упорядочена. В этом случае дугу е называют ребром, а весь граф называют неориентированным в отличие от ориентированного графа, задаваемого исходным определением. Разумеется, в этом случае бессмысленно говорить о том, из какой вершины ребро выходит и в какую вершину входит. Формально говоря, неориентированным графом называют такой граф, у которого наряду с любой дугой e1 = (u, v) имеется и противоположная дуга е2 — (v, u). Эта пара дуг и образует ребро е = <u, v> неориентированного графа.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.138 (0.055 с.) |






 — оптимальный набор заявок для меньшего множества заявок
— оптимальный набор заявок для меньшего множества заявок 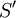 , состоящего из тех заявок, для которых
, состоящего из тех заявок, для которых 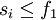 .
.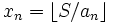 . Таким же образом получаем, сколько нужно монет меньшего номинала, и т. д.
. Таким же образом получаем, сколько нужно монет меньшего номинала, и т. д.