Поиск и включение в двоичное дерево

 

В двоичном дереве каждая вершина имеет не более двух потомков, обозначенных как левый (left) и правый (right). Кроме того, на данные, хранимые в вершинах дерева, вводится следующее правило упорядочения: значения вершин левого поддерева всегда меньше, а значения вершин правого поддерева - больше значения в текущей вершине.

struct btree {int val;btree *left,*right; }; Свойства двоичного дерева позволяют применить в нем алгоритм поиска, аналогичный двоичному поиску в массиве. Каждое сравнение искомого значения и значения в вершине позволяет выбрать для следующего шага правое или левое поддерево. Алгоритмы включения и исключения вершин дерева не должны нарушать указанное свойство: при включении вершины дерева поиск места ее размещения производится путем аналогичных сравнений. Эти алгоритмы являются линейно рекурсивными или циклическими. //----- Обход двоичного дереваvoid Scan(btree *p, int level){if (p==NULL) return;Scan(p->left,level+1);printf("l=%d val=%d\n",level,p->val);Scan(p->right,level+1); } //----- Поиск в двоичном дереве---------------                    // Возвращается указатель на найденную вершинуbtree *Search(btree *p, int v){if (p==NULL) return NULL;                          // Ветка пустаяif (p->val == v) return p;                      // Вершина найденаif (p->val > v)                             // Сравнение с текущимreturn Search(p->left,v);                       // Левое поддеревоelse return Search(p->right,v); }              // Правое поддерево //----- Включение значения в двоичное дерево--------------            // Используется ссылка на указатель на текущую вершинуvoid Insert(btree *&pp, int v){ if (pp == NULL) {                  // Найдена свободная ветка pp = new btree;                     // Создать вершину дерева pp ->val = v; pp->left = pp->right = NULL; return; }if (pp->val > v)                            // Перейти в левое илиInsert(pp->left,v);                            // правое поддеревоelse Insert(pp->right,v);} Обратите внимание, что указатель pp ссылается на то место в дереве, где находится указатель на текущую вершину, а потому под него можно производить запись (присваивание) при создании новой вершины. При замене рекурсии циклом пришлось бы довольствоваться явным двойным указателем btree **pp.

В двоичном дереве естественная нумерация вершин соответствует обходу в порядке возрастания их значений, то есть левое поддерево текущая вершина правое поддерево.

//---- Обход двоичного дерева с нумерацией вершинvoid ScanNum (btree *q, int &n) {if (q==NULL) return;ScanNum(q->left,n);printf("n=%d val=%d\n",n,q->val); n++;ScanNum(q->right,n);}

Контрольные вопросы

1. Что представляет собой двоичное дерево?
2. Чем отличается двоичное дерево от двусвязного списка?
3. В чем заключается особенность дерева как структуры данных?
4. Процедуры какого характера наиболее эффективны при работе с деревьями?
5. В чем заключается вставка узла в дерево?
6. В чем заключается удаление узла из дерева?
7. Каковы особенности удаления элемента из древовидной структуры данных?
8. В чем заключается поиск в дереве?
9. Что такое «прохождение дерева»?
10. Что такое высота дерева?
11. Как сохранить сбалансированность дерева при вставке и удалении узлов?

Задания для практической работы

Создать класс операций по работе с деревом. Программа должна содержать функцию обхода дерева с выводом его содержимого, функцию добавления вершины дерева (ввод), а также указанную в варианте функцию.

1. Вершина дерева содержит указатель на строку. Строки в дереве не упорядочены. Функция включает вершину в дерево с новой строкой в ближайшее свободное к корню дерева место. (В результате дерево будет сбалансированным). Для исключения полного обхода в каждую вершину дерева поместить длину его минимальной ветви и корректировать его в процессе включения во всех проходимых вершинах.

2. Вершина двоичного дерева содержит массив целых и два указателя на правое и левое поддерево. Массив целых в каждом элементе упорядочен, дерево в целом также упорядочено. Функция включает в дерево целую переменную с сохранением упорядоченности.

3. Вершина двоичного дерева содержит указатель на строку и указатели на правое и левое поддерево. Строки в дереве упорядочены по возрастанию. Написать функций включения строки и получения указателя на строку по заданному номеру, который она имеет в упорядоченной последовательности обхода дерева.

4. Элемент дерева содержит либо данные (строка ограниченной длины), либо указатели на правое и левое поддеревья. Строки в дереве упорядочены. Написать функцию включения новой строки. (Обратить внимание на то, что элемент с указателями не содержит данных, и при включении новой вершины вершину с данными следует заменить на вершину с указателями).

5. Вершина дерева содержит целое число и массив указателей на поддеревья. Целые в дереве не упорядочены. Функция включает вершину в дерево с новой целой переменной в ближайшее свободное к корню дерева место. (То есть дерево должно иметь ветви, отличающиеся не более чем на 1).

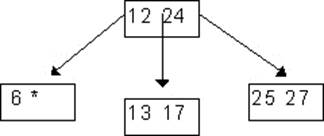
6. Вершина дерева содержит два целых числа и три указателя на поддеревья. Данные в дереве упорядочены. Написать функцию включения нового значения в дерево с сохранением упорядоченности.

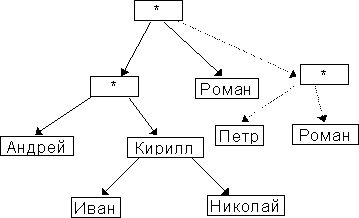
7. Вершина дерева содержит указатель на строку и N указателей на потомков. Функция помещает строки в дерево так, что строки с меньшей длиной располагаются ближе к корню. Если новая строка " проходит" через вершину, в которой находится более длинная строка, то новая занимает место старой, а алгоритм включения продолжается для старой строки. Функция включения выбирает потомка минимальным количеством вершин в поддереве.

8. Вершина дерева содержит либо 4 целых значения, либо 2 указателя на потомков, причем концевые вершины содержат данные, а промежуточные - указатели на потомков. Естественная нумерация значений производится при обходе концевых вершин слева направо. Разработать функции получения и включения значения в дерево по логическому номеру.

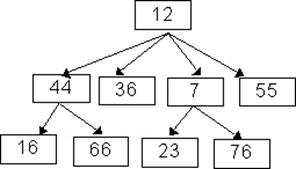
9. Вершина дерева содержит N целых значений и два указателя на потомков. Запись значений производится таким образом, что меньшие значения оказываются ближе к корню дерева (то есть все значения в поддеревьях больше самого большого значения у предка). Разработать функции включения и поиска данных в таком дереве. Если новое значение " проходит" через вершину, в которой находится большее, то оно замещает большее значение, а для последнего алгоритм включения. Функция включения выбирает потомка максимальным значением в поддереве.

10. Выражение, содержащее целые константы, арифметические операции и скобки, может быть представлено в виде двоичного дерева. Концевая вершина дерева должна содержать значение константы. Промежуточная - код операции и указатели на правый и левый операнды - вершины дерева. Функция получает строку, содержащую выражение, и строит по ней дерево. Другая функция производит вычисления по полученному дереву.

11. Вершина дерева содержит указатель на строку и динамический массив указателей на потомков. Размерность динамического массива в корневой вершине - N, на каждом следующем уровне - в 2 раза больше. Функция при включении строки создает вершину, наиболее близкую к корню.

12. Вершина дерева содержит динамический массив целых значений и два указателя на потомков. Значения в дереве не упорядочены. Размерность динамического массива в корневой вершине - N, на каждом следующем уровне - в 2 раза больше. Функция включает новое значение в свободное место в массиве ближайшей к корню вершины.

13. Вершина дерева содержит массив целых и два указателя на правое и левое поддерево. Значения в дереве не упорядочены. Естественная нумерация значений производится путем обхода дерева по принципу " левое поддерево - вершина - правое поддерево". Разработать функции включения и получения значения элемента по заданному логическому номеру.

14. Написать функцию, которая добавляет к бинарному дереву T новую вершину с элементом E (если ее не было в T).

15. Написать функцию, которая заменяет в дереве T значения всех отрицательных элементов вершин на их абсолютные величины (информационное поле вершины дерева T имеет тип Real).

16. Написать функцию, которая удаляет все вершины с одинаковыми элементами из непустого дерева T (разрешается использовать вспомогательную множественную структуру данных).

17. Написать функцию, которая удаляет из непустого бинарного дерева T вершины, содержащие максимальный и минимальный элемент (информационное поле вершины дерева имеет тип Real).

18. Написать функцию, которая удаляет из непустого дерева поиска T вершины, содержащие максимальный и минимальный элемент (информационное поле вершины дерева имеет тип Real).

19. Написать функцию, которая удаляет из непустого дерева все вершины с положительными элементами (информационное поле вершины дерева имеет тип Real).

20. Написать функцию, которая удаляет из непустого дерева поиска все вершины с отрицательными элементами (информационное поле вершины дерева имеет тип Real).

21. Написать функцию, которая определяет, входит ли вершина, содержащая информационное поле E, в заданное бинарное дерево дважды.

22. Написать функцию, которая проверяет, входит ли вершина, содержащая информационное поле E, в правое или левое поддерево заданного дерева поиска.

23. Написать функцию, которая проверяет совпадают ли элемент из самого левого листа непустого поиска дерева с элементом из самого правого листа того же дерева.

24. Установить, можно ли попасть из одной вершины бинарного дерева в другую, если двигаться по ветвям к листьям.

25. Установить, можно ли попасть из одной вершины дерева поиска в другую, если двигаться по ветвям к листьям.

26. Используя линейную скобочную запись дерева поиска, описать логическую функцию, проверяющую на равенство деревья поиска T1 и T2.

27. Написать с помощью линейной скобочной записи бинарного дерева функцию, проверяющую, входит ли вершина с элементом E в правое (левое) поддерево заданного бинарного дерева.

28. Два бинарных дерева называются изоморфными, если можно отобразить одно из них в другое, изменив порядок сыновей его узлов. Распознать изоморфизм двух данных бинарных деревьев.

29. Описать функцию, которая определяет количество вхождений вершины с заданным элементом E в бинарное дерево.

30. Описать функцию, которая вычисляет сумму элементов всех вершин заданного непустого дерева поиска (информационное поле вершины дерева имеет тип Real).

31. Описать функцию, которая определяет максимальную глубину непустого дерева, т.е. количество ветвей в самом длинном из путей от корня дерева до листьев.

32. Определить глубину (высоту) непустого дерева поиска, используя функцию определения пути от данной вершины до корня.

33. Используя линейную скобочную запись дерева, описать функцию, которая определяет максимальную глубину непустого бинарного дерева.

34. Описать функцию, которая подсчитывает количество вершин на k-ом уровне непустого дерева поиска (корень - вершина 0-го уровня).

35. Написать функцию, которая определяет количество вхождений элемента E в информационные поля вершин левого поддерева заданного бинарного дерева.

36. Написать функцию, которая вычисляет среднее арифметическое всех элементов заданного непустого дерева (информационное поле вершины дерева имеет тип Real).

37. Написать функцию, которая находит в заданном непустом бинарном дереве длину (количество ветвей) пути от корня до ближайшей вершины с заданным элементом E.

38. Определить суммарный путь данного дерева поиска, используя функцию определения пути от данной вершины до корня.

39. Используя линейную скобочную запись дерева, написать функцию, которая находит содержимое информационного поля самого левого (правого) листа непустого дерева поиска.

40. Используя линейную скобочную запись дерева, написать функцию, которая определяет количество вхождений вершины с элементом E в левое поддерево заданного бинарного дерева.

41. Используя линейную скобочную запись дерева, написать функцию, которая находит в заданном непустом бинарном дереве длину (количество ветвей) пути от корня до вершины с заданным элементом E.

42. Написать функцию, которая выбирает из непустого дерева поиска все разные английские буквы (информационное поле вершины дерева имеет тип Char).

43. Написать функцию, которая определяет максимальный элемент из всех листьев непустого бинарного дерева (информационное поле вершины дерева имеет тип Integer).

44. Написать процедуру, которая выводит на экран содержимое информационных полей всех внутренних вершин бинарного дерева.

45. Выписать все вершины дерева поиска, находящиеся на заданном уровне k (k=0,1,2,...), используя функцию определения пути от данной вершины до корня.