Определение путей и контуров Эйлера

 

Путь Эйлера проходит по каждому ребру в графе только один раз. Контур Эйлера проходит каждое ребро в графе тоже один раз, а также начинается и заканчивается в одной и той же вершине (рис. 4). Многие уже знакомы с концепцией следующей простой головоломки — нарисовать какое-то очертание без отрыва ручки от бумаги.

Если серьезно, то поиск путей и контуров Эйлера имеет более практичное применение. Их можно использовать для проложения маршрута по каким-либо реальным сетям таким образом, что каждое ребро будет проходиться в точности один раз. Существуют некоторые свойства, которыми должен обладать граф, чтобы в нем имелся путь или контур Эйлера.

Рис. 4. Граф, который имеет путь Эйлера, и сам этот путь

 

Для существования контура Эйлера каждая вершина в графе должна иметь некоторую степень. Если любая вершина имеет нечетную степень, то сформировать контур Эйлера невозможно. В каждую вершину должны входить и из нее выходить только еще не пройденные ребра. Этого никогда не случится с вершиной, имеющей нечетную степень, потому что в нее можно войти, а выйти нельзя, поскольку все выходящие ребра уже пройдены.

Чтобы получить путь Эйлера, в графе должно быть точно две вершины с нечетной степенью. Путь должен начинаться и заканчиваться в вершине с нечетной степенью, потому что только эти вершины можно посетить дополнительное (для входа) количество раз.

Теперь очевидно, что для графа требуются ограничения. Граф не должен быть связанным. Однако этот граф должен содержать только один связанный подграф. Если граф содержит больше одного связанного подграфа, то он не может иметь путей или контуров Эйлера, так как некоторые ребра никогда не будут пройдены.

Любой граф, который удовлетворяет указанным условиям, должен иметь путь Эйлера или контур Эйлера. Такой граф называется эйлеровским.

Определение пути или контура Эйлера можно провести с использованием методики, похожей на глубинный поиск. Следующий алгоритм используется для поиска контура Эйлера, но его можно немного изменить, чтобы он позволял также находить путь Эйлера в любом графе, который удовлетворяет приведенным выше условиям.

На рисунках 5—8 показан пример выполнения такого алгоритма. Работа алгоритма заключается в локализации циклов в графе с использованием похожей на глубинный поиск методики. Эти циклы затем можно скомбинировать для образования одного цикла, который проходит по всем ребрам в графе, — цикла Эйлера. Алгоритм можно описать как последовательность следующих действий:

1. Инициализировать список циклов.

2. Выполнять глубинный поиск, пока все ребра не будут удалены из графа. Добавить текущий номер вершины в текущий путь. Пройти ребро, образованное в процессе поиска, и удалить его. Если ребер для просмотра больше нет, то добавить текущий путь в список циклов, а затем продолжить поиск непройденных вершин, начиная с первой вершины.

3. Объединить пути и циклы вместе для формирования контура Эйлера.

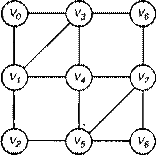
Рис. 5. Исходный граф

 

Рассмотрим подробнее этот алгоритм. Глубинный поиск начинается с вершины v0 и на последующих итерациях посещаются вершины v1 и v3. После v3 достигается v0, и полученный цикл считается найденным. Затем цикл v0, v1, v4, v3 и v0 сохраняется.

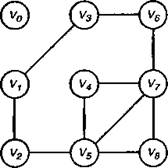
Рис 6. Ребра графа, по которым проходит

путь 0->1->4->3-> 0 удаляются

Затем глубинный поиск продолжается с первой вершины, которая имела выходящее из нее ребро. В нашем случае это вершина v,. При глубинном поиске может быть найден цикл v1, v2, v5, v4, v4, v7, v6, v3, v1 который добавляется в список циклов. Рис. 7 демонстрирует граф без второго найденного цикла.

Следующий этап глубинного поиска начинается с вершины v5; при этом обнаруживается цикл v5, v8 v7, v5. Начиная с этого момента, мы больше не найдем непросмотренных ребер. Таким образом, получилось три цикла.

Рис. 7. Граф с удаленными ребрами

по пути 1->2->5->4->7->6->3->1

Этот же алгоритм с небольшими поправками можно использовать также для поиска пути Эйлера. Разница состоит в результате первого этапа поиска. Любой граф, удовлетворяющий условиям для контура Эйлера, после первого этапа поиска создает цикл. Чтобы найти путь Эйлера, первый поиск надо провести, начиная с одной из двух вершин с нечетными степенями. Результатом такого поиска будет путь от первой вершины с нечетной степенью ко второй. Все последующие этапы поиска дают циклы, которые можно вставить в первый путь таким же образом, как и в случае с контуром Эйлера.

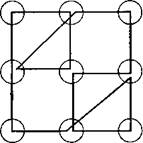
Рис. 8. Найденный контур Эйлера

 

Эффективная реализация этого алгоритма может оказаться немного громоздкой. Потенциальную проблему представляют неориентированные графы из-за обычного способа их представления. Хотя в графе ребро является единственным объектом, оно представляется как два ориентированных ребра, одно из которых идет от u к v, а другое — от v к u.

Прохождение матрицы смежности или списка смежных вершин для проверки ребер в соответствии с этим алгоритмом требует много времени. Желательно всегда передвигаться по списку ребер только вперед. Когда ребро просматривается, его можно либо удалить, либо поместить за указатель ребра этой вершины, и тогда оно больше никогда не будет просматриваться.

Это, безусловно, справедливо для ориентированных ребер; после того как ребро передается, оно больше никогда не исследуется. Неориентированные графы немного усложняют этот алгоритм, поскольку мы должны учитывать тот факт, что каждое ребро представлено в виде двух направленных ребер. Это значит, что изучить неориентированное ребро можно дважды, продвигаясь вперед и назад по каждому ребру и получая неправильные результаты.

Поиск кратчайших путей

Путем в графе называют чередующуюся последовательность вершин и дуг v1, e1, v2, e2,... vn-1 en-1, vn, в которой каждый элемент vi— вершина графа, а каждый элемент еi — дуга графа, ведущая из предыдущей вершины vi в следующую вершину vi+1|. Говорят, что такой путь соединяет вершину v1 с вершиной vn. Чаще всего рассматриваются простые пути, т. е. такие, в которых нет повторяющихся вершин, кроме, быть может, совпадения первой и последней вершины. В случае такого совпадения путь называется замкнутым или циклом.

Среди характеристик пути чаще всего рассматривается его длина— количество дуг в этом пути. Иногда с каждой дугой связывается некоторое число, которое можно интерпретировать как длину этой дуги. Граф в этом случае называется нагруженным, а длиной пути в нагруженном графе будет называться сумма длин входящих в этот путь дуг.

Самая простая задача поиска кратчайшего пути в графе состоит в следующем. Пусть заданы две вершины — начальная и конечная. Известно, что имеется по крайней мере один путь, по которому можно пройти, чтобы попасть из начальной вершины в конечную. Требуется указать один из таких путей.

Более интересная задача состоит в том, чтобы найти кратчайший путь между двумя вершинами при условии, что каждая дуга имеет определенную длину, так что мерой такого расстояния будет не количество дуг на кратчайшем пути, а суммарная длина пути.

Алгоритм Э. Дейкстры.

 

Опишем алгоритм нахождения такого пути при условии, что длины всех дуг неотрицательны. Этот алгоритм был предложен и опубликован Э. Дейкстрой (Е. W. Dijkstra), поэтому и носит его имя.

Алгоритм поиска кратчайшего пути в этом случае несколько напоминает алгоритм обхода графа в ширину и состоит в следующем. Будем рассматривать два множества: множество вершин, для которых уже известен кратчайший путь до них из начальной вершины (passed), и множество еще не исследованных вершин (notPassed).

В начале работы первое множество будет пустым, а второе будет содержать все вершины графа. На каждом шаге работы алгоритма из второго множества в первое переводится одна вершина — та, расстояние до которой от исходной вершины минимально. Эту вершину будем называть пограничной (border).

Для определения пограничной вершины во время работы алгоритма постоянно корректируется массив расстояний dist, в котором для каждой вершины хранится расстояние до нее от исходной вершины, если оно известно. В начале работы алгоритма расстояние известно только для одной вершины — начальной. Конечно, это расстояние равно нулю, так что эта вершина и будет выбрана первой в качестве пограничной. В дальнейшем массив будет корректироваться за счет просмотра вершин-кандидатов, в которые ведут дуги из очередной пограничной вершины в еще не просмотренные вершины.

Сам путь из начальной вершины в конечную будет сохраняться с помощью массива меток backs. Алгоритм заканчивает работу, как только в качестве пограничной будет выбрана конечная вершина или, если окажется, что очередная пограничная вершина вообще не связана с начальной (находится на бесконечно большом расстоянии от нее). Это расстояние задается в программе константой infinity.

Реализация этого алгоритма приведена в листинге в виде метода getDijkstraPath класса ListGraph. В качестве аргументов методу передаются номера начальной и конечной вершин на кратчайшем пути, а также переменная, которая будет содержать вектор номеров промежуточных вершин на пути из начальной вершины в конечную. Результатом работы метода будет суммарная длина кратчайшего пути.

Чтобы задать нагрузку на дуги, не изменяя представления графа, введем специальный абстрактный тип данных Graphweight, представляющий объекты, задающие нагрузку на дуги графа. Главным методом соответствующего класса будет функция arcLength, которая по заданным номерам вершин определяет длину дуги, соединяющей эти вершины. Значение функции будем считать неопределенным, если заданные вершины не соединены никакой дугой или вообще не задают номеров вершин графа. Чтобы задать конкретную нагрузку на граф, необходимо определить реализацию абстрактного типа данных GraphWeight.

 

Листинг: Алгоритм определения кратчайшего пути Э. Дейкстры с учетом длин дуг

 

double ListGraph::getDijkstraPath (int beg, int end,

const GraphWeight & weights, vector<int> & path) const

{

path.clear();

 

// Множество непросмотренных вершин:

Set notPassed(0, vertexCount()-1);

notPassed.addScale(0, vertexCount()-1);

// Массив обратных меток

int *backs = new int[vertexCount()];

// Массив минимальных расстояний. В начале работы все расстояния

// бесконечно большие, кроме расстояния до исходной вершины

 double *dist = new double[vertexCount()];

for (int i = 0; i < vertexCount(); i++)

dist[i] = INFINITY;

dist[beg] = 0;

// Цикл поиска и обработки пограничной вершины

while(!notPassed.empty()) 

{

// Поиск пограничной вершины: просматриваем массив dist

// в поисках вершины с минимальным расстоянием от beg

int border = -1;

double minDist = INFINITY;

Iterator<int> *check = notPassed.iterator();

while(check->hasMoreElements()) {

int next = **check;

if (dist[next] < minDist) { minDist = dist[border = next];

}++*check;}

delete check;

// Если пограничная вершина не найдена, то пути нет

if (border == -1) return INFINITY;

// Если пограничная вершина совпала с конечной,

// то переходим к формированию результата

if (border == end) break;

// Обработка вершин, смежных с пограничной

notPassed -= border;

Iterator<int> *nextToBorder = graph[border].iterator();

while (nextToBorder->hasMoreElements()) 

{

int v = **nextToBorder;

if (notPassed.has(v) && dist[v] >

dist[border] + weights.arcLength(border, v)) {

 backs[v] = border;

dist[v] = dist[border] + weights.arcLength(border, v);

}++*nextToBorder;}

delete nextToBorder;

}

 

// Формирование результирующего вектора

int current = end;

while(current!= beg) {

path.insert(path.begin(), current);

current = backs[current];

}

path.insert(path.begin(), beg);

return dist[end];

}

Алгоритм Флойда — Уоршалла

 

Идея алгоритмом Флойда — Уоршалла, состоит в следующем. Будем рассматривать последовательность матриц смежности. В этой матрице элемент с индексами (i,j) равен +∞, если в графе нет ребра, ведущего из вершины i в вершину j. В противном случае элемент содержит длину ребра (расстояние) от вершины i к вершине j. Имея эту начальную матрицу в качестве матрицы G0, будем получать далее последовательность матриц G1, G2,Gn, используя формулу

Gk(i,j) = min(Gk-1(i,j), Gk-1(i,k-1) + Gk-1(k -1, j)).

В этой формуле считается, что если вершины i и j не соединены дугой, то соответствующий элемент матрицы Gk(i,j) содержит бесконечно большое значение +∞, операции с которым подчиняются естественным правилам: для любого значения а (конечного или бесконечного) а + ∞ = ∞, min(a, ∞) = а.

Кроме матрицы длин кратчайших путей G надо получить еще и матрицу направлений D для того, чтобы можно было определить сами найденные кратчайшие пути. Ее можно получать сходным способом. В этой матрице элемент Dk(i,j) равен номеру начальной промежуточной вершины на кратчайшем пути из вершины i в вершину j, проходящему через промежуточные вершины из множества {0, 1,... k-1}. Ясно, что начальная матрица направлений D0 совпадает с исходной матрицей смежности графа, в которой элемент с индексами (i,j) содержит значение j, если имеется ребро, ведущее из вершины i в вершину j, и содержит -1, если такого ребра нет. В дальнейшем, при вычислении матрицы кратчайших путей, как только обнаруживается, что элемент Gk(i,j) следует заменить суммой Gk-1(i,k-1) + Gk-1(k -1, j), элемент Dk(i,j) меняется на Dk-1(i,k-1). Таким образом, в конце концов в матрице Dn будут содержаться направления по всем кратчайшим путям между всеми парами вершин в исходном графе.

Итак, имеем алгоритм, реализованный в виде функции getMinPaths. Этот метод получает в качестве аргументов исходный граф G, нагрузку на его дуги, представленную объектом класса Graphweight, и две переменные, в которые в процессе работы алгоритма и будут записаны значения элементов матрицы кратчайших путей и матрицы направлений.

Листинг: Алгоритм нахождения матрицы кратчайших путей и матрицы направлений методом Флойда — Уоршалла

void getMinPaths(const MatrixGraph & G,        // Исходный граф

const GraphWeight & w,           // Нагрузка на дуги

double ** & P,                                // Переменные для матрицы путей

int ** & D                                       //...и для матрицы направлений

) {

int n = G.vertexCount();                             // Число вершин графа

 

// Инициализация матриц.

// В матрицу длин путей записываются длины дуг исходного графа:

Р = new double*[n];

for (int i = 0; i < n; i++) {

double * row = P[i] = new double[n];

for (int j = 0; j < n; j++) { row[j] = w.arcLength(i, j);

}}

//В матрицу направлений записывается информация о направлениях

// дуг исходного графа (-1, если направление не определено):

D = new int*[n]; for (int i = 0; i < n; i++) {

int * row = D[i] = new int[n];

for (int j = 0; j < n; j++) {

row[j] = (G.hasArc(i, j)? j: -1);

}}

// Вычисление кратчайших путей и направлений

//по алгоритму Флойда — Уоршалла

for (int k = 1; k < n; k++) {

 for (int i = 0; i < n; i++) {

for (int j = 0; j < n; j++) {

if (i!= k-1 && P[i][k-1] < INFINITY && P[k-l][j] < INFINITY P[i] [j] > P[i] [k-1] + P[k-1] [j]) {

P[i][j] = P[i][k-1] + P[k-1][j];

D[i][j] = D[i][k-1];

}}}}}