
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарная теория погрешностейСодержание книги
Поиск на нашем сайте
По объективным и субъективным причинам никакие измерения нельзя выполнить абсолютно точно. Наши измерения всегда содержат те или иные погрешности, называемые также ошибками измерений. Погрешности измерений принято подразделять на три основные группы: 1. Случайные погрешности. 2. Систематические погрешности. 3. Промахи или грубые погрешности. Охарактеризуем каждую из групп подробнее. Случайные погрешности возникают в результате действия большого числа различных факторов по–разному в каждом из экспериментов. Примером случайной ошибки может служить ошибка измерения давления очень чувствительным барометром. Стрелка такого барометра отклоняется от среднего значения случайным образом. Величина отклонения зависит от того, сколько молекул и с какими скоростями соударяются с измерительной площадкой прибора в данный момент времени. Систематические погрешности возникают в результате действия различных факторов одинаковым образом в каждом из экспериментов. Эти погрешности можно подразделить на три основные подгруппы: а) погрешности известной величины или погрешности, величина которых может быть рассчитана по формуле. Такие погрешности называются поправками и могут быть устранены с помощью введения соответствующей поправки. Примеры: измерение тока прибором со сбитым на несколько делений началом отсчета; измерение времени по спешащим или отстающим часам; измерение веса тела с учетом действующей на него со стороны воздуха выталкивающей силы; б) погрешности известного происхождения, но неизвестной величины. К такому типу ошибок относятся, в частности, погрешности измерительных приборов. Они возникают вследствие трения в подвижных частях приборов и из–за деформации этих частей. Приборные ошибки обычно могут быть оценены только сверху (т. е. указывается предельная погрешность измерений такая, что реальная погрешность всегда меньше этой предельной погрешности). Для механических измерительных приборов это обычно цена минимального деления измерительной шкалы или цена деления нониуса для приборов, снабженных нониусом; для электроизмерительных приборов погрешность определяется классом точности прибора и составляет определенный процент от всего действующего значения шкалы прибора, по которой производится данное измерение;
в) погрешности неизвестного происхождения, о существовании которых экспериментатор даже и не подозревает. Например, при измерении плотности материала цилиндра экспериментатор может и не знать, что внутри цилиндра содержатся полости, и поэтому получит неправильное значение измеряемой плотности. Это один из самых коварных видов ошибок. Для их устранения надо совершенствовать методику измерений, пытаясь устранить те или иные ошибки подобного типа. Промахи или грубые погрешности возникают в результате неправильных действий экспериментатора или его ошибок. К типичным видам промахов относятся: путанье шкал приборов, похожих цифр (1 и 7, 3 и 8) при нечеткой записи. К сожалению, этот тип погрешностей наиболее часто встречается в учебной физической лаборатории. Обучающиеся чаще всего допускают следующие промахи: ошибки в арифметических вычислениях, неперевод всех единиц измерений в систему СИ, неумение оперировать с отрицательными степенями числа, неспособность различать абсолютную и относительную ошибки измерений. Ошибки прямых измерений Прямым называется измерение, выполняемое непосредственно измерительным прибором, например, длины — линейкой или силы тока — амперметром. Если в ходе прямых измерений получено n значений измеряемой величины x 1 , x 2 ,..., xn, то возникает вопрос: какое из этих значений ближе всего к истинному? Наиболее вероятно, что ближе всего к истинному — среднее арифметическое этих измерений
Его в дальнейшем мы и примем за истинное значение, поскольку само истинное значение нам неизвестно. Затем находится отклонение каждого измерения от среднего арифметического
Потом рассчитывается среднее отклонение
Далее среднее отклонение сравнивается с приборной погрешностью D x пр и в качестве окончательной ошибки прямого измерения выбирается:
Ошибка, найденная по формуле (4), называется абсолютной ошибкой прямого измерения. Для характеристики качества измерений вводят также понятие относительной ошибки
Здесь под
Типичные относительные ошибки, допускаемые в ходе лабораторного практикума, варьируются от единиц процента до примерно 20%. Окончательный результат прямого измерения записывается в виде^
Запись (7) означает, что истинное значение х лежит в интервале
В погрешности D х при записи конкретного числа оставляют одну значащую цифру, в случае, если она равна единице, сохраняют две значащие цифры. Результат следует округлить до последней значащей цифры погрешности. Если есть общий множитель в виде степени числа 10, его выносят за скобку. Например, время наступления некоторого события может быть записано в виде: t = (l,95±0,13)×103 c, при d t = 6,7%. (8) Напомним, что значащими являются любые цифры числа, кроме нулей в начале числа. В промежуточных вычислениях нужно учитывать минимум четыре значащих цифры. Ошибки косвенных измерений Косвенным называется измерение, полученное с помощью расчета по формулам. Например, объем куба можно найти по формуле V = а3, где а – ребро куба, измеряется непосредственно, а объем уже вычисляется. Пусть косвенное измерение у связано с прямым измерением x с помощью функциональной зависимости у= f (x). (9)
Рассмотрим теперь ошибки косвенных измерений в том случае, когда измеряемая величина является функцией от нескольких прямых измерений у = f (a 1,а2,...,а m). Здесь a 1, a 2,..., am прямые измерения различных физических величин. Тогда, дифференцируя у, найдем
где ∂ f/ ∂ a i – частная производная от функции f по аргументу ai. Другие аргументы при взятии частной производной по данному аргументу считаются постоянными. Заметим, что при проведении конкретных численных расчетов, учитывая точность измерений в учебной лаборатории, необходимо на каждом этапе вычислений удерживать, как минимум, четыре значащих цифры. Для косвенных измерений выводится формула относительной погрешности.
Класс точности и оценка погрешностей электрических измерений. Все электроизмерительные приборы делятся по классу точности, значения которого могут быть: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Класс точности указывает, что погрешность показаний прибора в любом месте шкалы не должна превышать 0,1%, 0,2%, 0,5%, 1,0%,1,5%, 2,5%, 4,0% соответственно. Максимальную (предельную) абсолютную погрешность прибора можно оценить по формуле:
где k – класс точности прибора; А′ – максимально возможное показание прибора на выбранной шкале. Например, абсолютная погрешность измерения напряжения в 30 В вольтметром, класс точности которого 1,0 и предел измерения 100 В (А′ = 100), составляет ΔU = 0,01∙100 = 1 В.
Относительная погрешность прибора будет тем больше, чем меньше измеряемая величина. Если, например, при помощи указанного вольтметра измерить напряжение 30 В, то относительная погрешность будет составлять:
а при измерении напряжения 10 В – 10%. При точных измерениях следует пользоваться такими приборами, чтобы предполагаемое значение измеряемой величины составляло примерно 75% от максимального значения. Чувствительностью называется величина, равная отношению углового или линейного перемещения указателя прибора к измеряемой величине, вызвавшей это перемещение, т.е.
где x – измеряемая величина; n – перемещение (число делений шкалы). Пример. Если вольтметр рассчитан на напряжение в 2,5 В и шкала прибора имеет n = 50 делений, то чувствительность прибора равна: S = 50/2,5 = 20 дел/В. Цена деления С является величиной, обратной чувствительности S:
В предыдущем примере С = 0,5 А/дел. Пределы измерений. Значение измеряемой величины, при котором стрелка прибора отклоняется до конца шкалы, называется пределом измерений этого прибора. Электроизмерительные приборы могут иметь несколько пределов измерения. Необходимо помнить, что у многопредельных приборов цена деления на различных пределах будет различна, поэтому необходимо уметь определять цену деления, которая равна значению измеряемой величины, соответствующей одному делению прибора. Пример. Амперметр с наружным шунтом имеет два предела измерений – 1,5 А и 3,0 А. Шкала имеет 150 делений. Цена деления в этих случаях будет равна 1,5:150 = 0,01 А/дел и 3,0:150 = 0,02 А/дел. По принципу действия приборы могут иметь разные конструкционные системы. Система определяется физическим явлением, которое положено в основу действия электроизмерительных приборов. Системы бывают магнитоэлектрические, электромагнитные, электродинамические, ферродинамические, индукционные, термоэлектрические, вибрационные, тепловые, детекторные, электронные, фотоэлектрические, электролитические, электростатические и др. В наших учебных лабораториях в основном применяются измерительные приборы магнитоэлектрической и электромагнитной систем. Магнитоэлектрическая система имеет условное обозначение, которое можно найти на панели прибора. Основана эта система на взаимодействии магнитного поля постоянного магнита (u– образного) и магнитного поля рамки с током. Сила этого взаимодействия прямо пропорционально зависит от силы тока в рамке, связанной со стрелочным механизмом прибора. Такая измерительная система является высокочувствительной и высокоточной, но недостатком её является подверженность внешним электромагнитным полям. Кроме того, приборы этой системы работают только в режиме постоянного тока, что обозначается на панели прибора горизонтальной прямой.
Электромагнитная система имеет условное обозначение. В этой системе вместо постоянного магнита используется электромагнит, что снижает чувствительность, точность прибора, но даёт возможность использования его и в режиме постоянного, и в режиме переменного тока, что соответствует обозначению ~. Контрольные вопросы 1. Как классифицируются ошибки физических измерений? 2. Ошибки какого типа чаще всего встречаются в учебной физической лаборатории? 3. Какие измерения называются прямыми? 4. Как определяется абсолютная погрешность прямого измерения? 5. Что такое относительная погрешность измерения? 6. Сколько значащих цифр надо оставлять в абсолютной погрешности прямого измерения? 7. Какие измерения называются косвенными? Приведите примеры. 8. Сколько значащих цифр надо удерживать в промежуточных вычислениях? РАЗДЕЛ 1. Механика
|
||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.212.203 (0.011 с.) |

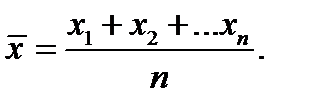 (1)
(1)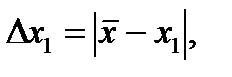
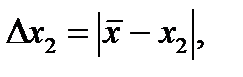 …..
….. 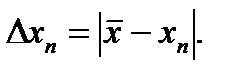 (2)
(2)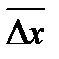
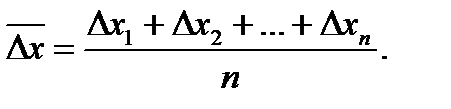 (3)
(3)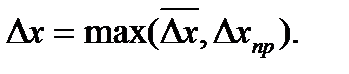 (4)
(4)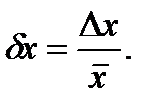 (5)
(5)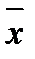 мы понимаем истинное значение измеряемой величины. Относительная ошибка часто выражается в процентах
мы понимаем истинное значение измеряемой величины. Относительная ошибка часто выражается в процентах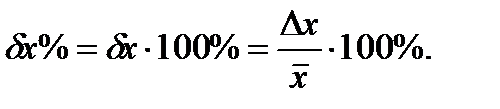 (6)
(6)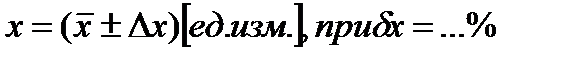 (7)
(7)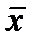 – D x £ x £
– D x £ x £ 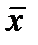 + D x. Это событие считается вероятным. Правда, само значение вероятности того, что х попадает в данный интервал, в элементарной теории погрешностей не оценивается. Существует более строгий подход к вычислению погрешностей, при котором указывается доверительный интервал, в котором лежит истинное значение и соответствующая ему доверительная вероятность. При этом необходимо принимать гипотезу о том или ином законе распределения случайной погрешности.
+ D x. Это событие считается вероятным. Правда, само значение вероятности того, что х попадает в данный интервал, в элементарной теории погрешностей не оценивается. Существует более строгий подход к вычислению погрешностей, при котором указывается доверительный интервал, в котором лежит истинное значение и соответствующая ему доверительная вероятность. При этом необходимо принимать гипотезу о том или ином законе распределения случайной погрешности.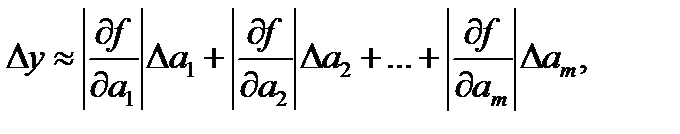 (10)
(10)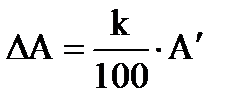 ,
,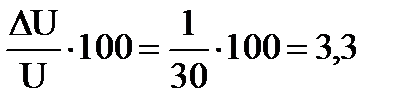 %,
%,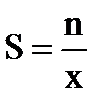 ,
,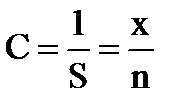 .
.


