
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выдержки из «начал» евклида и комментарииСодержание книги
Поиск на нашем сайте
В книге Евклида "Начала" математика выступала, пишет М. Клайн, "...как идеальная версия того, что составляло содержание известного нам реального мира...". Каждая книга "Начал" начинается с определений. В первой книге "Начал" приведены постулаты и аксиомы, за ними расположены в строгом порядке теоремы и задачи на построение (так, что доказательство или решение чего-либо последующего опирается на предыдущие). Там же введены 23 предварительных определения объектов геометрии: например, "точка есть то, что не имеет частей"; "линия - длина без ширины"; "прямая линия есть та, которая равно расположена по отношению к точкам на ней". Были введены определения угла, плоскости, квадрата, круга, сферы, призмы, пирамиды, пяти правильных многогранников и др. За определениями следовали 5 известных постулатов (требований) Евклида к построению фигур в геометрии: 1) От всякой точки до всякой другой точки возможно провести только одну прямую линию; 2) Ограниченную прямую линию возможно непрерывно продолжать по прямой; 3) Из всякого центра и всяким раствором возможно описать круг; 4) Все прямые углы равны между собой; 5) Если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные эти две прямые неограниченно встречаются с той стороны, где углы меньше двух прямых. Пятый постулат имеет столь важное значение, что он получил специальное наименование "пятый постулат Евклида о параллельных"[13]. Такие утверждения Евклида, как "прямая - кратчайшее расстояние между двумя точками", "через любые три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну" и постулат о параллельных были названы Кантом "априорными синтетическими суждениями" (см. Априорные синтетические суждения), являющимися частью "оснащения" нашего разума. По Г.С. Клюгелю (1763), восприятие аксиом Евклида (и в большей степени аксиомы о параллельных) как чего-то достоверного основано на человеческом опыте, ибо аксиомы опираются не столько на очевидность, сколько на опыт. А для Канта вообще был немыслим иной способ организации опыта, чем геометрия Евклида и механика Ньютона. Таким образом, со времен "Начал" Евклида и фактически до конца 19 в. законы окружающего нас физического пространства макромира были, как полагал М. Клайн, "... всего лишь теоремами геометрии Евклида и ничем больше...".
А поскольку аксиома о параллельных полностью независима от остальных, то возможно заменить ее противоположной аксиомой и выводить следствия из вновь сконструированной аксиоматической системы. Это привело к созданию неевклидовых геометрий, в которых аксиома о параллельных непротиворечиво заменяется на другую аксиому, адекватную свойствам пространства, над которым строится данная неевклидова геометрия. Хотя сочинение Евклида предназначалось для изучения физического пространства, структура самого сочинения, его остроумие и ясность изложения стимулировали аксиоматически-дедуктивный подход не только к остальным областям математики, но и ко всем естественным наукам. Через "Начала" Евклида понятие логической структуры всего физического знания, основанного на математике, стало достоянием интеллектуального мира[14]. Классическая физика имеет дело с евклидовым пространством, пространством предметов, соизмеримых с размерами человеческого тела, в котором наши органы чувств позволяют нам обходиться без усиливающих их приборов. Это пространство трехмерно, иногда двумерно. Символом его может считаться, например, число Рассмотрим круг с центром O, наложенный на многоугольник ABEFCD. Треугольник BEO прямоугольный равнобедренный, а треугольник FOC прямоугольный с углом OFC 60, а FCO 30 градусов. Считая, что площадь наложенного круга с центром O равна площади прямоугольника ABCD, требуется найти число К своему удивлению, я обнаружил, что с этой задачей незнакомы не только школьные учителя математики, но и преподаватели вузов. А задача эта примечательна тем, что в ней используются «треугольники Платона», под которыми Платон понимал прямоугольные треугольники с углами в 45, а также с углами в 60 и 30 градусов при гипотенузе. Платон считал, что на таких треугольниках держится мир.
Что дало основание Платону для такого утверждения, и почему в основу мира он клал геометрическую фигуру, а не число, как это делал, например Пифагор, которого Платон почитал? Связано это, по-видимому, с тем, что древнегреческие математики столкнулись с иррациональными числами, существование которых было неразрывно связано с треугольниками. Благодаря этому обстоятельству серьезно пошатнулась магия (натуральных) чисел, господствовавшая среди древних математиков. Да и только ли среди древних?
E F O
B OGG C O A D
Рис. 1.4. Задача Платона для вычисления числа
Не желая иметь дело с таким объектом как иррациональное число, например Роль математики Говоря о геометрии физического пространства, мы начали разговор о физике с математики. О чем это свидетельствует? Ведь физика во всех своих частях тесно переплетена с математикой, которую использует, по выражению Р. Фейнмана в качестве аппарата теоретического исследования и языка для своих рассуждений. Но дело не только в этом. Математика живет и своей самостоятельной жизнью, насколько могут быть самостоятельными отдельные науки, вносящие свой вклад в культуру общества и питающиеся его материальными и духовными ценностями. Вопрос еще и в другом: какова природа математики и что это за наука - естественная или гуманитарная. Дело в том, что когда математика с высокой точностью предсказывает физические явления, это кажется подчас чудом. Так, например, Э. Шрёдингер говорил о «господней квантовой механике», которая стала таковой в результате удачно подобранного математического аппарата, адекватно описывающего то, что происходит на самом деле. А что означает «происходить на самом деле»? Явно и по умолчанию под этим понимается в естественных науках то, что регистрируется нашими органами чувств. Даже явления микромира, не воспринимаемые невооруженным глазом, могут стать видимыми с помощью приборов. А что является критерием истинности математики? По-видимому, соответствие (иногда, впрочем, очень широко понимаемое) признанным ранее результатам и интуитивное чувство истинности.
Was fruchtbar ist, Allein ist wahr. «Лишь плодотворное верно», - писал великий Гете. А т.н. чувство истинности – откуда оно и где «проживает»? Его не найдешь в декартовом пространстве координат, хотя, казалось бы, Декарт причастен как к философии, так и к математике. Так, где же «живут» математические истины, которые вовсе не обязаны быть связанными с материей. Это уже не res extensa (вещи протяженные), а res cogitans (вещи мыслящие), согласно Декарту. Впрочем, математика здесь – не исключение. В физике истинность рассуждений существует тоже не в пространстве координат. Так зачем же физике нужна чужая епархия? Уж не сводит ли она счеты с математикой, кто главнее? Думается, что основной вопрос не в этом. Современная физика стала дорогой наукой. На ее основе выпускается самая, быть может, наукоемкая продукция – измерительная техника, компьютеры, от которых зависит будущее мировой цивилизации. Для физических исследований строятся дорогостоящие ускорители заряженных частиц, цена которых соизмерима с годовым бюджетом некоторых стран. Поэтому очень хочется знать, туда ли идем? И применить к этим оценкам количественные методы. Послушаем И. Канта: «С самых ранних времен, до которых простирается история человеческого разума, математика пошла верным путем науки у достойных удивления древних греков", "...но что касается свойственного философии способа познания из понятий в сравнении со свойственным математике способом судить a priori на основании одного лишь конструирования понятий, то обнаруживается такая глубокая разнородность философского и математического познания, которая, правда, всегда как бы чувствовалась, но никогда не была сведена к отчетливым критериям» [15]. Впрочем, о взаимоотношении физики с философией, математикой и с другими науками у нас еще будет возможность поговорить. А сейчас вернемся непосредственно к физике.
РАЗДЕЛ 2. ФИЗИКА МАКРОМИРА
3. Механическая картина мира Первая научная картина мира была построена в 18 в. трудами Коперника, Галилея, Кеплера, Ньютона и их последователей, среди которых тоже было немало выдающихся математиков. Замена небесных сфер Аристотеля кеплеровым движением планет по эллиптическим орбитам выдвинула на передний план вопрос о силах, удерживающих планеты на орбитах. Французский философ и математик Р. Декарт (1596–1650) предположил, что все пространство между телами заполнено тончайшей материей. Вихри этого вещества удерживают планеты на их орбитах, а все взаимодействия передаются путем прямого контакта.
В конце 1600-х годов в научных кругах Англии стали обсуждаться альтернативные теории тяготения. Поскольку было известно, что свет ослабляется пропорционально квадрату расстояния, несколько английских ученых, включая Э. Галлея (1656–1743), Р. Гука (1635–1702) и К. Рена (1632–1723), предположили, что могла бы существовать некая подобная сила взаимного притяжения тел. Ни один из них, однако, не дал математического решения этой проблемы. В 1684 Галлей посетил И. Ньютона (1643–1727), чтобы обсудить проблему тяготения, и, увидев, что тот близок к ее решению, настоял на ускорении работ. Следующие три года Ньютон при поддержке Галлея почти непрерывно трудился над этой проблемой. Объединив исследования Галилея над падающими на Земле телами и кеплеровы законы планетных движений, Ньютон создал строгую теорию тяготения, действительно объединившую Солнце, Землю и планеты в единую систему. Ньютон изложил свои открытия в Математических началах натуральной философии (Philosophiae naturalis principia mathematica, 1687). Все наблюдаемые в Солнечной системе явления выводились в книге Ньютона с математической точностью из нескольких основных принципов и закона всемирного тяготения. Книга I – математическое описание движения свободного тела под влиянием действующих на него сил – утверждает новые принципы механики. Она начинается с определения того, что теперь называют инерцией, массой и импульсом, а затем формулирует три знаменитых ньютоновых закона движения. Книга II – о движении тел в среде с сопротивлением – в основном опровергает теорию вихрей Декарта. В Книге III Ньютон применяет свою теорию гравитации фактически ко всем телам Солнечной системы – к планетам, Луне и другим спутникам, к кометам, – для которых имелись точные наблюдения. Неразрешимое противоречие между понятием о тяготении и действием сил на расстоянии крайне затрудняло распространение теории Ньютона. Тем не менее, в собственной стране он прошел путь от одинокого эксцентричного профессора Тринити-колледжа в Кембридже до президента Лондонского королевского общества (1703–1727). Хотя и медленно, его математические теории пускали корни. Сам Ньютон не мог объяснить особенностей движения всех членов Солнечной системы. Невозможно было точно аналитически решить задачу о движении уже трех взаимно притягивающихся тел. Даже приближенное ее решение требовало многих месяцев и даже лет кропотливых вычислений. Поколение талантливых континентальных, в первую очередь французских, математиков – таких, как Алекси Клод Клеро (1713–1765), Жан д'Аламбер (1717–1783), Леонард Эйлер (1707–1783), Жозеф Луи Лагранж (1736–1813) и Пьер Симон Лаплас (1749–1827), – успешно разрешило, в большей или меньшей степени, ряд проблем, касающихся движения тел в Солнечной системе, применяя и развивая ньютонову теорию. Кеплера законы - эмпирические законы, описывающие движение планет вокруг Солнца. Установлены И. Кеплером (J. Kepler) в нач. 17 в. на основе наблюдений положений планет относительно звёзд[16].
Первый К. з. Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце. Второй К. з. Площади, описываемые радиусами-векторами планет, пропорциональны времени. Третий К.з. Квадраты периодов обращений относятся как кубы их средних расстояний от Солнца. Первые два К. з. были опубликованы в 1609, третий - в 1619. К. з. сыграли важную роль в установлении И. Ньютоном закона всемирного тяготения. Решение задачи о движении материальной точки, взаимодействующей по этому закону с неподвижной центральной точкой (невозмущённое кеплеровское движение), приводит к формулировке обобщённых К. з. 1. В невозмущённом движении орбита движущейся точки есть кривая второго порядка, в одном из фокусов которой находится центр силы притяжения. 2. В невозмущённом движении площадь, описываемая радиусом-вектором точки, изменяется пропорционально времени. 3. В невозмущённом эллиптическом движении двух точек произведения квадратов времён обращений на суммы масс центральной и движущейся точек относятся как кубы больших полуосей их орбит:
где Т1 и Т2 - периоды обращения точек с массами m1 и m2, движущихся вокруг центральной точки с массой m0 по эллипсам с большими полуосями a1 и а2 соответственно. Третий закон, в частности, позволяет приближённо определять массы планет, обладающих спутниками. Пусть спутник с массой m2 обращается по эллипсу с большой полуосью а2 вокруг планеты с массой m1, которая, в свою очередь, движется вокруг Солнца по эллиптической орбите с большой полуосью a1. Тогда если из наблюдений известны значения a1 и а2, а также величины периодов обращений планеты вокруг Солнца (Т1) и спутника вокруг планеты (Т2), то при условии m1>m2 из третьего закона можно определить величину m1 в единицах массы Солнца m0:
Были научно объяснены формы орбит планет солнечной системы. С тех пор протяженность мира увеличилась на много порядков величины, но простота и ясность первой научной картины завораживает, Хотя в начале, надо признать, там тоже хватало забот: и внутринаучная конкуренция, и церковь…. Да и сама механика была построена логично и точно не сразу. Она все время улучшалась трудами талантливых исследователей. От уравнений Ньютона до уравнений Гамильтона прошло немало лет. Зако́ны Ньюто́на — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год)[1][2]. Первый закон Ньютона Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как Закон инерции. Инерция — это свойство тела сохранять свою скорость движения неизменной (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают разной инертностью. Инертность — это свойство тел сопротивляться изменению их скорости. Величина инертности характеризуется массой тела. Современная формулировка
Историческая формулировка Ньютон в своей книге «Математические начала натуральной философии» сформулировал первый закон механики в следующем виде:
С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета. Второй закон Ньютона Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО). Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами[4][5][6][7]. Современная формулировка
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
где Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:
где Иногда предпринимаются попытки распространить сферу применения уравнения Историческая формулировка Исходная формулировка Ньютона:
Интересно, что если добавить требование инерциальности для системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике. Третий закон Ньютона Этот закон описывает, как взаимодействуют две материальные точки. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой Современная формулировка
Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно[13]. Историческая формулировка
Уравнения Гамильтона В рамках классической механики законы природы выражаются с помощью уравнений Гамильтона: (канонические уравнения механики) - дифференциальных уравнений движения голономной механической системы[17] в канонических переменных, которыми являются s обобщённых координат qi и s обобщённых импульсов pi, где s - число степеней свободы системы. Выведены У. P. Гамильтоном (W. R. Hamilton) в 1834[18]. Для составления уравнения Гамильтона надо в качестве характеристической функции системы знать Гамильтона функцию Н(qi, рi, t), где t - время. Тогда, если все действующие на систему силы потенциальны[19], уравнения Гамильтона имеют вид
где а
где
До появления уравнений электродинамики Максвелла эти уравнения представлялись полным сводом законов природы. Начало такому подходу дал в XVIII в. Исаак Ньютон, который сформулировал его следующим образом: «Я … подозреваю, что [всякое явление природы] может быть целиком описано действием определенных сил, посредством которых частицы тел … либо притягиваются друг к другу, связываясь в правильные формы, либо отталкиваются, удаляясь друг от друга». В XIX в. физик, физиолог и психолог Герман Гельмгольц выразил подобные взгляды следующими словами: «Задачей физики является сведение всех явлений природы к силам притяжения и отталкивания, интенсивность которых зависит от расстояния между материальными телами. Только решив эту задачу, мы можем быть уверены в познаваемости природы». Явлением природы Гельмгольц считал, разумеется, и жизнь. Трудами создателей механики наблюдение и эксперимент становятся неотъемлемой частью науки. Раньше ручной труд считался уделом рабов. Теперь благодаря эксперименту и его математическому описанию стали считать, что мир состоит из взаимодействующих частиц, находящихся в непрерывном движении. Все действующие причинно-следственные связи сотворены Богом. Открывая законы функционирования мира, созданные Богом, ученые смогут предсказывать события в будущем. Появляются достаточно совершенные механические приборы: термометры, барометры, логарифмические линейки, маятниковые часы и др. Часы, подобно компьютерам в XX в., оказались причиной технологического прорыва. Правда, в древности автоматы уже применялись, особенно в Китае. Часы символизировали собой модель мира в целом. Мир считался заведенным Богом, как часы, и дальше функционировал сам по законам, Им данным. Такой подход в религии называется деизмом. Подобные взгляды были характерны для Иоганна Кеплера, Рене Декарта, Христиана Вольфа («учителя» М.В. Ломоносова) и др. Из идеи божественного предопределения родилось философское течение детерминизма и редукционизма. Ярким техническим воплощением механического подхода стала вычислительная машина, которую создал Чарльз Беббидж (1792-1871). Его машина производила вычисления быстрее человека, могла играть в шахматы, шашки и др. игры. В качестве первопричины явлений, по поводу которой И. Ньютон говорил: гипотез не делаю, выступал по-прежнему Бог. Подобная аналогия как бы заимствована из сценического оснащения античной трагедии, в которой в ходе действия мог участвовать «бог из машины», устранявший противоречия, когда они заходили так далеко, что их разрешение становилось, казалось бы, не под силу человеку. Как мы увидим из дальнейшего, наука постепенно отходила от идеи бога и уже в механистическую эпоху не кто иной, как Лаплас, отвечая Наполеону по поводу созданной им модели вселенной, заявил, что гипотеза бога ему не понадобилась. Еще Ньютон заявлял: «Гипотез не делаю». Но так ли это было на самом деле? Исследуя этот вопрос, С.И. Вавилов считал Ньютона мастером гипотез. В чем же дело? Возможно, такое утверждение понадобилось Ньютону, чтобы отмежеваться от т.н. скрытых качеств, приписываемых природе. Он предпочел сведение природных закономерностей к неким принципам. Однако, во-первых, принципы весьма напоминали гипотезы, а во-вторых, не раскрывали причин явлений, отвечая в основном на вопрос «как?», но не «почему?». В самом деле, вопрос о причине тяготения оставался и остается поныне (!) открытым. Ньютон писал: «Довольно того, что тяготение на самом деле существует и действует согласно изложенным нами законам и вполне достаточно для объяснения всех движений небесных тел и моря». Пространство и время в механике Ньютона были отделены друг от друга, т.е. существовали независимо, и рассматривались как абсолютные. И это несмотря на то, что, как было показано самим Ньютоном, никакому событию нельзя приписывать абсолютного положения в пространстве, ибо законы движения одинаковы в инерциальных системах. Но это противоречило идее абсолютного Бога, и Ньютон оставил в силе абсолютное пространство (существовавшее еще у Аристотеля), а также абсолютное время.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.11.247 (0.017 с.) |

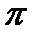 . Это число было известно древним грекам. Вот пример геометрической задачи на определение числа
. Это число было известно древним грекам. Вот пример геометрической задачи на определение числа 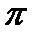 , предлагавшийся в Академии Платона.
, предлагавшийся в Академии Платона.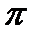 . Решение этой задачи, с которой справляются старшие школьники, я предоставляю выполнить читателям. Ответ таков:
. Решение этой задачи, с которой справляются старшие школьники, я предоставляю выполнить читателям. Ответ таков: 
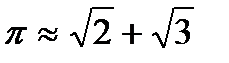 .
.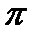
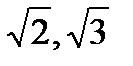 , древние стали использовать треугольники - более гармоничный объект. Однако, как мы увидим в дальнейшем, магия натуральных чисел снова вернулась в физику, когда сделали первые попытки объяснить оптические спектры химических элементов. Поскольку спектральный анализ оказался важен не только для объяснения микромира, мира атомов и молекул, но и мегамира – мира галактик. А углы между химическими связями в органических веществах и даже в молекуле воды, равно как и углы и плоскости в кристаллографии - разве это не отзвук треугольников Платона? Мы видим, таким образом, что магия чисел и треугольников не канула в Лету и оказалась достойной внимания современной науки. Поэтому не хотелось бы с порога отмахиваться от простых, кажущихся порой наивными представлений древних об устройстве природы, мира. Ведь в них - поиски единого в природе, поиски ее первоначала, от которого современная физика в некоторых своих разделах далеко ушла, но мечтает вернуться.
, древние стали использовать треугольники - более гармоничный объект. Однако, как мы увидим в дальнейшем, магия натуральных чисел снова вернулась в физику, когда сделали первые попытки объяснить оптические спектры химических элементов. Поскольку спектральный анализ оказался важен не только для объяснения микромира, мира атомов и молекул, но и мегамира – мира галактик. А углы между химическими связями в органических веществах и даже в молекуле воды, равно как и углы и плоскости в кристаллографии - разве это не отзвук треугольников Платона? Мы видим, таким образом, что магия чисел и треугольников не канула в Лету и оказалась достойной внимания современной науки. Поэтому не хотелось бы с порога отмахиваться от простых, кажущихся порой наивными представлений древних об устройстве природы, мира. Ведь в них - поиски единого в природе, поиски ее первоначала, от которого современная физика в некоторых своих разделах далеко ушла, но мечтает вернуться.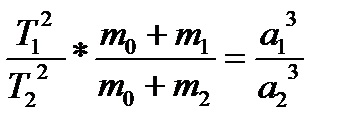 , (2.1)
, (2.1)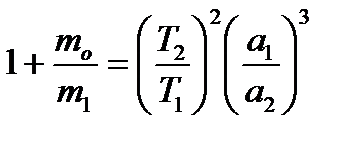 . (2.2)
. (2.2)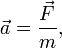
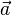 — ускорение материальной точки;
— ускорение материальной точки;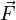 — равнодействующая всех сил, приложенных к материальной точке;
— равнодействующая всех сил, приложенных к материальной точке;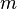 — масса материальной точки.
— масса материальной точки.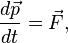
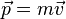 — импульс точки,
— импульс точки, 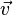 — её скорость, а
— её скорость, а 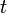 — время. При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени[8][9][10].
— время. При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени[8][9][10].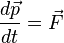 и на случай тел переменной массы. Однако, вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила [11][12].
и на случай тел переменной массы. Однако, вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила [11][12].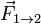 , а вторая — на первую с силой
, а вторая — на первую с силой 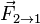 . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия
. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия 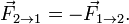
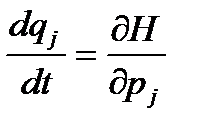 ,
, 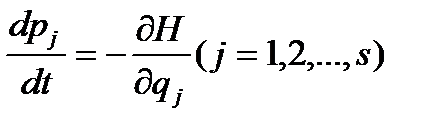 , (2.3)
, (2.3)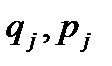 - пространственные координаты и импульсы соответственно,
- пространственные координаты и импульсы соответственно,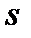 - число степеней свободы системы. Функция Гамильтона
- число степеней свободы системы. Функция Гамильтона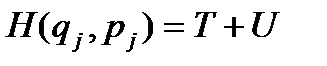 , (2.4)
, (2.4) 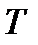 - кинетическая, а
- кинетическая, а 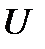 - потенциальная энергии.
- потенциальная энергии.


