
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешанные и запутанные состояния квантовых системСодержание книги
Поиск на нашем сайте
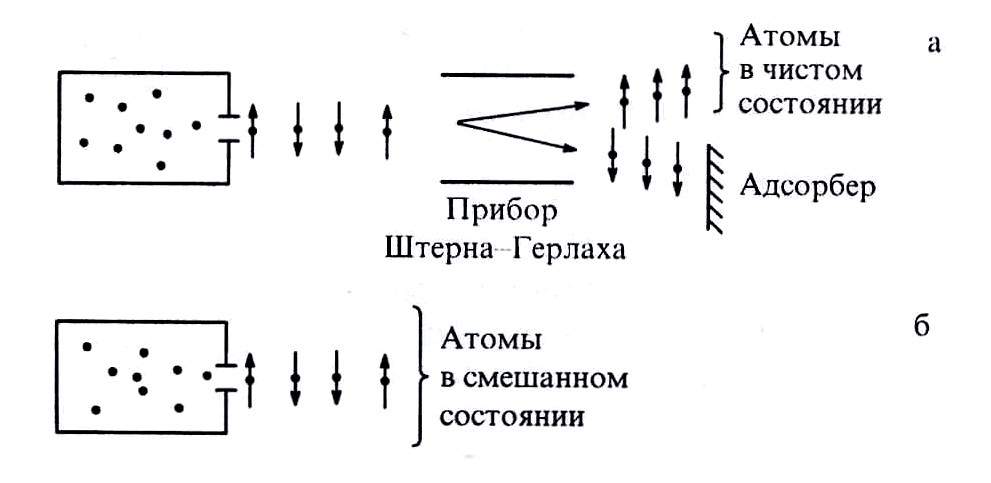
В экспериментах часто имеют дело с ансамблями квантовых систем, приготовленных определенным способом. С точки зрения описания состояния частиц в ансамбле приготовление систем можно осуществить двумя способами: 1) с получением полной информации о состоянии квантовой системы; 2) с получением только вероятностной информации о состоянии квантовой системы. Пример таких способов приготовления приведен на рис. 7.5.
Рис. 15.5. Схема приготовления атомов в чистом (а) и смешанном (б) состояниях
Печь создает поток атомов (кубитов) со спином В первом способе приготовления ансамбль атомов проходит через сепаратор (прибор Штерна-Герлаха), который пространственно разделяет его на два потока, соответствующие состояниям Математически смешанное состояние квантовой системы можно описать только матрицей плотности
Здесь
- проекторы на состояния Процессы перехода от чистых квантовых состояний к смешанным многие авторы рассматривают как процессы классицизации квантово-когерентных систем. Однако состояния, составляющие смесь, являются квантово-когерентными: в частности они могут быть запутанными, и эта запутанность может быть извлечена из смешанного состояния (entanglement purification) и передана другой квантовой системе в чистом состоянии. Процесс перехода системы от квантово-когерентного чистого состояния, описываемого волновой функцией, к некогерентному состоянию, описываемому матрицей плотности, называется также процессом декогерентизации системы.
Запутанные состояния квантовых систем Теория запутанных состояний композитных квантовых систем находится в состоянии разработки. В отношении систем, состоящих из двух частей (A и B) достигнуто более или менее полное понимание и описание запутанности. Положения теории двухчастичных систем не удается непосредственно распространить на системы, число частей которых больше двух. Для таких систем получен ряд частных результатов. Запутанность является сердцевинным свойством квантовых систем. Из существования запутанных систем вытекает нелокальность квантового описания природы. Запутанность служит важнейшим ресурсом в квантовой информатике: использование запутанных состояний обеспечивает выполнение протоколов квантовой телепортации, криптографии и вычислений. Поэтому явление запутанности вызывает большое внимание исследователей. Удивительно, что в стандартных учебниках квантовой механики о запутанности в квантовых системах даже не упоминается, хотя запутанные состояния были обнаружены ещё в 1935 г. в знаменитых работах Шрёдингера и Эйнштейна с сотрудниками. Измерение состояния кубита Измерение состояния кубитов в квантовом компьютере является одной из стандартных операций. С теоретической точки зрения нет никаких сложностей в процедуре измерения состояния кубита в базисе
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.58.83 (0.008 с.) |

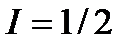 ; состояния
; состояния 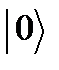 (спин вверх) и
(спин вверх) и 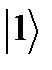 (спин вниз) встречаются в ансамбле атомов с вероятностями больцмановского распределения.
(спин вниз) встречаются в ансамбле атомов с вероятностями больцмановского распределения.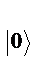 и p
и p 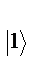 . Такое состояние представляет собой смесь чистых состояний
. Такое состояние представляет собой смесь чистых состояний 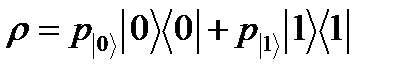 .
.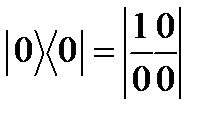 ,
, 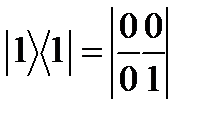
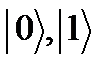 . Однако физическая реализация измерения кубита сопряжена с решением весьма сложных технологических проблем, связанных с преодолением трудностей измерения состояния отдельной атомной частицы: атома, иона, электрона, спина электрона или атомного ядра, фотона. По существу для каждой реализации кубита нужна разработка своего физического метода измерения его состояния. Можно утверждать, что проблема измерения состояния отдельных кубитов – одна из самых трудных с точки зрения физической реализации квантового компьютера.
. Однако физическая реализация измерения кубита сопряжена с решением весьма сложных технологических проблем, связанных с преодолением трудностей измерения состояния отдельной атомной частицы: атома, иона, электрона, спина электрона или атомного ядра, фотона. По существу для каждой реализации кубита нужна разработка своего физического метода измерения его состояния. Можно утверждать, что проблема измерения состояния отдельных кубитов – одна из самых трудных с точки зрения физической реализации квантового компьютера.


