Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное решение задачи КошиСодержание книги Поиск на нашем сайте
Для дифференциальных уравнений 1-го порядка
Обыкновенные дифференциальные уравнения довольно часто встречаются в различных прикладных задачах строительной механики, электротехники, исследовании разнообразных технологических процессов и поведения сложных инженерных систем. Характеристики соответствующих явлений, как правило, непрерывным образом зависят от времени и подчиняются физическим законам, которые формулируются в виде дифференциальных уравнений с начальными условиями, то есть требуют решения задачи Коши. Подавляющее большинство возникающих на практике задач такого рода невозможно решить без использования вычислительной техники. Поэтому численные методы решения задачи Коши играют в инженерных и научно-технических расчетах особую роль. Рассмотрим дифференциальное уравнение первого порядка, разрешенное относительно производной с начальным условием в точке Из теории дифференциальных уравнений известно, что если На первом этапе численного решения отрезок Следующий этап в построении численного метода состоит в замене задачи Коши ее дискретным аналогом - системой уравнений, решая которую можно последовательно найти значения
Метод Эйлера Простейший дискретный аналог дифференциального уравнения (5.1) представляет собой уравнение Геометрическая интерпретация метода Эйлера проиллюстрирована на рис.12. На каждом шаге вычислений строится касательная к интегральной кривой в точке
Рис. 12 Реализация численного алгоритма на компьютере предполагает построение алгоритма, позволяющего вычислить решение поставленной дискретной задачи Коши. В данном случае (и во всех ниже рассматриваемых случаях) вычисления производятся по явной формуле - значение сеточной функции зависит только от предыдущих значений, и программирование алгоритма не вызовет особых затруднений. Такие методы называют явными. В неявных методах правая часть уравнения может зависеть от Метод Эйлера с уточнением Приближенное решение задачи Коши методом Эйлера характеризуется очень медленной сходимостью (его погрешность убывает пропорционально лишь первой степени Метод приближенного решения задачи Коши по формулам (5.4) относится к методам класса прогноз-коррекция и иногда его называют методом Эйлера-Коши. Геометрическая иллюстрация этого метода представлена на рис.13. Если принять ломаную Эйлера в виде цепочки векторов, то значение сеточной функции по формулам (5.4) можно представить как полусумму двух последующих звеньев-векторов.
Рис.13 Как видно из рисунка, вычисленное значение гораздо находится ближе к графику искомой функции. Метод Эйлера-Коши имеет второй порядок точности, и доказательство этого факта можно найти в [1].
Методы Рунге-Кутты Наиболее популярными среди классических явных одношаговых методов являются методы Рунге-Кутты. Рассмотренные выше методы можно рассматривать как частные случаи этого класса методов. Самым известным из методов Рунге-Кутты является метод четвертого порядка точности. Вычисления на каждом шаге здесь проводятся последовательно в четыре этапа. Сначала вычисляются вспомогательные коэффициенты, а затем они подставляются в основную формулу:
Этот метод весьма прост и, как показывает практика, довольно эффективен в обычных расчетах. Литература
Приложение: Варианты контрольных работ. Вариант № 1
1. Методом половинного деления и методом хорд определить один из корней уравнения 2. Методом Гаусса найти решение системы уравнений: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами трапеций и Симпсона вычислить интеграл и сделать проверку: 5. Используя метод Эйлера 1ого порядка, составить таблицу решения дифференциального уравнения
Вариант № 2
1. Методом половинного деления и методом касательных определить один из корней уравнения 2. Методом простых итераций найти решение системы уравнений с точностью e=0,00001: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами модиф. прямоугольников и трапеций вычислить интеграл и сделать проверку: 5. Используя метод Эйлера-Коши, составить таблицу решения дифференциального уравнения
Вариант № 3
1. Методом половинного деления и методом простых итераций определить один из корней уравнения 2. Методом Зейделя найти решение системы уравнений с точностью e=0,00001: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами “правых” прямоугольников и Симпсона вычислить интеграл и сделать проверку: 5. Используя метод Рунге-Кутта, составить таблицу решения дифференциального уравнения
Вариант № 4
1. Методом половинного деления и методом хорд определить один из корней уравнения 2. Методом простых итераций найти решение системы уравнений с точностью e=0,00001: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами трапеций и “левых” прямоугольников вычислить интеграл и сделать проверку: 5. Используя метод Эйлера-Коши, составить таблицу решения дифференциального уравнения
Вариант № 5
1. Методом половинного деления и методом касательных определить один из корней уравнения
2. Методом Гаусса найти решение системы уравнений:
3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами Симпсона и трапеций вычислить интеграл и сделать проверку: 5. Используя метод Рунге-Кутта, составить таблицу решения дифференциального уравнения
Вариант № 6
1. Методом половинного деления и методом простых итераций определить один из корней уравнения 2. Методом Зейделя найти решение системы уравнений с точностью e=0,00001: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами “левых” прямоугольников и Симпсона вычислить интеграл и сделать проверку: 5. Используя метод Эйлера 1 ого порядка, составить таблицу решения дифференциального уравнения
Вариант № 7
1. Методом половинного деления и методом простых итераций определить один из корней уравнения 2. Методом Гаусса найти решение системы уравнений: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами трапеций и Симпсона вычислить интеграл и сделать проверку: 5. Используя метод Эйлера-Коши, составить таблицу решения дифференциального уравнения
Вариант № 8
1. Методом половинного деления и методом касательных определить один из корней уравнения 2. Методом Гаусса найти решение системы уравнений: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами Симпсона и трапеций вычислить интеграл и сделать проверку: 5. Используя метод Рунге-Кутта, составить таблицу решения дифференциального уравнения
Вариант № 9
1. Методом половинного деления и методом простых итераций определить один из корней уравнения 2. Методом Зейделя найти решение системы уравнений с точностью e=0,00001: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами “левых” прямоугольников и Симпсона вычислить интеграл и сделать проверку: 5. Используя метод Эйлера 1 ого порядка, составить таблицу решения дифференциального уравнения
Вариант № 10
1. Методом половинного деления и методом хорд определить один из корней уравнения 2. Методом простых итераций найти решение системы уравнений с точностью e=0,00001: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами трапеций и “левых” прямоугольников вычислить интеграл и сделать проверку: 5. Используя метод Эйлера-Коши, составить таблицу решения дифференциального уравнения
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 97; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.255.103 (0.008 с.) |

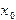 :
: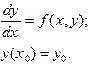 (5.1)
(5.1)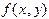 и
и 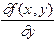 непрерывны в окрестности точки
непрерывны в окрестности точки 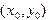 , то в этой окрестности существует, и единственное, решение задачи Коши (5.1).
, то в этой окрестности существует, и единственное, решение задачи Коши (5.1).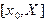 области непрерывного изменения аргумента заменяется набором дискретных точек
области непрерывного изменения аргумента заменяется набором дискретных точек 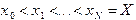 , который называется сеткой. Сами точки
, который называется сеткой. Сами точки 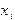 называются узлами сетки, а величина
называются узлами сетки, а величина 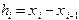 - шагом сетки. Мы будем рассматривать такие сетки, у которых шаг постоянен, тогда
- шагом сетки. Мы будем рассматривать такие сетки, у которых шаг постоянен, тогда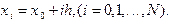 (5.2)
(5.2)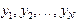 сеточной функции
сеточной функции 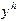 , играющие роль приближений к значениям решения задачи Коши в узлах сетки.
, играющие роль приближений к значениям решения задачи Коши в узлах сетки. ,
,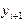 осуществляется здесь по формуле
осуществляется здесь по формуле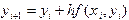 . (5.3)
. (5.3)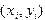 , и за
, и за 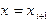 . В результате неизвестная интегральная кривая заменяется ломаной линией, называемой ломаной Эйлера.
. В результате неизвестная интегральная кривая заменяется ломаной линией, называемой ломаной Эйлера.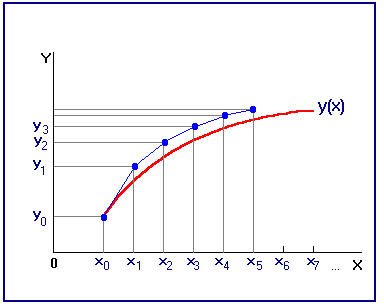
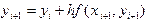 .
.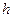 ). Это является серьезным препятствием для использования его на практике. Однако расчетные формулы можно подправить, чтобы увеличить точность вычислений. Рассмотрим следующую модификацию метода Эйлера. На первом этапе по формуле (5.3) вычисляется начальное приближение к
). Это является серьезным препятствием для использования его на практике. Однако расчетные формулы можно подправить, чтобы увеличить точность вычислений. Рассмотрим следующую модификацию метода Эйлера. На первом этапе по формуле (5.3) вычисляется начальное приближение к 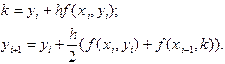 (5.4)
(5.4)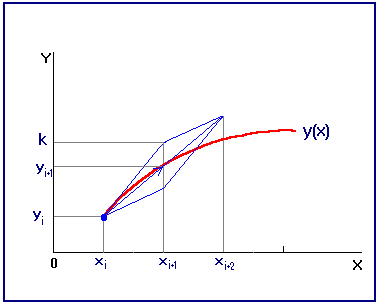
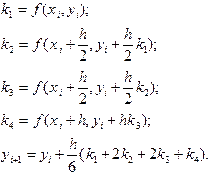 (5.5)
(5.5)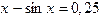 с точностью до e=0,0001
с точностью до e=0,0001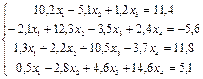
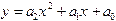
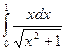
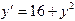 с начальным условием
с начальным условием 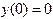 и шагом
и шагом 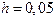 на отрезке
на отрезке 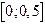
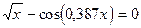 с точностью до e=0,0001
с точностью до e=0,0001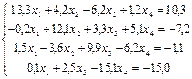
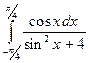
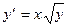 с начальным условием
с начальным условием 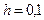 на отрезке
на отрезке 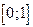
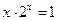 с точностью до e=0,0001
с точностью до e=0,0001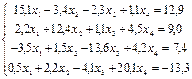
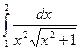
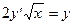 с начальным условием
с начальным условием 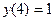 и шагом
и шагом 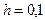 на отрезке
на отрезке 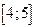
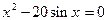 с точностью до e=0,00001
с точностью до e=0,00001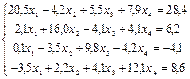
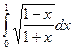
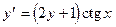 с начальным условием
с начальным условием 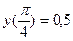 и шагом
и шагом 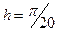 на отрезке
на отрезке 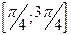
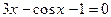 с точностью до e=0,0001
с точностью до e=0,0001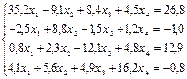
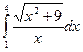
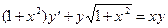 с начальным условием
с начальным условием 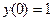 и шагом
и шагом 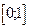
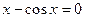 с точностью до e=0,0001
с точностью до e=0,0001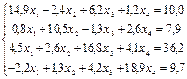
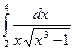
 с начальным условием
с начальным условием 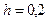 на отрезке
на отрезке 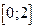
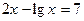 с точностью до e=0,00001
с точностью до e=0,00001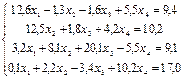
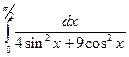
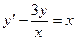 с начальным условием
с начальным условием 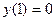 и шагом
и шагом 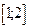
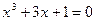 с точностью до e=0,0001
с точностью до e=0,0001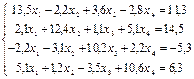
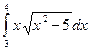
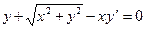 с начальным условием
с начальным условием 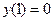 и шагом
и шагом 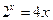 с точностью до e=0,0001
с точностью до e=0,0001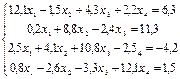
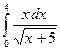
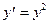 с начальным условием
с начальным условием 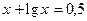 с точностью до e=0,00001
с точностью до e=0,00001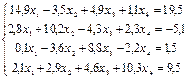
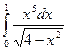
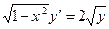 с начальным условием
с начальным условием 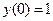 и шагом
и шагом 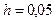 на отрезке
на отрезке