
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип наименьших квадратов
В отличие от задач интерполяции, аппроксимация по методу наименьших квадратов не требует выполнения условия (3.2) совпадения функций Пусть функция
Рис.6 Предположим, что для аппроксимации функции используется многочлен Пусть Эта величина, как видно из формулы, представляет собой сумму квадратов отклонений аппроксимирующего многочлена от табличных значений. Как известно из курса дифференциального исчисления, такая функция многих переменных в точке экстремума (минимума) должна иметь частные производные по всем переменным, равные нулю:
Линейная аппроксимация Ставится задача найти коэффициенты аппроксимирующего многочлена, если предположить, что он имеет линейный вид:
Эта система может быть записана в виде где Таким образом, вычисляя по этим формулам значения коэффициентов системы и свободных членов, можно найти затем ее решение каким-либо известным методом. Остается лишь запрограммировать формулы (3.7) перед тем, как воспользоваться стандартной процедурой решения систем линейных уравнений, описанной раньше, например. В результате будут найдены значения коэффициентов Квадратичная аппроксимация Аналогично решается задача нахождения коэффициентов аппроксимирующего многочлена 2-го порядка. В этом случае он имеет вид где Как видно из формул (3.8), полученная система симметрична и хорошо решается методом Гаусса, не требуя выбора главных элементов. Однако для многочленов более высокой степени ( Замечание 1. В том случае, когда m=n, найденный методом наименьших квадратов аппроксимирующий многочлен совпадает с интерполяционным многочленом. При этом минимизируемая функция Замечание 2. Как правило, при использовании метода наименьших квадратов предполагается, что
Численное интегрирование
В прикладных исследованиях часто возникает необходимость вычисления определенных интегралов
Определение: квадратурной формулой называется приближенное равенство вида где
Ниже рассматриваются некоторые широко распространенные простые квадратурные формулы. Все они основаны на геометрических представлениях. Будем интерпретировать интеграл как площадь криволинейной трапеции, ограниченной графиком функции
Рис.7
Разобьем отрезок Формулы прямоугольников Заменим приближенно площадь элементарной криволинейной трапеции площадью прямоугольника, основанием которого является отрезок
Рис.8
Если взять за высоту прямоугольника значение Во втором случае Наконец, если за высоту прямоугольника брать значение функции Названия формул (4.2) и (4.3) следуют из геометрической иллюстрации (рис.8). В соответствии с этим приближенное равенство (4.4) иногда называют формулой центральных прямоугольников. Ниже, когда будут рассматриваться вопросы о точности квадратурных формул, выяснится, что она точнее на порядок по сравнению с (4.2) и (4.3). По этой причине для численного интегрирования гораздо чаще применяют (4.4) и называют ее просто формулой прямоугольников. Для всех трех полученных формул их применение означает приближенную замену площади исходной криволинейной трапеции площадью ступенчатой фигуры, состоящей из элементарных прямоугольников (рис.9 - для формулы центральных прямоугольников).
Рис.9 Формула трапеций Соединив отрезком точки
Эта формула соответствует приближенной замене площади исходной криволинейной трапеции площадью фигуры, ограниченной ломаной линией, проходящей через точки
Рис. 10 Рис. 11
Формула Симпсона (парабол) Если площадь элементарной криволинейной трапеции заменить площадью фигуры, расположенной под параболой, проходящей через точки
Интегрирование полученного выражения на элементарном отрезке приводит к равенству
Таким образом, получена элементарная квадратурная формула Симпсона. Применяя эту формулу и суммируя результаты для всего отрезка интегрирования, выводим составную квадратурную формулу Симпсона:
Замечание 1. Учитывая геометрическую интерпретацию формулы Симпсона, ее иногда называют формулой парабол. Замечание 2. В случае, когда число элементарных отрезков разбиения четно ( Эта формула легко вытекает из (4.6), если при выводе принять Оценка погрешности Итак, полученные формулы (4.2)-(4.7) позволяют приближенно вычислять определенные интегралы. Программирование здесь сводится к тривиальному использованию операторов цикла для вычисления сумм, поэтому нет необходимости приводить здесь тексты программ. Другой важный вопрос - в каких случаях применять ту или иную формулу - связан с погрешностью вычислений.
Оценим погрешность выведенных квадратурных формул. Будем использовать обозначение Пусть функция Так как В точности такая же оценка погрешности справедлива и для формулы правых прямоугольников. Ее можно получить, проведя аналогичные выкладки при разложении функции по формуле Тейлора в окрестности точки Подобным же способом оцениваются погрешности других квадратурных формул. Справедливы следующие утверждения (без доказательства):
Пусть функция а для формулы трапеций: Приведенные оценки показывают, что формулы (4.2) и (4.3) имеют лишь первый порядок точности относительно Замечание3. Из оценок (4.9)-(4.11) следует, что формулы прямоугольников и трапеций точны для многочленов первой степени, а формула Симпсона - для многочленов четвертой степени. Замечание4. При вычислении интегралов по приведенным выше квадратурным формулам необходимо учитывать тот фактор, что при увеличении числа узлов возрастает влияние ошибок округления, поэтому для повышения точности рекомендуется не столько увеличивать это число, сколько применять более точную формулу.
|
||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 69; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.28.197 (0.049 с.) |
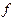 и
и 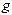 в узловых точках. Такая задача возникает в самых различных областях науки и техники, например, при обработке экспериментальных данных.
в узловых точках. Такая задача возникает в самых различных областях науки и техники, например, при обработке экспериментальных данных.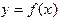 задана таблицей приближенных значений:
задана таблицей приближенных значений: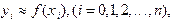 (3.3) полученных из эксперимента с ошибками
(3.3) полученных из эксперимента с ошибками 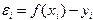 . Такие ошибки могут носить случайный характер и зачастую уровень погрешности бывает значительным (на рис.6,б показан пример графика ”истинной” функции
. Такие ошибки могут носить случайный характер и зачастую уровень погрешности бывает значительным (на рис.6,б показан пример графика ”истинной” функции 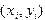 - данными эксперимента).
- данными эксперимента).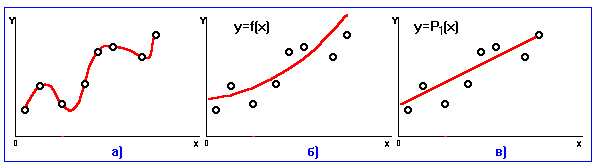
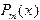 степени
степени 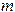 . Если применять метод интерполяции, то тогда необходимо, чтобы выполнялось условие
. Если применять метод интерполяции, то тогда необходимо, чтобы выполнялось условие 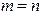 . В этом случае график функции пройдет точно через точки
. В этом случае график функции пройдет точно через точки 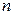 степень многочлена слишком велика, а это может привести к значительным вычислительным погрешностям.
степень многочлена слишком велика, а это может привести к значительным вычислительным погрешностям.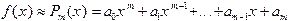 . Из различных критериев, позволяющих выбрать параметры
. Из различных критериев, позволяющих выбрать параметры 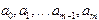 так, чтобы приближенное равенство удовлетворялось наилучшим образом, наиболее часто используют принцип наименьших квадратов. Согласно этому критерию параметры выбирают так, чтобы минимизировать величину
так, чтобы приближенное равенство удовлетворялось наилучшим образом, наиболее часто используют принцип наименьших квадратов. Согласно этому критерию параметры выбирают так, чтобы минимизировать величину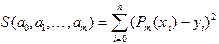 . (3.4)
. (3.4)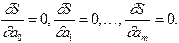 (3.5)
(3.5)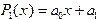 . Тогда минимизируемая функция - функция двух переменных
. Тогда минимизируемая функция - функция двух переменных  , и для нахождения наилучших по принципу наименьших квадратов коэффициентов получаем систему двух линейных алгебраических уравнений с двумя неизвестными:
, и для нахождения наилучших по принципу наименьших квадратов коэффициентов получаем систему двух линейных алгебраических уравнений с двумя неизвестными: . (3.6)
. (3.6) ,
, ,
, 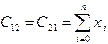 ,
,  ,
, 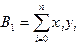 ,
, 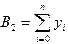 . (3.7)
. (3.7)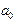 и
и 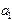 , а график искомой функции будет представлять собой прямую и может выглядеть, например, как на рис.6,в.
, а график искомой функции будет представлять собой прямую и может выглядеть, например, как на рис.6,в.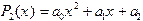 и график представляет собой параболу. Минимизируемая функция - функция трех переменных
и график представляет собой параболу. Минимизируемая функция - функция трех переменных 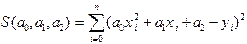 . Повторяя те же выкладки, что и в предыдущем разделе, можно прийти к системе трех уравнений с тремя неизвестными (проделайте их самостоятельно):
. Повторяя те же выкладки, что и в предыдущем разделе, можно прийти к системе трех уравнений с тремя неизвестными (проделайте их самостоятельно):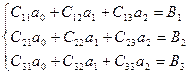 ,
, ,
,  ,
, 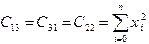 ,
, 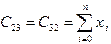 ,
,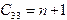 ,
, 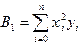 ,
,  ,
,  . (3.8)
. (3.8)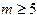 ) использование такого метода не рекомендуется, так как вычисленные на ЭВМ параметры могут оказаться полностью искаженными ошибками округления.
) использование такого метода не рекомендуется, так как вычисленные на ЭВМ параметры могут оказаться полностью искаженными ошибками округления.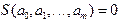 , и значения многочлена в узловых точках совпадают с табличными значениями.
, и значения многочлена в узловых точках совпадают с табличными значениями. . В этом случае метод обладает некоторыми сглаживающими свойствами.
. В этом случае метод обладает некоторыми сглаживающими свойствами.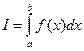 . К сожалению, в подавляющем большинстве случаев получить значение такого интеграла известными аналитическими методами не удается. Например, интеграл
. К сожалению, в подавляющем большинстве случаев получить значение такого интеграла известными аналитическими методами не удается. Например, интеграл 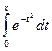 широко используется при исследовании процессов теплообмена и диффузии, в статистической физике и теории вероятностей. Однако его значение не может быть выражено в виде конечной комбинации элементарных функций. В других случаях окончательный результат выражается чрезмерно громоздкой формулой, неудобной для дальнейших вычислений. Иногда подынтегральная функция задана таблично, и точное значение интеграла получить невозможно. Тогда применяют специальные методы численного интегрирования.
широко используется при исследовании процессов теплообмена и диффузии, в статистической физике и теории вероятностей. Однако его значение не может быть выражено в виде конечной комбинации элементарных функций. В других случаях окончательный результат выражается чрезмерно громоздкой формулой, неудобной для дальнейших вычислений. Иногда подынтегральная функция задана таблично, и точное значение интеграла получить невозможно. Тогда применяют специальные методы численного интегрирования. , (4.1)
, (4.1) - некоторые точки из отрезка
- некоторые точки из отрезка 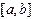 , называемые узлами, а
, называемые узлами, а  - числовые коэффициенты, называемые весами квадратурной формулы. Величина
- числовые коэффициенты, называемые весами квадратурной формулы. Величина 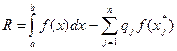 называется погрешностью (или остаточным членом) квадратурной формулы.
называется погрешностью (или остаточным членом) квадратурной формулы.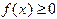 ), осью абсцисс и прямыми
), осью абсцисс и прямыми 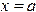 и
и  (рис.7).
(рис.7).
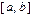 на элементарные отрезки
на элементарные отрезки  точками
точками 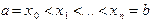 . Интеграл разобьется при этом на сумму элементарных интегралов
. Интеграл разобьется при этом на сумму элементарных интегралов 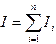 , где
, где  , что соответствует разбиению площади исходной криволинейной трапеции на сумму площадей элементарных криволинейных трапеций (рис.7). Введем обозначения:
, что соответствует разбиению площади исходной криволинейной трапеции на сумму площадей элементарных криволинейных трапеций (рис.7). Введем обозначения: 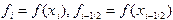 , где
, где 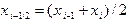 - середина элементарного отрезка. Для простоты шаг
- середина элементарного отрезка. Для простоты шаг 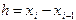 будем считать постоянным (
будем считать постоянным ( ).
). , а высота равна либо
, а высота равна либо  (рис.8,а), либо
(рис.8,а), либо  (рис.8,б), либо
(рис.8,б), либо  (рис.8,в).
(рис.8,в).
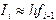 , тогда, суммируя все элементарные площади, получаем квадратурную формулу левых прямоугольников:
, тогда, суммируя все элементарные площади, получаем квадратурную формулу левых прямоугольников: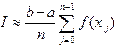 . (4.2)
. (4.2) , и тогда приходим к квадратурной формуле правых прямоугольников:
, и тогда приходим к квадратурной формуле правых прямоугольников: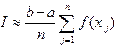 . (4.3)
. (4.3)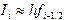 , а составная формула выглядит как
, а составная формула выглядит как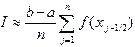 . (4.4)
. (4.4)
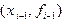 и
и  на графике функции
на графике функции 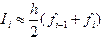 . Пользуясь этой формулой для каждой элементарной трапеции и суммируя их площади, получим составную квадратурную формулу трапеций:
. Пользуясь этой формулой для каждой элементарной трапеции и суммируя их площади, получим составную квадратурную формулу трапеций: . (4.5)
. (4.5)

 и
и  . Здесь
. Здесь 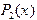 - интерполяционный многочлен 2-й степени с узлами
- интерполяционный многочлен 2-й степени с узлами 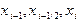 . На рис.11 показана такая парабола, а график функции
. На рис.11 показана такая парабола, а график функции 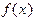 на элементарном отрезке для большей наглядности изображен искривленным. Если построить интерполяционный многочлен по указанным трем точкам, он будет выражаться формулой
на элементарном отрезке для большей наглядности изображен искривленным. Если построить интерполяционный многочлен по указанным трем точкам, он будет выражаться формулой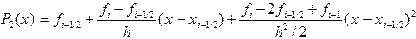 .
.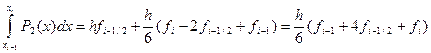 .
.  (4.6)
(4.6)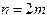 ), в формуле Симпсона можно использовать узлы лишь с целыми индексами:
), в формуле Симпсона можно использовать узлы лишь с целыми индексами: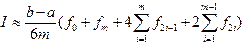 (4.7)
(4.7)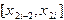 за элементарный отрезок длины
за элементарный отрезок длины  .
.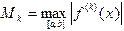 - максимальное значение производной
- максимальное значение производной 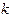 -го порядка от подынтегральной функции на отрезке
-го порядка от подынтегральной функции на отрезке  .
. , где
, где  , имеем
, имеем 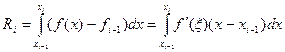 , и тогда
, и тогда .
. , то, заменяя
, то, заменяя 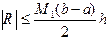 . (4.8)
. (4.8)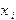 .
.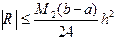 , (4.9)
, (4.9)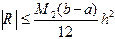 . (4.10)
. (4.10)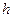 , поэтому они используются крайне редко. Предпочтительнее использование формул (4.4) и (4.5), которые имеют второй порядок точности. Однако вычисление интегралов по формуле Симпсона дает четвертый порядок точности относительно
, поэтому они используются крайне редко. Предпочтительнее использование формул (4.4) и (4.5), которые имеют второй порядок точности. Однако вычисление интегралов по формуле Симпсона дает четвертый порядок точности относительно  . (4.11)
. (4.11)


